Haar wavelet transform
Wavelets provide an elegant technique for representing functions hierarchically. They allow a function to be described in terms of a coarse overall shape, plus details that range from broad to narrow.
基础知识
向量空间:
定义在 F F F域上的向量空间是指一个 V V V集合和满足以下公理的二元运算, V V V的元素称为向量, F F F的元素称为标量。
1. 一维简单图片如何用小波进行分解——小波变换
我们将从一个简单的例子开始,使得大家对小波工作原理有一个直观的感受。假设我们有一个一维的只有4个像素值的图片,它的值是
9
7
3
5
9\ 7\ 3\ 5
9 7 3 5
我们通过小波变换将(1)图片用 Haar 基来表示。小波变换很简单:将像素值两两成对求平均得到一个更低分辨率的图像(两个像素值)
8
4
8\ 4
8 4
很显然,在这个平均化的过程中,一些信息势必会损失掉。为了能够使用(2)的信息来还原(1),我们还必须掌握一些弥补丢失信息的细节系数。在这个例子中,第一个细节系数我们选择
1
1
1,因为(1)中前两个像素值
9
,
7
9,7
9,7的平均值为(2)中的
8
8
8,它比
9
9
9少
1
1
1,比7多
1
1
1;同理第二个细节系数应该是
−
1
-1
−1,因为
4
+
(
−
1
)
=
3
,
4
−
(
−
1
)
=
5
4 + (-1) = 3, 4 - (-1) = 5
4+(−1)=3,4−(−1)=5。
至此,我们就已经完成了将一个4像素值的原始图片分解为一个更低维度的图片以及一组细节系数。重复这个过程可以得到全分解,如下表

最后,我们就可以得出原始图像(1)的小波变换,它是由代表原始图像整体平均值的单个系数和以分辨率递增排序的细节系数组成。因此,在我们的例子中,(1)的小波变换为
6
2
1
−
1
6\ 2\ 1\ -1
6 2 1 −1
2. 一维 Haar 小波基函数
一维的图像可以被看作是一系列系数。同样的,我们也可以把图像看作是在区间 [ 0 , 1 ) [0, 1) [0,1) 上的分段函数。
向量空间:
V 0 V^0 V0 : 在 1 1 1 像素图片里,它的向量空间中只有一个函数,即
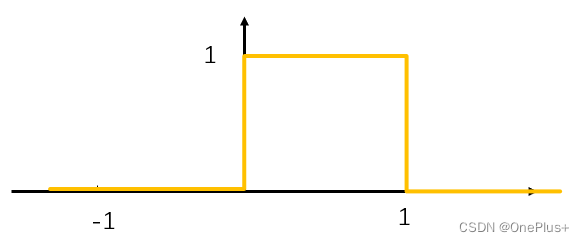
V 1 V^1 V1:在 2 2 2 像素图片中,它的向量空间中包含两个函数,为

以此类推,在包含 2 j 2^j 2j 个像素的图片里,包含 2 j 2^j 2j个类似分段函数,其向量空间记为 V j V^j Vj。因此每一个带有 2 j 2^j 2j 个像素的图片实例就是 V j V^j Vj空间的一个向量。
可以看出 V 0 ⊂ V 1 ⊂ ⋯ ⊂ V j V^0 \subset V^1 \subset \cdots \subset V^j V0⊂V1⊂⋯⊂Vj。
Haar Scaling function
向量空间的基:
向量空间
V
j
V^j
Vj 的基函数也被叫做 scaling functions,常用
ϕ
\phi
ϕ 表示。
V
j
V^j
Vj 的一个很简单的基函数可以这样定义
ϕ
i
j
(
x
)
:
=
ϕ
(
2
j
x
−
i
)
,
i
=
0
,
1
,
⋯
,
2
j
−
1
w
h
e
r
e
,
ϕ
(
x
)
:
=
{
1
,
for
0
≤
x
<
1
0
,
otherwise
\phi^j_i(x):=\phi(2^j x - i), i=0, 1, \cdots, 2^j - 1 \\ where, \\ \phi(x):= \begin{cases} 1, & \text { for } 0 \leq x<1 \\ 0, & \text { otherwise } \end{cases}
ϕij(x):=ϕ(2jx−i),i=0,1,⋯,2j−1where,ϕ(x):={1,0, for 0≤x<1 otherwise
例如在
V
2
V^2
V2 空间中,
ϕ
\phi
ϕ 分为以下4种情况:

Haar wavelet
向量空间的内积:
在
V
j
V^j
Vj 空间中任意两个向量
f
,
g
f, g
f,g 的内积为
⟨
f
∣
g
⟩
:
=
∫
0
1
f
(
x
)
g
(
x
)
d
x
\langle f \mid g\rangle:=\int_0^1 f(x) g(x) d x
⟨f∣g⟩:=∫01f(x)g(x)dx
定义
W
j
W^j
Wj 为
V
j
+
1
V^{j+1}
Vj+1 中
V
j
V^j
Vj 的一个正交子空间,即
W
j
W^j
Wj 中的每一个向量都与
V
j
V^j
Vj 中的任意向量正交(也就是内积为零)。大体上,我们可以将
W
j
W^j
Wj 看作是
V
j
+
1
V^{j+1}
Vj+1 中无法用
V
j
V^j
Vj 所刻画的那些细节。
而生成 W j W^j Wj 的那些线性独立的函数基 ψ i j ( x ) \psi^j_i(x) ψij(x) 则被称为小波。他们具有以下两个性质:
- W j W^j Wj 的基函数 ψ i j \psi^j_i ψij 与 V j V^j Vj 的基函数 ϕ i j \phi^j_i ϕij 共同构成了 V j + 1 V^{j+1} Vj+1 的基;
- 每一个基函数 ψ j \psi^j ψj 都与 任意一个基函数 ϕ j \phi^j ϕj 正交。
因此,之前说的细节系数其实就是小波函数的系数。
Haar 小波定义为
ψ
i
j
(
x
)
:
=
ψ
(
2
j
x
−
1
)
,
i
=
0
,
1
,
⋯
,
2
j
−
1
w
h
e
r
e
,
ψ
(
x
)
=
{
1
for
0
≤
x
<
1
2
−
1
for
1
2
≤
x
<
1
0
otherwise
\psi^j_i(x):= \psi(2^j x - 1), i=0,1,\cdots,2^j-1\\ where,\\ \psi(x) = \begin{cases} 1 & \text{ for } 0 \le x <\frac{1}{2} \\ -1 & \text{ for } \frac{1}{2} \le x < 1\\ 0 & \text{ otherwise } \end{cases}
ψij(x):=ψ(2jx−1),i=0,1,⋯,2j−1where,ψ(x)=⎩⎪⎨⎪⎧1−10 for 0≤x<21 for 21≤x<1 otherwise
例如
W
1
W^1
W1 空间的小波基函数
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GMYUPLmh-1669963977408)(C:\Users\BaoJinzhou\AppData\Roaming\Typora\typora-user-images\image-20221020172544784.png)]](https://i-blog.csdnimg.cn/blog_migrate/8575afebfecdb2557eac99d4165b034d.png)
3. 重新分析一维图像
原始图像是
2
2
2^2
22 空间中的一个向量,可以这样表示
I
(
x
)
=
c
0
2
ϕ
0
2
(
x
)
+
c
1
2
ϕ
1
2
(
x
)
+
c
2
2
ϕ
2
2
(
x
)
+
c
3
2
ϕ
3
2
(
x
)
I(x) = c_0^2 \phi_0^2(x) + c_1^2 \phi_1^2(x) + c_2^2 \phi_2^2(x) + c_3^2 \phi_3^2(x)
I(x)=c02ϕ02(x)+c12ϕ12(x)+c22ϕ22(x)+c32ϕ32(x)
更形象的一个表示是

系数就是原始图像的4个像素值。
Step 1:
就
V
1
V^1
V1 和
W
1
W^1
W1 的基函数的形式,
I
(
x
)
I(x)
I(x) 可以是表示为
I
(
x
)
=
c
0
1
ϕ
0
1
(
x
)
+
c
1
1
ϕ
1
1
(
x
)
+
d
0
1
ψ
0
1
(
x
)
+
d
1
1
ψ
1
1
(
x
)
I(x)= c_0^1 \phi_0^1(x) + c_1^1 \phi_1^1(x) + d_0^1 \psi_0^1(x) + d_1^1\psi_1^1(x)
I(x)=c01ϕ01(x)+c11ϕ11(x)+d01ψ01(x)+d11ψ11(x)

Step 2:
就
V
0
V^0
V0 和
W
0
W^0
W0 的基函数的形式,
I
(
x
)
I(x)
I(x) 可以是表示为
I
(
x
)
=
c
0
0
ϕ
0
0
(
x
)
+
d
0
0
ψ
0
0
(
x
)
+
d
0
1
ψ
0
1
(
x
)
+
d
1
1
ψ
1
1
(
x
)
I(x)= c_0^0 \phi_0^0(x) + d_0^0 \psi_0^0(x) + d_0^1 \psi_0^1(x) + d_1^1\psi_1^1(x)
I(x)=c00ϕ00(x)+d00ψ00(x)+d01ψ01(x)+d11ψ11(x)

4. 正交性
Haar 基具有一个非常重要的性质就是正交性。
5. 标准化
如果 一个基函数 f ( x ) f(x) f(x) 满足 < f , f > = 1 <f,f> = 1 <f,f>=1则称它们是标准基。
参考资料
[1] Wavelets for computer Graphics: A Primer, Part 1























 930
930

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








