在生活中,我们把描述事物之间的关系称之为函数。它有两种情况:一类是用离散数据表示的;另一类是有明显的表达式,但是表达式普遍很复杂,不易于计算和使用。为了解决这个问题,我们可以在一定的误差范围内,用一个简单易算的近似表达式来替代真实的函数。(这种思想和我们大脑的替代思维是一样的,可以阅读《思考,快与慢》)
用简单的函数来近似真实函数,最常用的简单函数就是多项式 P ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + a n x n P(x) = a_0+a_1x + a_2x^2 + \cdots + a_nx^n P(x)=a0+a1x+a2x2+⋯+anxn 。因为它只用到加减乘运算,而且它的导数、积分也比较容易计算。这种用多项式来近似真实的表格函数或者复杂函数的方法称之为插值法。
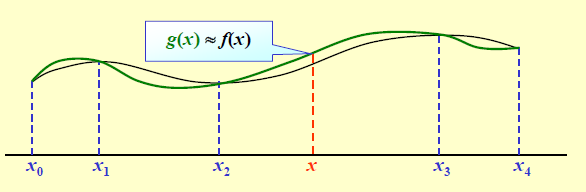
当精确函数 f ( x ) f(x) f(x) 很复杂或者未知的情况下,在一系列点 x 0 , x 1 , ⋯ , x n x_0,x_1,\cdots,x_n x0,x1,⋯,xn 处测得准确值(理想状态,实际操作是不可能的) y 0 = f ( x 0 ) , y 1 = f ( x 1 ) , ⋯ , y n = f ( x n ) y_0=f(x_0),y_1=f(x_1),\cdots,y_n=f(x_n) y0=f(x0),y1=f(x1),⋯,yn=f(xn) ,我们据此可以构造一个简单易算的近似函数 g ( x ) ≈ f ( x ) g(x) \approx f(x) g(x)≈f(x) ,满足条件: y i = g ( x i ) ( i = 0 , 1 , ⋯ , n ) y_i = g(x_i)(i=0,1,\cdots,n) yi=g(xi)(i=0,1,⋯,n) ,这时 g ( x ) g(x) g(x) 称为 f ( x ) f(x) f(x) 的插值函数。
1. Lagrange 插值
预备知识
线性插值
插值的灵感来源于线性插值,即 P 1 ( x ) = a 0 + a 1 x P_1(x) = a_0 + a_1 x P1(x)=a0+a1x 。已知两个节点 ( x 0 , y 0 ) , ( x 1 , y 1 ) (x_0,y_0),(x_1,y_1) (x0,y0),(x1,y1) ,求 P 1 ( x ) P_1(x) P1(x) 使得 P 1 ( x 0 ) = y 0 , P 1 ( x 1 ) = y 1 P_1(x_0)=y_0,P_1(x_1)=y_1 P1(x0)=y0,P1(x1)=y1 。
这难道不就是我们初中时学的两点确定直线的公式吗?它有两种方法:一种是两点式
P
1
(
x
)
=
x
−
x
1
x
0
−
x
1
y
0
+
x
−
x
0
x
1
−
x
0
y
1
\begin{aligned} P_1(x) = \frac{x-x_1}{x_0-x_1}y_0 + \frac{x-x_0}{x_1-x_0}y_1 \end{aligned}
P1(x)=x0−x1x−x1y0+x1−x0x−x0y1
上式是Lagrange插值的思想来源。另一种是点斜式
P
1
(
x
)
=
y
0
+
y
1
−
y
0
x
1
−
x
0
(
x
−
x
0
)
\begin{aligned} P_1(x) = y_0 + \frac{y_1 - y_0}{x_1 - x_0}(x - x_0) \end{aligned}
P1(x)=y0+x1−x0y1−y0(x−x0)
这种方法是牛顿插值的思想来源。
二次插值
那么已知三个节点 ( x 0 , y 0 ) , ( x 1 , y 1 ) , ( x 2 , y 2 ) (x_0,y_0),(x_1,y_1),(x_2,y_2) (x0,y0),(x1,y1),(x2,y2) 如何构造一个二次插值 P 2 ( x ) = a 0 + a 1 x + a 2 x 2 P_2(x) = a_0+a_1x+a_2x^2 P2(x)=a0+a1x+a2x2 且满足 P 2 ( x 0 ) = y 0 , P 2 ( x 1 ) = y 1 , P 2 ( x 2 ) = y 2 P_2(x_0)=y_0,P_2(x_1)=y_1,P_2(x_2)=y_2 P2(x0)=y0,P2(x1)=y1,P2(x2)=y2 呢?
想必大家也想到了待定系数法,我们何不把每一个已知点代入
P
2
(
x
)
P_2(x)
P2(x) 呢?
{
y
0
=
a
0
+
a
1
x
0
+
a
2
x
0
2
y
1
=
a
0
+
a
1
x
1
+
a
2
x
1
2
y
2
=
a
0
+
a
1
x
2
+
a
2
x
2
2
⇒
[
y
0
y
1
y
2
]
=
[
1
x
0
x
0
2
1
x
1
x
1
2
1
x
2
x
2
2
]
[
a
0
a
1
a
2
]
\left\{ \begin{aligned} y_0 &= a_0 + a_1x_0 + a_2x_0^2 \\ y_1 &= a_0 + a_1x_1 + a_2x_1^2 \\ y_2 &= a_0 + a_1x_2 + a_2x_2^2 \end{aligned} \right. \Rightarrow \begin{bmatrix} y_0 \\ y_1 \\ y_2 \end{bmatrix}= \begin{bmatrix} 1 & x_0 & x_0^2 \\ 1 & x_1 & x_1^2 \\ 1 & x_2 & x_2^2 \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \end{bmatrix}
⎩⎪⎨⎪⎧y0y1y2=a0+a1x0+a2x02=a0+a1x1+a2x12=a0+a1x2+a2x22⇒⎣⎡y0y1y2⎦⎤=⎣⎡111x0x1x2x02x12x22⎦⎤⎣⎡a0a1a2⎦⎤
当
x
0
,
x
1
,
x
2
x_0,x_1,x_2
x0,x1,x2 互异时,系数矩阵非奇异,以上方程组存在惟一解,但是线性方程组的求解是不容易的。我们能否再找到一种简单的方法呢?我们是否可以从线性插值的两种表达式中找到规律,进行归纳呢?
Lagrange 插值
这种插值是基于对线性插值中的两点式进行思考归纳的。
P
1
(
x
)
=
x
−
x
1
x
0
−
x
1
y
0
+
x
−
x
0
x
1
−
x
0
y
1
=
∑
i
=
0
1
l
i
(
x
)
y
i
\begin{aligned} P_1(x) = \frac{x-x_1}{x_0-x_1}y_0 + \frac{x-x_0}{x_1-x_0}y_1 = \displaystyle \sum_{i=0}^1 l_i(x)y_i \end{aligned}
P1(x)=x0−x1x−x1y0+x1−x0x−x0y1=i=0∑1li(x)yi
从上式中定义的
l
i
(
x
)
l_i(x)
li(x) 可以发现:
l
i
(
x
i
)
=
1
,
l
i
(
x
j
)
=
0
(
j
≠
i
)
l_i(x_i) = 1,l_i(x_j) = 0(j \neq i)
li(xi)=1,li(xj)=0(j=i) ,即
l
i
(
x
)
=
δ
i
j
l_i(x) = \delta_{ij}
li(x)=δij 。因此称之为线性插值的基函数。受这种启发,我们是不是可以假设二次插值也可以有这种形式呢?即
P
2
(
x
)
=
l
0
(
x
)
y
0
+
l
1
(
x
)
y
1
+
l
2
(
x
)
y
2
\begin{aligned} P_2(x) = l_0(x)y_0 + l_1(x)y_1 + l_2(x)y_2 \end{aligned}
P2(x)=l0(x)y0+l1(x)y1+l2(x)y2
其中,
l
0
(
x
)
,
l
1
(
x
)
,
l
2
(
x
)
l_0(x),l_1(x),l_2(x)
l0(x),l1(x),l2(x) 都是二次多项式,且满足
| x 0 x_0 x0 | x 1 x_1 x1 | x 2 x_2 x2 | |
|---|---|---|---|
| l 0 ( x ) l_0(x) l0(x) | 1 | 0 | 0 |
| l 1 ( x ) l_1(x) l1(x) | 0 | 1 | 0 |
| l 2 ( x ) l_2(x) l2(x) | 0 | 0 | 1 |
通过零点,我们可以假设
l
0
(
x
)
=
λ
(
x
−
x
1
)
(
x
−
x
2
)
l_0(x) = \lambda(x-x_1)(x-x_2)
l0(x)=λ(x−x1)(x−x2) ,又因为
l
1
(
x
0
)
=
1
l_1(x_0) = 1
l1(x0)=1 可得
λ
=
1
(
x
0
−
x
1
)
(
x
0
−
x
2
)
\lambda = \frac{1}{(x_0-x_1)(x_0-x_2)}
λ=(x0−x1)(x0−x2)1 从而
l
0
(
x
)
=
(
x
−
x
1
)
(
x
−
x
2
)
(
x
0
−
x
1
)
(
x
0
−
x
2
)
\begin{aligned} l_0(x) = \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} \end{aligned}
l0(x)=(x0−x1)(x0−x2)(x−x1)(x−x2)
同理可得
l
1
(
x
)
,
l
2
(
x
)
l_1(x),l_2(x)
l1(x),l2(x) 。因此三个节点的二次插值公式为
P
2
(
x
)
=
(
x
−
x
1
)
(
x
−
x
2
)
(
x
0
−
x
1
)
(
x
0
−
x
2
)
y
0
+
(
x
−
x
0
)
(
x
−
x
2
)
(
x
1
−
x
0
)
(
x
1
−
x
2
)
y
1
+
(
x
−
x
0
)
(
x
−
x
1
)
(
x
2
−
x
0
)
(
x
0
−
x
1
)
y
2
\begin{aligned} P_2(x) = \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}y_0 + \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}y_1 + \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_0-x_1)}y_2 \end{aligned}
P2(x)=(x0−x1)(x0−x2)(x−x1)(x−x2)y0+(x1−x0)(x1−x2)(x−x0)(x−x2)y1+(x2−x0)(x0−x1)(x−x0)(x−x1)y2
n次插值
已知 ( x 0 , y 0 ) , ( x 1 , y 1 ) , ⋯ , ( x n , y n ) (x_0,y_0),(x_1,y_1),\cdots,(x_n,y_n) (x0,y0),(x1,y1),⋯,(xn,yn) 共 n + 1 n+1 n+1 个节点,如何构造一个多项式 P n ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + a n x n P_n(x) = a_0 +a_1 x + a_2x^2 + \cdots + a_nx^n Pn(x)=a0+a1x+a2x2+⋯+anxn 去拟合真实的函数 f ( x ) f(x) f(x) ?并使得 P n ( x i ) = y i , ( i = 0 , 1 , ⋯ , n ) P_n(x_i) = y_i,(i=0,1,\cdots,n) Pn(xi)=yi,(i=0,1,⋯,n) 。
受二次插值的启发,我们可以假设
P
n
(
x
)
=
∑
i
=
0
n
l
i
(
x
)
y
i
P_n(x) = \displaystyle \sum_{i=0}^n l_i(x)y_i
Pn(x)=i=0∑nli(x)yi
其中,
l
i
(
x
)
l_i(x)
li(x) 是
n
n
n 次多项式且
l
i
(
x
j
)
=
δ
i
j
l_i(x_j)=\delta_{ij}
li(xj)=δij 。显然,这种假设下,
P
n
(
x
)
P_n(x)
Pn(x) 满足
P
n
(
x
i
)
=
y
i
,
(
i
=
0
,
1
,
⋯
,
n
)
P_n(x_i) = y_i,(i=0,1,\cdots,n)
Pn(xi)=yi,(i=0,1,⋯,n) ,接下来就可以通过它的性质进行求解具体的
l
i
(
x
)
l_i(x)
li(x) 。
因为
l
i
(
x
)
l_i(x)
li(x) 是
n
n
n 次的,且它的零点是
x
0
,
x
1
,
⋯
,
x
i
−
1
,
x
i
+
1
,
⋯
,
x
n
x_0,x_1,\cdots,x_{i-1},x_{i+1},\cdots,x_n
x0,x1,⋯,xi−1,xi+1,⋯,xn ,因此可以假设
l
i
(
x
)
=
λ
i
(
x
−
x
0
)
(
x
−
x
1
)
⋯
(
x
−
x
i
−
1
)
(
x
−
x
i
+
1
)
⋯
(
x
−
x
n
)
=
λ
i
∏
j
=
0
,
j
≠
i
n
(
x
−
x
j
)
\begin{aligned} l_i(x) &= \lambda_i (x-x_0)(x-x_1)\cdots(x-x_{i-1})(x-x_{i+1})\cdots(x-x_n) &= \lambda_i \displaystyle \prod_{j=0,j \neq i}^n (x-x_j) \end{aligned}
li(x)=λi(x−x0)(x−x1)⋯(x−xi−1)(x−xi+1)⋯(x−xn)=λij=0,j=i∏n(x−xj)
又因为
l
i
(
x
i
)
=
1
l_i(x_i) = 1
li(xi)=1 可知
λ
i
=
∏
j
=
0
,
j
≠
i
n
1
x
i
−
x
j
\begin{aligned} \lambda_i = \displaystyle \prod_{j=0,j\neq i}^n \frac{1}{x_i-x_j} \end{aligned}
λi=j=0,j=i∏nxi−xj1
因此,可以得到
l
i
(
x
)
=
∏
j
=
0
,
j
≠
i
n
x
−
x
j
x
i
−
x
j
\begin{aligned} l_i(x) = \displaystyle \prod_{j=0,j\neq i}^n \frac{x-x_j}{x_i-x_j} \end{aligned}
li(x)=j=0,j=i∏nxi−xjx−xj
经过计算,我们可以得到一个
L
n
(
x
)
=
∑
i
=
0
n
l
i
(
x
)
y
i
L_n(x)=\displaystyle \sum_{i=0}^n l_i(x)y_i
Ln(x)=i=0∑nli(x)yi ,可以发现这个所构造的多项式函数只与节点有关,与其真实函数
f
(
x
)
f(x)
f(x) 无关。
在假设条件下所得出的多项式,是唯一存在的吗?会不会和待定系数法求出的多项式的系数不一样啊?不用担心,这里有一条定理保证:
定 理 : 满 足 P ( x i ) = y i , i = 0 , 1 , ⋯ , n 的 n 阶 插 值 多 项 式 是 惟 一 存 在 的 . 定理:满足P(x_i)=y_i,i=0,1,\cdots,n 的n阶插值多项式是惟一存在的. 定理:满足P(xi)=yi,i=0,1,⋯,n的n阶插值多项式是惟一存在的.
插值余项
既然 P n ( x ) ≈ f ( x ) P_n(x) \approx f(x) Pn(x)≈f(x) ,那么这个插值函数与真实函数究竟有多相似呢?我们需要对误差进行衡量和控制,令 R n ( x ) = f ( x ) − P n ( x ) R_n(x) = f(x) - P_n(x) Rn(x)=f(x)−Pn(x) ,称之为插值余项。
R
n
(
x
)
R_n(x)
Rn(x) 至少有
n
+
1
n+1
n+1 个根,分别为
x
0
,
x
1
,
⋯
,
x
n
x_0,x_1,\cdots,x_n
x0,x1,⋯,xn ,因此有
R
n
(
x
)
=
K
(
x
)
∏
i
=
0
n
(
x
−
x
i
)
R_n(x) = K(x)\displaystyle\prod_{i=0}^n (x-x_i)
Rn(x)=K(x)i=0∏n(x−xi) ,其中
K
(
x
)
K(x)
K(x) 是一个关于
x
x
x 的待定函数。现在固定
x
≠
x
i
(
i
=
0
,
1
,
⋯
,
n
)
x \neq x_i (i=0,1,\cdots,n)
x=xi(i=0,1,⋯,n) ,构造以下函数
ψ
(
t
)
=
R
n
(
t
)
−
K
(
x
)
∏
i
=
0
n
(
t
−
x
i
)
\begin{aligned} \psi(t) = R_n(t) - K(x)\displaystyle\prod_{i=0}^n (t-x_i) \end{aligned}
ψ(t)=Rn(t)−K(x)i=0∏n(t−xi)
ψ
(
t
)
\psi(t)
ψ(t) 显然至少具有
n
+
2
n+2
n+2 个根
x
0
,
x
1
,
⋯
,
x
n
,
x
x_0,x_1,\cdots,x_n,x
x0,x1,⋯,xn,x 。根据罗尔定理,如果此时的
ψ
(
t
)
\psi(t)
ψ(t) 足够的光滑,那么就在区间上存在一个
ζ
\zeta
ζ ,使得
ψ
n
+
1
(
ζ
)
=
0
\psi^{n+1}(\zeta) = 0
ψn+1(ζ)=0 从而有以下推导:
f
n
+
1
(
ζ
)
−
P
n
n
+
1
(
ζ
)
−
K
(
x
)
(
n
+
1
)
!
=
0
f
n
+
1
(
ζ
)
=
K
(
x
)
(
n
+
1
)
!
K
(
x
)
=
f
n
+
1
(
ζ
)
(
n
+
1
)
!
\begin{aligned} f^{n+1}(\zeta) - P_n^{n+1}(\zeta) -K(x)(n+1)! &= 0 \\ f^{n+1}(\zeta) &= K(x)(n+1)! \\ K(x) & = \frac{f^{n+1}(\zeta)}{(n+1)!} \end{aligned}
fn+1(ζ)−Pnn+1(ζ)−K(x)(n+1)!fn+1(ζ)K(x)=0=K(x)(n+1)!=(n+1)!fn+1(ζ)
故 $R_n(x) = \frac{f^{n+1}(\zeta)}{(n+1)!} \displaystyle\prod_{i=0}^n (x-x_i) $ ,称为之插值余项。最后,再来说一下
ψ
(
t
)
\psi(t)
ψ(t) 足够光滑的条件,其实只需要
f
∈
C
n
[
a
,
b
]
f\in C^n[a,b]
f∈Cn[a,b] 且
f
n
+
1
f^{n+1}
fn+1 在区间上存在即可。
插值余项公式中的 ζ \zeta ζ 并不容易找到,因此一般来说我们只考虑 ∣ f n + 1 ∣ < M n + 1 , ∀ x ∈ [ a , b ] |f^{n+1}| < M_{n+1}, \forall x \in [a,b] ∣fn+1∣<Mn+1,∀x∈[a,b] ,将 M n + 1 ( ζ ) ( n + 1 ) ! ∏ i = 0 n ( x − x i ) \frac{M_{n+1}(\zeta)}{(n+1)!} \displaystyle\prod_{i=0}^n (x-x_i) (n+1)!Mn+1(ζ)i=0∏n(x−xi) 作为误差估计上限。
同时可以看出,插值多项式对于一个次数 ≤ n \le n ≤n 的多项式是精确的,因为此时的 f n + 1 ( x ) = 0 , K ( x ) = 0 , R n ( x ) = 0 f^{n+1}(x) = 0,K(x) = 0,R_n(x)=0 fn+1(x)=0,K(x)=0,Rn(x)=0 。
客观评价
优点:Lagrange插值法结构简单,基函数容易构造,在理论分析上简单明了,计算机编程容易。
缺点:计算量大,每一个基函数都是一个 n n n 阶的多项式,一共 n + 1 n+1 n+1 项;最大的卡脖子点就是当节点数目增加时,所有的基函数都需要重新计算,造成之前工作的浪费,即没有“承袭性”。
针对“承袭性”问题,提出了新的插值方法——牛顿法。
2. 牛顿插值
牛顿插值的灵感来源于两点之间的点斜式公式。
P
1
(
x
)
=
y
0
+
y
1
−
y
0
x
1
−
x
0
(
x
−
x
0
)
=
f
(
x
0
)
+
f
(
x
1
)
−
f
(
x
0
)
x
1
−
x
0
(
x
−
x
0
)
=
f
(
x
0
)
+
f
[
x
0
,
x
1
]
(
x
−
x
0
)
\begin{aligned} P_1(x) &= y_0 + \frac{y_1-y_0}{x_1-x_0}(x-x_0) \\ &= f(x_0) + \frac{f(x_1)-f(x_0)}{x_1-x_0}(x-x_0) \\ &= f(x_0) + f[x_0,x_1](x-x_0) \end{aligned}
P1(x)=y0+x1−x0y1−y0(x−x0)=f(x0)+x1−x0f(x1)−f(x0)(x−x0)=f(x0)+f[x0,x1](x−x0)
可以发现,
P
1
(
x
)
P_1(x)
P1(x) 中的
f
(
x
1
)
−
f
(
x
0
)
x
1
−
x
0
\frac{f(x_1)-f(x_0)}{x_1-x_0}
x1−x0f(x1)−f(x0) 是一个常数,它只与
x
0
,
x
1
x_0,x_1
x0,x1 两个节点有关,因此可以这样表示
f
[
x
0
,
x
1
]
f[x_0,x_1]
f[x0,x1]。
定
义
:
称
f
[
x
0
,
x
k
]
=
f
(
x
k
)
−
f
(
x
0
)
x
k
−
x
0
为
f
(
x
)
关
于
点
x
0
,
x
k
的
一
阶
均
差
;
f
[
x
0
,
x
1
,
x
k
]
=
f
[
x
0
,
x
k
]
−
f
[
x
0
,
x
1
]
x
k
−
x
1
为
f
(
x
)
的
二
阶
均
差
;
一
般
的
,
称
f
[
x
0
,
x
1
,
⋯
,
x
k
]
=
f
[
x
0
,
x
1
,
⋯
,
x
k
−
2
,
x
k
]
−
f
[
x
0
,
x
1
,
⋯
,
x
k
−
2
,
x
k
−
1
]
x
k
−
x
k
−
1
为
f
(
x
)
的
k
阶
均
差
。
定义:称f[x_0,x_k] = \frac{f(x_k)-f(x_0)}{x_k-x_0}为f(x)关于点x_0,x_k的一阶均差;\\f[x_0,x_1,x_k] = \frac{f[x_0,x_k] - f[x_0,x_1]}{x_k-x_1}为f(x)的二阶均差;\\一般的,称f[x_0,x_1,\cdots,x_k] = \frac{f[x_0,x_1,\cdots,x_{k-2},x_k]-f[x_0,x_1,\cdots,x_{k-2},x_{k-1}]}{x_{k}-x_{k-1}}为f(x)的k阶均差。
定义:称f[x0,xk]=xk−x0f(xk)−f(x0)为f(x)关于点x0,xk的一阶均差;f[x0,x1,xk]=xk−x1f[x0,xk]−f[x0,x1]为f(x)的二阶均差;一般的,称f[x0,x1,⋯,xk]=xk−xk−1f[x0,x1,⋯,xk−2,xk]−f[x0,x1,⋯,xk−2,xk−1]为f(x)的k阶均差。
受此启发,我们也希望二次插值也能有这种有规律的结构,因此假设
P
2
(
x
)
=
α
0
+
α
1
(
x
−
x
0
)
+
α
2
(
x
−
x
0
)
(
x
−
x
1
)
\begin{aligned} P_2(x) = \alpha_0 + \alpha_1(x-x_0) + \alpha_2(x-x_0)(x-x_1) \end{aligned}
P2(x)=α0+α1(x−x0)+α2(x−x0)(x−x1)
通过待定系数法,由
P
2
(
x
0
)
=
y
0
P_2(x_0) = y_0
P2(x0)=y0 得
α
0
=
f
(
x
0
)
\alpha_0= f(x_0)
α0=f(x0);由
P
2
(
x
1
)
=
y
1
P_2(x_1) = y_1
P2(x1)=y1 得 $\alpha_1= \frac{f(x_1)-f(x_0)}{x_1-x_0} = f[x_0,x_1] $;由
P
2
(
x
2
)
=
y
2
P_2(x_2) = y_2
P2(x2)=y2 得 $\alpha_2 = \frac{f[x_0,x_2] - f[x_0,x_1]}{x_2-x_1} = f[x_0,x_1,x_2] $ 。
结果发现,此时的 P 2 ( x ) P_2(x) P2(x) 可以看作是一组特殊函数 1 , ( x − x 0 ) , ( x − x 0 ) ( x − x 1 ) 1,(x-x_0),(x-x_0)(x-x_1) 1,(x−x0),(x−x0)(x−x1) 的线性组合,由此可以说这种方法也是一种基函数法。
对于
n
+
1
n+1
n+1 个节点的插值公式
P
n
(
x
)
P_n(x)
Pn(x) , 我们也希望是上述一组特殊函数
1
,
(
x
−
x
0
)
,
(
x
−
x
0
)
(
x
−
x
1
)
,
⋯
,
(
x
−
x
0
)
(
x
−
x
1
)
⋯
(
x
−
x
n
)
\begin{aligned} 1,(x-x_0),(x-x_0)(x-x_1),\cdots,(x-x_0)(x-x_1)\cdots(x-x_n) \end{aligned}
1,(x−x0),(x−x0)(x−x1),⋯,(x−x0)(x−x1)⋯(x−xn)
的线性组合。不妨假设
P
n
(
x
)
=
α
0
+
α
1
(
x
−
x
0
)
+
α
2
(
x
−
x
0
)
(
x
−
x
1
)
+
⋯
+
α
n
(
x
−
x
0
)
(
x
−
x
1
)
⋯
(
x
−
x
n
−
1
)
\begin{aligned} P_n(x) = \alpha_0 + \alpha_1(x-x_0) + \alpha_2(x-x_0)(x-x_1) + \cdots + \alpha_n(x-x_0)(x-x_1)\cdots(x-x_{n-1}) \end{aligned}
Pn(x)=α0+α1(x−x0)+α2(x−x0)(x−x1)+⋯+αn(x−x0)(x−x1)⋯(x−xn−1)
那么上式的组合系数是多少呢?同样我们可以通过待定系数法来确定,并且发现它们之间是有规律的。
α
0
=
f
(
x
0
)
α
1
=
f
(
x
1
)
−
f
(
x
0
)
x
1
−
x
0
=
f
[
x
0
,
x
1
]
α
2
=
f
(
x
2
)
−
f
(
x
0
)
x
2
−
x
0
−
f
(
x
1
)
−
f
(
x
0
)
x
1
−
x
0
x
2
−
x
1
=
f
[
x
0
,
x
1
,
x
2
]
⋮
\begin{aligned} \alpha_0 & = f(x_0) \\ \alpha_1 & = \frac{f(x_1)-f(x_0)}{x_1-x_0} = f[x_0,x_1]\\ \alpha_2 & = \frac{\frac{f(x_2)-f(x_0)}{x_2-x_0} -\frac{f(x_1)-f(x_0)}{x_1-x_0}}{x_2 -x_1} = f[x_0,x_1,x_2] \\ \vdots \end{aligned}
α0α1α2⋮=f(x0)=x1−x0f(x1)−f(x0)=f[x0,x1]=x2−x1x2−x0f(x2)−f(x0)−x1−x0f(x1)−f(x0)=f[x0,x1,x2]
依次递推可以得到
α
k
\alpha_k
αk 的表达式。
牛顿插值公式
f ( x ) = f ( x 0 ) + ( x − x 0 ) f [ x , x 0 ] f [ x , x 0 ] = f [ x 0 , x 1 ] + ( x − x 1 ) f [ x , x 0 , x 1 ] f [ x , x 0 , x 1 ] = f [ x 0 , x 1 , x 2 ] + ( x − x 2 ) f [ x , x 0 , x 1 , x 2 ] ⋮ f [ x , x 0 , x 1 , ⋯ , x n − 1 ] = f [ x 0 , x 1 , ⋯ , x n ] + ( x − x n ) f [ x , x 0 , x 1 , ⋯ , x n ] \begin{aligned} f(x) &= f(x_0) + (x-x_0)f[x,x_0] \\ f[x,x_0] &= f[x_0,x_1] + (x-x_1)f[x,x_0,x_1]\\ f[x,x_0,x_1] &= f[x_0,x_1,x_2] + (x-x_2)f[x,x_0,x_1,x_2]\\ & \vdots\\ f[x,x_0,x_1,\cdots,x_{n-1}] &= f[x_0,x_1,\cdots,x_n] + (x-x_n)f[x,x_0,x_1,\cdots,x_n] \end{aligned} f(x)f[x,x0]f[x,x0,x1]f[x,x0,x1,⋯,xn−1]=f(x0)+(x−x0)f[x,x0]=f[x0,x1]+(x−x1)f[x,x0,x1]=f[x0,x1,x2]+(x−x2)f[x,x0,x1,x2]⋮=f[x0,x1,⋯,xn]+(x−xn)f[x,x0,x1,⋯,xn]
通过以上公式的替换,我们可以得到
f
(
x
)
=
f
(
x
0
)
+
f
[
x
0
,
x
1
]
(
x
−
x
0
)
+
f
[
x
0
,
x
1
,
x
2
]
(
x
−
x
0
)
(
x
−
x
1
)
+
⋯
+
f
[
x
0
,
x
1
,
⋯
,
x
n
]
(
x
−
x
0
)
(
x
−
x
1
)
⋯
(
x
−
x
n
−
1
)
+
f
[
x
,
x
0
,
x
1
,
⋯
,
x
n
]
(
x
−
x
0
)
(
x
−
x
1
)
⋯
(
x
−
x
n
)
\begin{aligned} f(x) = f(x_0) + f[x_0,x_1](x-x_0) + f[x_0,x_1,x_2](x-x_0)(x-x_1)+\cdots+ f[x_0,x_1,\cdots,x_n]\\(x-x_0)(x-x_1)\cdots(x-x_{n-1}) + f[x,x_0,x_1,\cdots,x_n](x-x_0)(x-x_1)\cdots(x-x_{n}) \end{aligned}
f(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+⋯+f[x0,x1,⋯,xn](x−x0)(x−x1)⋯(x−xn−1)+f[x,x0,x1,⋯,xn](x−x0)(x−x1)⋯(x−xn)
其中牛顿公式为
N
n
(
x
)
=
f
(
x
0
)
+
f
[
x
0
,
x
1
]
(
x
−
x
0
)
+
f
[
x
0
,
x
1
,
x
2
]
(
x
−
x
0
)
(
x
−
x
1
)
+
⋯
+
f
[
x
0
,
x
1
,
⋯
,
x
n
]
(
x
−
x
0
)
(
x
−
x
1
)
⋯
(
x
−
x
n
−
1
)
N_n(x) = f(x_0) + f[x_0,x_1](x-x_0) + f[x_0,x_1,x_2](x-x_0)(x-x_1)+\cdots+ f[x_0,x_1,\cdots,x_n]\\(x-x_0)(x-x_1)\cdots(x-x_{n-1})
Nn(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+⋯+f[x0,x1,⋯,xn](x−x0)(x−x1)⋯(x−xn−1)
插值余项为 R n ( x ) = f [ x , x 0 , x 1 , ⋯ , x n ] ( x − x 0 ) ( x − x 1 ) ⋯ ( x − x n ) R_n(x) = f[x,x_0,x_1,\cdots,x_n](x-x_0)(x-x_1)\cdots(x-x_{n}) Rn(x)=f[x,x0,x1,⋯,xn](x−x0)(x−x1)⋯(x−xn)
3. Hermite 插值
前面介绍的插值方法都是针对函数值的插值,有的时候对插值函数的要求更高,不仅需要满足在特定点的函数值准确,还要求其特定点处的光滑程度也准确,即在特定点的若干阶导数值也准确,从数学角度来说就是插值函数 ψ ( x ) \psi(x) ψ(x) 需要满足: ψ ( x i ) = f ( x i ) , ψ ′ ( x i ) = f ′ ( x i ) , ⋯ , , ψ ( m ) ( x i ) = f ( m ) ( x i ) \psi(x_i)=f(x_i), \psi'(x_i) = f'(x_i),\cdots,,\psi^{(m)}(x_i)=f^{(m)}(x_i) ψ(xi)=f(xi),ψ′(xi)=f′(xi),⋯,,ψ(m)(xi)=f(m)(xi) 。
那么此时的插值函数如何构造呢?我们还是基于基函数的理念。
例题:若已知 f ( x 0 ) , f ( x 1 ) , f ( x 2 ) , f ′ ( x 0 ) ( x 0 ≠ x 1 ≠ x 2 f(x_0),f(x_1),f(x_2),f'(x_0)(x_0\neq x_1 \neq x_2 f(x0),f(x1),f(x2),f′(x0)(x0=x1=x2 的值,求多项式 P ( x ) P(x) P(x) 满足 P ( x 0 ) = f ( x 0 ) , P ( x 1 ) = f ( x 1 ) , P ( x 2 ) = f ( x 2 ) , P ′ ( x 0 ) = f ′ ( x 0 ) P(x_0) = f(x_0),P(x_1) = f(x_1),P(x_2)=f(x_2),P'(x_0) = f'(x_0) P(x0)=f(x0),P(x1)=f(x1),P(x2)=f(x2),P′(x0)=f′(x0) 。
前面也提到有 n n n 个条件已知,可以构造一个 n − 1 n-1 n−1 阶的插值多项式,因此可以确定多项式为 P 3 ( x ) P_3(x) P3(x) 。
从之前Lagrange插值的思想进行假设, P 3 ( x ) = ∑ i = 0 2 h i ( x ) f ( x i ) + h 0 ^ ( x ) f ′ ( x 0 ) P_3(x) =\displaystyle \sum_{i=0}^2 h_i(x)f(x_i) + \hat{h_0}(x) f'(x_0) P3(x)=i=0∑2hi(x)f(xi)+h0^(x)f′(x0) 为满足条件,需有 h i ( x i ) = 1 , h i ( x j ) = 0 ( j ≠ i ) , h 0 ^ ( x j ) = 0 ( j = 0 , 1 , 2 ) , h i ′ ( x 0 ) = 0 , h 0 ^ ′ ( x 0 ) = 1 h_i(x_i) = 1,h_i(x_j) =0(j \neq i),\hat{h_0}(x_j)=0(j=0,1,2),h_i'(x_0)=0,\hat{h_0}'(x_0)=1 hi(xi)=1,hi(xj)=0(j=i),h0^(xj)=0(j=0,1,2),hi′(x0)=0,h0^′(x0)=1 。接下来通过待定系数法可以求出 P 3 ( x ) P_3(x) P3(x) 。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NJZuKokU-1593041053968)(Picture/7.png)]
4. 三次样条插值
待更新~
5. 问题与疑惑
- 已知 n n n 个条件,为什么要去构造的多项式函数是 n − 1 n-1 n−1 阶的?答: n − 1 n-1 n−1 阶的多项式函数有 n n n 个参数,这时 n n n 个方程是可以求解的。
- 插值余项证明中,构造的 ψ ( x ) \psi(x) ψ(x) 为什么这么构造?
























 3860
3860











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








