2020-08-06

行星轮系转速转矩计算(引用他人)
作者：demobilize
链接：https://www.zhihu.com/question/264462816/answer/352743028
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

1、简单行星轮系转速关系：设nS、nR、nC分别为太阳轮S、齿圈R和行星架C的转速，α为齿圈与太阳轮的齿比或节圆半径比（α称为行星轮系结构参数，大于1）。如将整个轮系看作在以－nC转动，则可认为行星架C没有转动，行星轮系等效于定轴轮系，故有：（nS－nC）∕（nR－nC）＝－α 变形得：nS＋αnR－（1+α）nC＝0 此式称为行星轮系转速特征方程2、简单行星轮系转矩关系：设FC为行星架上行星轮P的回转中心点的作用力，FS、FR分别为太阳轮S和齿圈R受到的力， rS、rR分别为太阳轮S、齿圈R的节圆半径（到共同回转中心），rC为行星架上行星轮P的回转中心点到共同回转中心的半径，rP为行星轮P的节圆半径，TS、TC、TR分别为太阳轮S、行星架C、齿圈R对行星轮P的作用力点对共同回转中心的转矩。

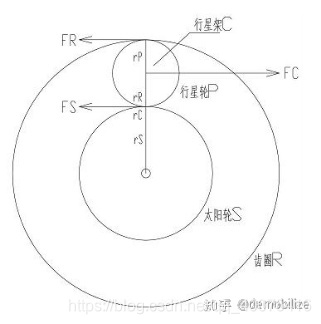
忽略轮系各转轴内摩擦力及各齿轮啮合摩擦力，根据作用力与反作用力定理及行星轮P平面力系平衡条件有：FC=－（FR+FS） （1） TC=－（TR+TS） （2）FR=FS （3） FC=－2FR=－2FS （4）即FS:FR:FC =1:1:－2 （5）由rS、rR、rC的几何关系可知：rS:rR:rC =1:α:（1+α）/2 （6）因： TS=FS×rS TR=FR×rR TC=FC×rC将（5）×（6）得：TS:TR:TC=1:α:－（1+α） 此式就是简单行星轮系太阳轮S、行星架C、齿圈R之间的转矩关系从转速特征方程和转矩关系式可看出行星轮系3个基本传动构件之间的转矩比值与转速比值互为倒数，这与普通定轴轮系传动比的性质是相同的。其原因是当忽略轮系传动各种摩擦损耗（即假设轮系传动效率为100%）时，传动轮系输入与输出功率守恒，因此转矩关系式也可通过转速特征方程和轮系传动功率守恒即TS×nS＋TR×nR ＋TC×nC＝0推出。发布于 2018-03-28