Bias-Variance Tradeoff

一、概念理解

• 偏差：将模型的期望（或平均）预测和我们正在试图预测正确值之间的差定义为偏差。
• 方差： 将模型之间的多个拟合预测之间的偏离程度定义为方差。
• 

二、数学定义

我们定义需要预测的真实结果$Y$，与其对应的自变量$X$(训练样本)，之间有这样的关系:
$Y=f(X)+ϵ$ (我们认为$ϵ$满足正态分布$ϵ\sim N(0,\sigma ϵ))’$。
令$y_D$为$x$在测试样本中的值，$y$为真实的值。

有可能出现噪音使得yD != y
为了方便讨论，这里假定E[ yD - y ] = 0

假设，$f_D(x)$为训练集$X$上学得模型$f$在$x$上的预测输出，学习算法的期望预测为：
$f_{ExpectedD}(x)=E[f_D(x)]$

统计学习中有一个重要概念叫做residual sum-of-squares：

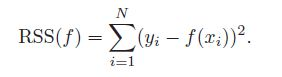
RSS看起来是一个非常合理的统计模型优化目标。但是考虑K-NN的例子，在最近邻的情况下（K=1），RSS=0，是不是KNN就是一个完美的模型了呢，显然不是，KNN有很多明显的问题，比如对训练数据量的要求很大，很容易陷入维度灾难中。

KNN的例子说明仅仅优化RSS是不充分的，因为针对特定训练集合拟合很好的model，并不能说明这个model的泛化能力好，而泛化能力恰恰又是机器学习模型的最重要的要求。真正能说明问题的不是RSS，因为它只是一个特定训练集合，而是在多个训练结合统计得出的RSS的期望，MSE（mean squared error），即期望泛化误差(均方误差)。

基于假设，我们可以得到关于测试集x的MSE（mean squared error）:
$$\begin{array}{rl}MSE(x)& =E[(f_D(x)-y_D{)}^2]\\ & =E[(f_D(x)-y_D+f_{ExpectedD}(x)-f_{ExpectedD}(x){)}^2]\\ & =E[(f_D(x)-f_{ExpectedD}(x){)}^2+(f_{ExpectedD}(x)-y_D{)}^2+\\ & 2\ast (f_D(x)-f_{ExpectedD}(x))\ast (f_{ExpectedD}(x)-y_D)]\\ & =E[(f_D(x)-f_{ExpectedD}(x){)}^2]+E[(f_{ExpectedD}(x)-y_D{)}^2]+0\\ & =E[(f_D(x)-f_{ExpectedD}(x){)}^2]+E[(f_{ExpectedD}(x)-y_D-y+y{)}^2]\\ & =E[(f_D(x)-f_{ExpectedD}(x){)}^2]+E[(f_{ExpectedD}(x)-y{)}^2]\\ & +E[(y-y_D{)}^2]+2\ast E[(f_{ExpectedD}(x)-y)\ast (y-y_D)]\\ & =E[(f_D(x)-f_{ExpectedD}(x){)}^2]+E[(f_{ExpectedD}(x)-y{)}^2]\\ & +E[(y-y_D{)}^2]\\ & =va{r}^2(x)+bia{s}^2(x)+{ϵ}^2\end{array}$$
即MSE可以分解为方差，偏差与噪音之和。