图论（十三）——平面图和对偶图

一、平面图概念

\quad 如果能把图G画在平面上，使得除顶点外，边与边之间没有交叉，称G可以嵌入平面，或称G是可平面图。可平面图G的边不交叉的一种画法，称为G的一种平面嵌入，G的平面嵌入表示的图称为平面图。例如下图所示：

二、平面图的性质

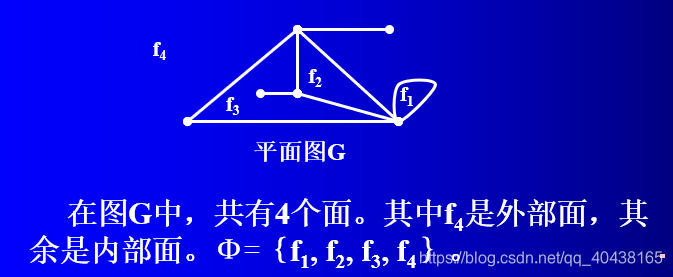
\quad 一个平面图G把平面分成若干连通片，这些连通片称为G的区域，或G的一个面。G的面组成的集合用Φ表示。

\quad 在G中，顶点和边都与某个给定区域关联的子图，称为该面的边界。某面 f 的边界中含有的边数(割边计算2次)称为该面 f 的次数, 记为deg(f)。如下图所示：

定理一：平面图的次数公式$$\sum _{f\in \Phi }deg(f)=2m$$ \quad 证明：对G的任意一条边e, 如果e是某面割边，那么由面的次数定义，该边给G的总次数贡献2次；如果e不是割边，那么，它必然是两个面的公共边，因此，由面的次数定义，它也给总次数贡献2次。

定理二：平面图的欧拉公式
设$G=(n,m)$是连通平面图，Φ是G的面数，则：$$n-m+\Phi =2$$
\quad 证明：情形1，G是树，则m=n-1,Φ=1,显然成立；情形2，G不是树的连通平面图，则G存在非割边e，显然，G-e是连通平面图，且边数为m-1，面数为Φ-1，由最小性假设，G-e满足欧拉等式：$n-(m-1)+(\Phi -1)=2$，即$n-m+\Phi =2$，得证。

欧拉公式的几个推论
1、设G是具有ф个面k个连通分支的平面图，则：$$n-m+\Phi =k+1$$证明：对第i (1≦i≦k)个分支来说，设顶点数为$n_i$，边数为$m_i$，面数为фi,由欧拉公式：$n_i-m_i+{\Phi }_i=2$，得${\sum }_{i=1}^k(n_i-m_i+{\Phi }_i)=2k$。其中，${\sum }_{i=1}^k{n}_i=n,{\sum }_{i=1}^k{m}_i=m,{\sum }_{i=1}^k{\Phi }_i=\Phi +k-1$，因此$n-m+\Phi =k+1$。

2、设G是具有n个点m条边ф个面的连通平面图，如果对G的每个面f ,有：deg(f) ≥ l ≥3,则：$$m\le \frac{l}{l-2}(n-2)$$证明：${\sum }_{f\in \Phi }deg(f)=2m\ge l\Phi ,\Phi =2-n+m\le \frac{2m}{l}$，因此$m\le \frac{l}{l-2}(n-2)$。
推论2也可叙述为若图G中$m>\frac{l}{l-2}(n-2)$,则G是非可平面图。例如，$K_{3,3}$是非可平面图，因为它每个面次数至少是4，即$l=4$，$9>\frac{4}{2}\ast (6-2)=8$，故不是可平面图。

3、简单平面图$G=(n,m)$满足：$$m\le 3n-6$$证明：因为G是简单图，所以每个面的次数至少为3，即l=3。于是，由推论2得：$m\le 3n-6$。例如，$K_5$不可平面，因为其m=10,n=5,不满足该不等式。

4、设G是具有n个点m条边的连通平面图，若G的每个圈均由长度是$l$的圈围成，则：$$m(l-2)=l(n-2)$$证明：$n-m+\frac{2m}{l}=2,l(n-m)+2m=2l,m(l-2)=l(n-2)$

5、设G是具有n个点m条边的简单平面图，则：$\delta \le 5$
反证：若$\delta \ge 6$，由握手定理，$6n\le \sum d(v)=2m,m>3n-6$，故与推论3矛盾。

三、极大平面图及其性质

定义：设G是简单可平面图，如果G是$K_i(1\leqq i\leqq 4)$,或者在G的任意非邻接顶点间添加一条边后，得到的图均是非可平面图，则称G是极大可平面图。极大可平面图的平面嵌入称为极大平面图。
显然的结论：设G是极大平面图，则G必然连通；若G结束大于等于3，则G无割边
需注意的点：顶点数相同的极大平面图并不唯一
定理一：极大平面图的三角形特征
\quad 设G是至少有3个顶点的平面图，则G是极大平面图，当且仅当G的每个面的次数是3且为单图。此时，每个面的边界是三角形。由此可推得，$m=3n-6,\Phi =2n-4$

四、极大外平面图及其性质

\quad 定义：若一个可平面图G存在一种平面嵌入，使得其所有顶点均在某个面的边界上，称该图为外可平面图。外可平面图的一种外平面嵌入，称为外平面图。设G是一个简单外可平面图，若在G中任意不邻接顶点间添上一条边后，G成为非外可平面图，则称G是极大外可平面图。极大外可平面图的外平面嵌入，称为极大外平面图。
定理1：G是一个连通简单外可平面图，则在G中有一个度数至多是2的顶点。
定理2：设G是一个有n (n≥3)个点，且所有点均在外部面上的极大外平面图，则G有n-2个内部面。
定理3：设G是一个有n (n≥3)个点，且所有点均在外部面上的外平面图，则G是极大外平面图，当且仅当其外部面的边界是圈，内部面是三角形。

四、平面图的对偶图

对于给定图G，得到G的对偶图$G^{\ast }$的规则如下：

• 在G的每个面$f_i$内取一个点$v_i^{\ast }$作为$G^{\ast }$的一个顶点
• 对G的一条边e，若e是两个面的公共边，则连接这两个面的顶点，且连线穿过e；若e是某个面割边，则以该面顶点作环，且让它与e相交。

对偶图的性质：

• $G^{\ast }$顶点数等于G的面数
• $G^{\ast }$边数等于G的边数
• $G^{\ast }$面数等于G的顶点数
• $d(v^{\ast })=deg(f)$
• 对于连通的平面图G，其$(G^{\ast }{)}^{\ast }=G$
• 同构的平面图可以有不同构的对偶图

定理一：平面图G的对偶图必然连通
欧拉图的对偶图是偶图

五、平面图的判定

\quad 对于3阶以上的具有m条边的单图G来说，如果G满足如下条件之一： (1)m>3n-6; (2) $K_5$（5阶完全图）是G的一个子图；(3) $K_{3,3}$（3阶完全偶图）是G的一个子图，那么，G是非可平面图。
\quad 下面给出平面图判定的充要条件，在此之前，我们先来看看图的两种操作——2度顶点扩充和2度顶点收缩。
\quad 在图G的边上插入一个2度顶点，使一条边分成两条边，称将图在2度顶点内扩充；去掉一个图的2度顶点，使关联它们的两条边合并成一条边，称将图G在2度顶点内收缩。

\quad 定义两图同胚，即通过反复在2度顶点扩充或收缩后能够变成一对同构的图。
\quad 重头戏来啦，库拉托斯基给出了平面图判定的充要条件，如下：图G是可平面的，当且仅当它不含$K_5$或$K_{3,3}$同胚的子图。
\quad 判断一张图是否是平面图，可以首先看看其子图经过2度顶点操作能不能变成五阶完全图，我们需要知道五阶完全图每个顶点的度数是4，如果不能，再看看能不能变成$k_{3,3}$，$k_{3,3}$每个顶点度数为3。
\quad 与之相似的判定定理是瓦格纳提出来的：设u，v是简单图G的一条边。去掉该边，重合其端点，在删去由此产生的环和平行边。这一过程称为图G的初等收缩或图的边收缩运算。简单图G是可平面图当且仅当它不含有可收缩到$K_5$或$K_{3,3}$的子图。
\quad 一个用枚举法证明的小定理：至少有9个顶点的简单可平面图的补图是不可平面的，而9是这个数目中的最小的一个。