三次B样条插值和误差分析

关键字：基函数，控制点，节点

参考：http://www.docin.com/p-1511846558.html 

前言：之前写写过一篇B样条曲线，这篇是原文的深度扩展，是针对B样条曲线的一种特殊情况，三次B样条，讨论了其插值和误差分析，添加了一些个人总结。

思路：根据已知的型值点（就是给出的已知的数据点），采用均匀参数法构造节点矢量，得到基函数的表达形式，然后利用逼近思想构造三对角阵，利用追赶法求控制点，最后拟合。

一、目的和思想

由已知的观测点，为物理量（未知量）建立一个简单的，连续的解析模型，根据该模型推测在非观测点的特性。

B样条相比于分段线性插值，在节点处可导，具有光滑性，这是它的优点。

构造思想在于通过给定的型值点反求出控制点，从而拟合曲线，可以通过更改控制点改变曲线形状。

实际B样条计算的两种情况：第一种就是本文的构造思想（上一行）。第二种是直接给出控制点。

二、定义

2.1 B样条

控制点为Pi(i=0,1,2,....,n)，p次B样条曲线方程为

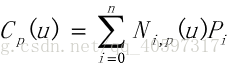
是p次B样条基函数，为节点矢量。

节点矢量的选取方法为：均匀参数法，积累弦长法，向心参数法（这里选择均匀参数法）

 

注意这里的u是一个点，可能位于的一个数，而不是像的一个向量。

为了将曲线的首末端点分别与首末数据点对应，需要将首末端点都做p+1重，即

即

注意对于p次样条，有

三、3次B样条基的计算

根据第二条性质，时，

p=3时，

其中每一项分别如下：

四、3次B样条控制点的计算

假设给定一组型值点和节点矢量，首末是四重，即，首末分别与和对应。如下图所示，那么内部节点与对应。即与对应，与对应，则r-0+1=m-3-3+1，r=m-6。所以如前文所述，这里控制节点的个数为n+1，因为m=n+p+1，所以m=n+4，那么r=n-2。

那么B样条曲线的方程为

为了求控制点Pi，采用非节点条件，将首末型值点分别对应于参数和，使得所取得的参数分别接近于，有

即

其中

化成三对角矩阵，用追赶法求解

五、B样条曲线误差分析

对于每个小区间上的点u，可以表示为

B样条曲线上一点为，注意这里的P的是二维的，第二个下标表示是第一维度的还是第二维度的。那么

继续化简，

如果分段线性插值上的点为，那么

令

那么

在每一个区间上，3次B样条曲线与折线段都会有一个或者两个功高，功高可以衡量误差的大小

令

那么

根为

B样条曲线与折线段出现一个功高，出现两个功高，曲线与折线段有交点，交点参数为曲线上点的斜率与原型点连线斜率相等时功高最大，可以用牛顿切线法找到功高最大点处，计算功高大小，判断插值好坏。