单点、双点弦截法求解方程根

弦截法：

             (a) 用牛顿法解方程f(x)=0，虽然在单根附近具有较快的收敛速度，但它有个明显的缺点，就是需要计算导数f’(x)，当f(x)比较复杂时，计算f’(x)可能有困难。

    (b)弦截法和牛顿迭代法基本思想是一样的, 也是将非线性方程f(x)=0逐步转化为线性方程求解,其区别在于牛顿法是依次用切线代替曲线,用切线的零点作为f(x)零点的近似值;弦截法用弦线代替曲线,用弦线的零点作为f(x)零点的近似值.        

                

       

所以得出：  

        

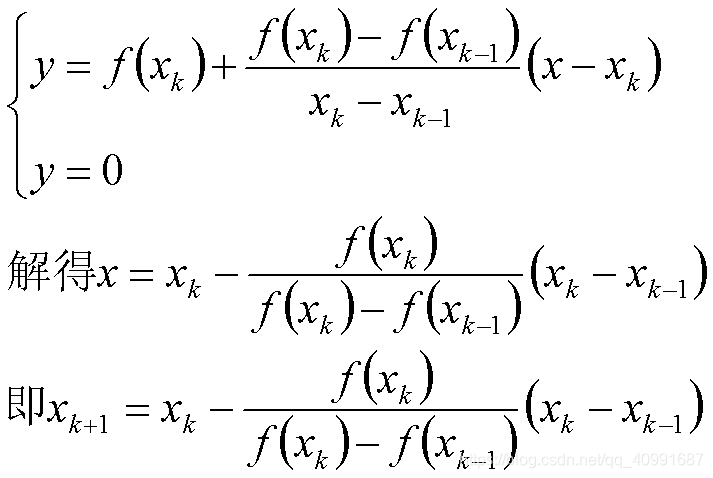
其中：

       

 

例题：使用单点、双点弦截法求方程xe^x=1在[0,1]中的根。            

#include<cstdio>
#include<cmath>
void fact(double &x0,double &x1) {//双点弦截法
	double temp=x1;
	x1=x1-(x1*exp(x1)-1)/(x1*exp(x1)-x0*exp(x0))*(x1-x0);
	x0=temp;
}
void fact1(double x0,double &x1) {//单点弦截法
	double temp=x1;
	x1=x1-(x1*exp(x1)-1)/(x1*exp(x1)-x0*exp(x0))*(x1-x0);
}
int main() {
	double x0=0,x1=1;
	while(fabs(x1-x0)>=1e-15) {
		printf("%.7lf\n",x1);
		fact(x0,x1);//双点弦截法
	}
	printf("\n");
	x0=0,x1=1;
	while(fabs(x1-x0)>=1e-15) {
		x0=x1;
		printf("%.7lf\n",x1);
		fact1(0.0,x1);//单点弦截法

	}
	return 0;
}