地震偏移处理
地震数据常规处理主要包括地震反褶积,水平叠加和地震偏移成像三大类。地震反褶积通过压缩地震子波提高地震分辨率,水平叠加的目的是提高信噪比,地震偏移成像的目的是提高地震空间分辨率和地震保真度。
在20世纪50年代,地震偏移通常是在解释好的地震剖面上根据旅行时间和同相轴的视倾角,针对每一个层位以手工方式进行的。在70年代初,演变为在二维地震构造图上或者是在 t 0 t_0 t0 时间构造图上进行手工空间校正。从70年代中期开始,对未经解释的水平地震剖面直接采用某种数学算法在计算机上进行。
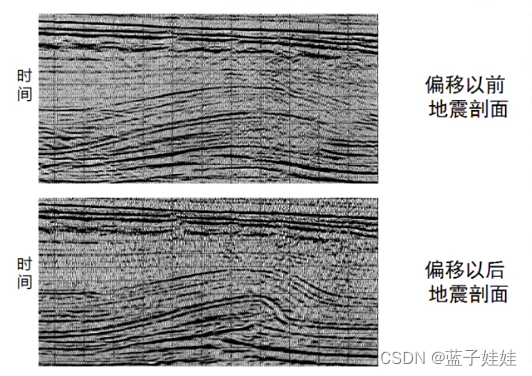
地震偏移是一个重构地震剖面的过程,可以让反射波同相轴偏移到在正确的位置空间。
在地下地层界面水平或者倾角不大的地区,水平叠加地震剖面可以较好地反映地下地质特征。但是当地下地质构造复杂,水平叠加地震剖面上,倾斜界面就会存在偏移的问题。

水平叠加地震剖面主要问题包括:倾斜界面问题,绕射波问题,向斜扭曲问题,背斜扭曲问题和断层扭曲问题等等。因此,地震偏移的主要目的就是让倾斜界面归位,绕射波回转波收敛,提高地震资料的纵横向分辨率,获得更加真实的地下图像。
在倾斜界面情况下,震源激发的地震波来自 A 点自激自收的反射波放在激发点和接收点的中点正下方B点处,其实B点已经偏移了真实的反射点A点的位置。

如下图所示,用一个圆规演示该过程。以第一个激发点为圆心,以垂直与倾斜界面的长度为半径画圆,激发点正下方的长度与自激自收法线方向射线的长度刚好相等。

对激发点2,3,4,5和6做同样的工作,这些记录点的连线就是地震剖面上倾斜界面反射波同相轴。可以看出倾斜界面反射波同相轴的位置相对真实的倾斜界面下倾,倾角小于界面倾角。
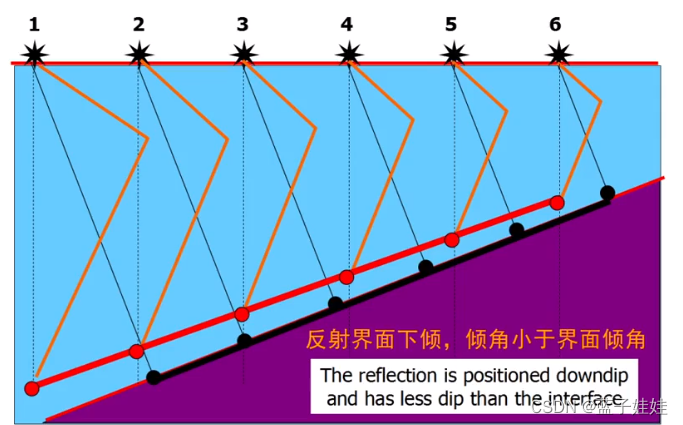
地震偏移处理就是要把倾斜界面反射波同相轴归位到正确的位置。
下图展示了实际的断面与对应的地震响应之间的偏移差异。

其实地下的一个点在水平叠加剖面上并不是一个点,根据惠更斯原理,是一条双曲线形状的绕射波,必须利用一定的偏移方法让该绕射波收敛到一个点。

在地震勘探工作中,把地震波在传播过程中遇到地层剧烈变化的地方,如断层的断点,断棱,地层尖灭点,不均匀体,侵入体和地下礁的边缘所引起的波称为绕射波。它可以看作是以这些点作为新的震源产生振动并向周围以球面波的形式传播。

假设地下有一个凹界面,比如一个向斜构造。
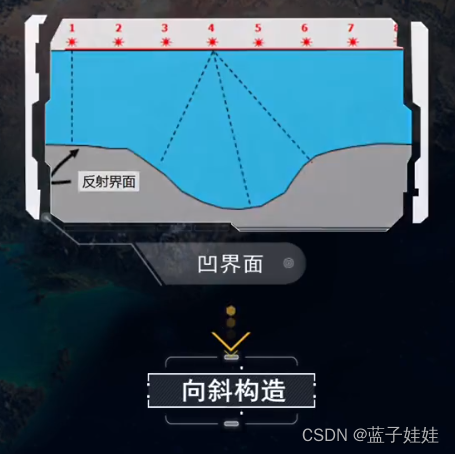
在凹界面的曲率半径小于界面深度的地方,或者当速度梯度很大时,其时距曲线会呈交叉状的反射波,叫做回转波。
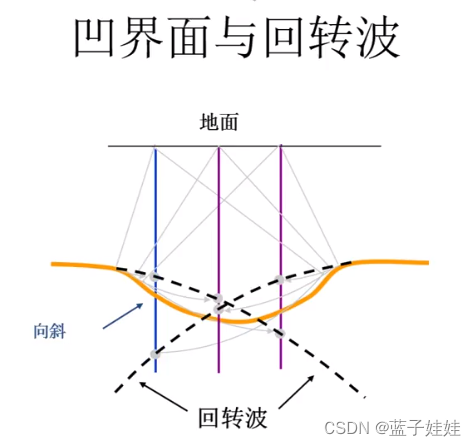
时距曲线出现交叉状的原因时凹界面两侧及平界面的反射波都到达地面上的同一点,并且时距曲线上各点的次序和它们对应的各反射点的次序是相反的。回转波的特点为视速度较小,在回转点处振幅增大,它总是和正常的反射波相伴而生,并且互相干涉。

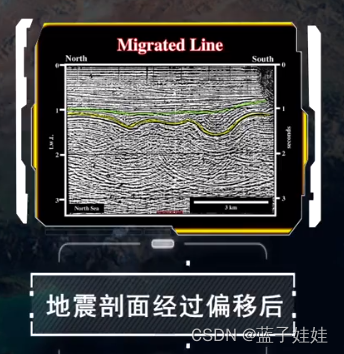
下图所示的实际的未偏移的水平叠加地震剖面的两个回转波特征十分明显…

地震剖面经偏移以后,两个回转波的地方其实是不整合面上的凹界面。
下图所示为一个凸界面的地质模型,如一个背斜构造。

凸界面为黑色的实现,在水平叠加地震剖面上被夸大为红色的虚线。
 、
、
下图展示了凸界面地质模型和对应地震剖面。在水平叠加地震剖面上被夸大了。

水平叠加剖面和地震偏移剖面关系如下:、

下图展示了一张实际的水平叠加地震剖面,不整合面上的绕射波和回转波影响了不整合的正确成像。

经过地震偏移处理后,绕射波得以收敛。回转波恢复了凹界面的真实形态。

什么时候进行地震偏移呢?倾斜反射层位置错误,断层扭曲,向斜扭曲和背斜扭曲。
地震偏移处理的主要方法
当地下地层接近水平时,水平叠加地震剖面上反映的地层形态基本符合地层情况。

但当地层倾斜时或者是起伏变化很大时,水平叠加地震剖面与实际情况就会有偏离。
为了纠正这种偏离,就需要进行地震偏移处理。

为了适应地下各种复杂的地质条件,人们将数学、物理等领域的成果应用到地震资料处理中,研究出许多地震资料处理方法,出现了许多不同的地震偏移的说法,比如二维偏移,三维偏移,叠后偏移,叠前偏移,时间偏移,深度偏移等等。
地震偏移从简单快速的方法到精确昂贵的方法各有优缺点,叠后时间偏移可以快速得到较好的地震成像;叠前时间偏移可以得到相当好的成像,但是费用较高;叠前深度偏移可以得到非常好的地震成像效果,但是费用更高。

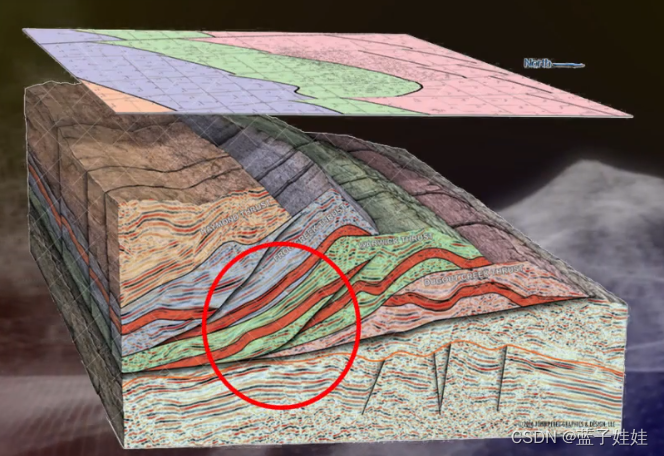
按照地震数据维数,地震偏移可以为二维地震偏移,三位地震偏移。沿着如下的三维地震模型,进行了二维和三维地震数据的采集,假设沿着粉红色的界面,进行了二维数据采集,经过处理得到水平叠加地震剖面,该剖面上绕射波和侧面波比较严重。经过二维偏移处理后,来自于侧面的黄色的侧面波仍然存在。但是经过三维地震偏移处理后,侧面波得到了归位,可以很清晰地描述地下的地质。

早期的三维偏移由于计算机速度的限制,只能进行两步法三维偏移。首先在一个方向上进行二维偏移之后,再把偏移的结构沿着另一个方向进行一次二维偏移,就得到最终的三维偏移结果。

目前可以直接使用一步法三维地震偏移。按照输入数据类型的不同,地震偏移可以分为叠后偏移和叠前偏移。叠后偏移是在水平叠加剖面上进行的,它是建立在水平层状介质,横向速度不变化的假设之上,对水平层状地层的地区,有较好的效果。叠前偏移是在共中心点道集上进行的。

对于界面倾角大,横向速度变化剧烈,叠后效果不好,需要使用叠前偏移,它直接对未叠加的数据进行处理。叠前偏移适应速度横向变化较大的地区,可以实现真正的共反射点成像,使倾斜界面正确归位。同时,利用叠前偏移的道集进行速度分析,可以获得偏移本身所需要的速度模型。
按照可以处理横向变速的不同,地震偏移可以分为时间偏移和叠前深度偏移。时间偏移假设地震波速度为常速,地震射线是直线;深度偏移的地下模型考虑到速度的横向变化,地震射线为折线,符合费马时间最短原理。

从聚焦能力看,叠前时间偏移通常比叠前深度偏移有更好的聚焦效果。从计算量看,叠前时间偏移一般比叠前深度偏移要少。
从能量归位来看,叠前深度偏移的归位更准确。从需要的速度模型看,叠前时间偏移对速度模型误差不敏感,叠前深度偏移对速度模型的误差比较敏感,因此需要的速度模型精度较高。
如下图所示的叠后零炮检距剖面上,绕射波,回转波等异常波比较严重。通过时间偏移以后的地震剖面上,不整合面以下的倾斜地层并没有得到很好的成像。通过深度偏移以后,不整合面以下的倾斜地层全部能够得到成像,比较客观地反映了地下真实的结构特征。

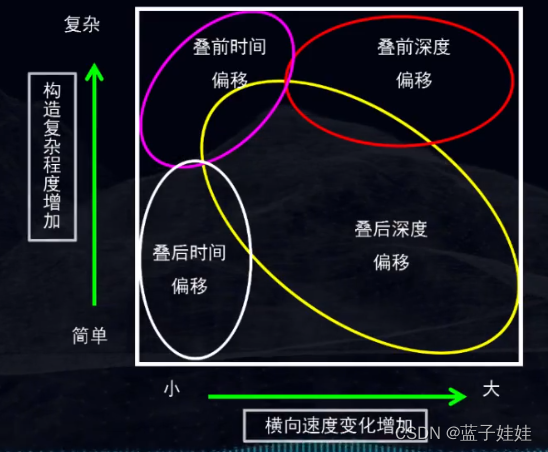
下图展示了四种偏移的关系,横轴表示速度变化,纵轴表示地下构造的复杂程度。叠后时间偏移适合地下构造变化不大,横向速度变化小的地区。叠前时间偏移适合地下构造变化较大,横向速度变化小的地区。叠后深度偏移适合地下构造变化不大,横向速度变化较大的地区。叠前深度偏移适合地下构造变化较大,横向速度变化较大的地区。
20世纪后十年发展起来的叠前深度偏移方法对复杂构造地区的地震偏移处理十分有效。如下图所示的叠后时间偏移剖面上,岩丘下的构造基本没有成像,而叠前深度偏移上岩丘下的构造特征清晰地得到了成像。

在CMP道集经过NMO校正,水平叠加之后的数据上,可以通过建立地下速度模型进行叠后深度偏移。

如果将 CMP 道集分裂为多个数据集建立速度模型进行偏移处理,然后把各个偏移处理的数据叠加起来可以得到最终的叠前深度偏移。

按照偏移速度的域的不同,地震偏移还可分为时间-空间域偏移, τ \tau τ- p p p 域地震偏移,频率-波数域偏移。
按照偏移所依赖的理论不同,地震偏移分为射线偏移和波动方程偏移。射线偏移又可分为直射线偏移和曲射线偏移。波动方程偏移又可分为声波方程偏移,弹性波方程偏移,黏弹性方程偏移,各向异性方程偏移和双相介质方程偏移。
波动方程偏移可以提高成像精度,保持地震振幅,但是需要大量的 CPU,仅支持全波场偏移。
按照波动方程数字解的方式不同,还可分为有限差分偏移,Kichhoff 积分偏移,有限元法偏移。
按照偏移的算法不同,地震偏移还可分为非递归类偏移(Kichhoff 积分法)和递归类偏移(波长沿拓法偏移)。
Kichhoff 积分法简单、快速,可以处理倾斜地层。但是不能处理低信噪比数据,对速度变化很敏感,不能处理速度横向变化。








 地震偏移处理是地震数据处理的关键步骤,旨在解决水平叠加剖面上的倾斜界面问题,提高空间分辨率和保真度。通过数学算法在计算机上重构地震剖面,使得反射波同相轴归位,改善绕射波和回转波的影响,提供更真实的地下地质结构图像。地震偏移方法包括二维、三维,叠后、叠前,时间、深度偏移等,适应不同的地质复杂性和速度变化情况。叠前深度偏移尤其适用于复杂构造和速度变化大的区域,能提供更精确的成像结果。
地震偏移处理是地震数据处理的关键步骤,旨在解决水平叠加剖面上的倾斜界面问题,提高空间分辨率和保真度。通过数学算法在计算机上重构地震剖面,使得反射波同相轴归位,改善绕射波和回转波的影响,提供更真实的地下地质结构图像。地震偏移方法包括二维、三维,叠后、叠前,时间、深度偏移等,适应不同的地质复杂性和速度变化情况。叠前深度偏移尤其适用于复杂构造和速度变化大的区域,能提供更精确的成像结果。
















 1092
1092

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








