关于坐标下降法(Coordinate Descent)你没理解的事情

概念

• 见下：
  
• 其实就是先固定其他相关变量的值，只对某个未知变量进行优化。

原理

坐标下降法与全局最小值

• 那么问题来了，假如我们寻找到了一个点x使得在所有单个坐标轴上f(x)都最小，是否证明我们找到了全局最小值点？

• 这个问题要分情况来看：

• a. 若f(x)是可微的凸函数，答案是Yes，因为f(x)在任何坐标方向上求偏导都是0，并且对于凸函数来说，局部极小值就是全局最小值：
  

• b. 若f(x)是不可微的凸函数，答案是No，我们可以很容易举出反例，比如下图中算法会在不可微点（右图中红色虚线交叉点）停止迭代，因为在任意坐标方向上f(x)都找不到的更小值了。
  
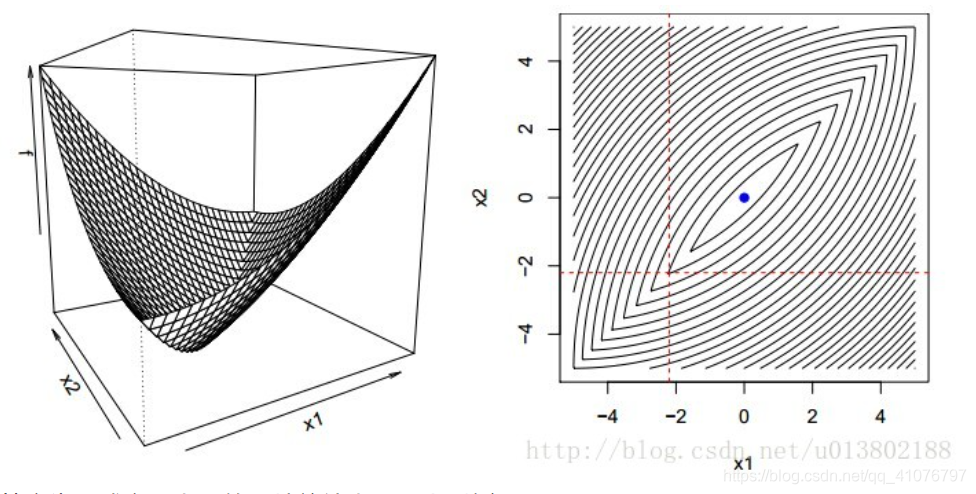
  知道为什么嘛？红点处对应的就是三维图这里的位置：
  
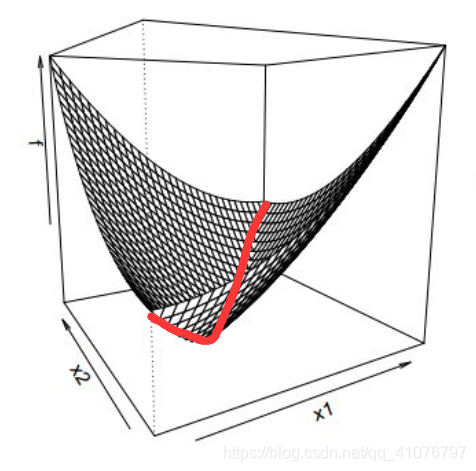
  这个红色的凹槽处任何一点都会导致坐标下降法停止，然而真正的最低点只有一处，不用我说了吧。
  为什么导致坐标下降法停止呢？因为在这条凹槽上的任何一点，你尝试沿着$x_1$，$x_2$方向移动，你发现每个方向都会导致函数值$f(x)$增加，所以坐标下降法认为到达底部了，其实没有。

• c.见下：
  
  
  因为是凸函数，所以有上式中的第一个$>=$符号，你可以随机取两点想象一下。然后又由于$x$是咱们用坐标下降法得到的最终结果，所以在每个维度求和的时候，第一项应当为0 ，即$▽g(x)(y_i-x_i)$中的梯度为0，所以该项=0，而后面一项你要这么理解。首先，每一个$h_i$都是凸函数是什么意思？就是在每个维度上，都增加了一个凹槽，该凹槽是凸函数状的，如图：
  
  上图中的两个红色凹槽分别是平行于两个坐标轴的，他们就是$h_1$，$h_2$，两个凸函数。其实通过b你也能看出来，凹槽存在不可怕，可怕的是存在像b中那样的凹槽，对于两个坐标的增益都是负的，而这里的两个凹槽你可以试一试，不可能出现b中的情况，因为它们的平行于坐标轴的。所以当你真正达到坐标下降法的最低点后，公式中的$h_i(y_i)-h_i(x_i)$必然是正的。

特点

• 坐标轴的顺序可以是任意的，可以使用{1,2,…,n}的任何排列
• 之前我们介绍的是严格的坐标下降法，即每次仅沿着单个坐标轴的方向寻找函数极小值。与之相对应的是块坐标下降法，即每次沿着多个坐标轴的方向（超平面）取极值。
• 将新的
  
• 见下：