本人计算机专业的,本想直接学习顾险峰老师的计算共形几何学课程,但无奈看起来很吃力,于是想补一点基础拓扑学,但是拓扑学又涉及到微分几何,于是找来梁灿彬老师的《微分几何入门与广义相对论》打算拜读前五章,此文章为阅读时的一些笔记。
但是这种书吧不可避免的喜欢先堆一堆的知识而不结合应用,让人看了不知道有啥用,为什么要定义这玩意,看了想睡觉😪 还是找个 视频 看看
连续性
先来点定义。。。
微积分中连续性的定义是这样的: 一元函数 f : R → R 在 x ∈ R 是 C 0 连续 i f ∀ ϵ > 0 ∃ δ > 0 s . t . ∣ x ′ − x ∣ < δ ⟹ ∣ f ( x ′ ) − f ( x ) ∣ < ϵ 一元函数f:\Reals \to \Reals \; 在x \in \Reals是C^0连续\;\; if\; \forall \epsilon >0 \; \exist \delta > 0 \; s.t. \; |x'-x|<\delta \implies |f(x')-f(x)|<\epsilon 一元函数f:R→R在x∈R是C0连续if∀ϵ>0∃δ>0s.t.∣x′−x∣<δ⟹∣f(x′)−f(x)∣<ϵ
映射的连续性定义是这样的: 一元函数 f : X → Y 是 C 0 连续,则 Y 的任何开区间的逆像是 X 的开区间之并 一元函数f: X \to Y \; 是 \; C^0 \; 连续,则Y的任何开区间的逆像是X的开区间之并 一元函数f:X→Y是C0连续,则Y的任何开区间的逆像是X的开区间之并 (逆像就是把y看作自变量,把x看作因变量,两个互换一下)
为什么是开区间之并就连续?这里给出直观的例子说明,严格证明就得自己去找了蛤蛤

图1-2(c) 区间(a’, c’] 是半开区间,不符合连续的定义,不是开区间,所以不连续
逆映射通常只适用于一对一的映射,因为如果是多对一,逆回去的话可能会一对多,但是!
这里定义的逆映射不同,这里的 “逆像”是X的子集而不是X的元素。我来举个例子,比如X中的两个元素x0, x1都映到y0, 因为是集合到集合的映射,所以y0要写作 {y0} ,{y0} 的逆映射就是 {x0, x1}。如果X没有元素映射到y1,那么y1的逆映射是空集,{y0, y1}的逆映射是 {x0, x1}, 是两个集合的并。能够应付对多一对情况。更严谨的说法如下:

FYI:
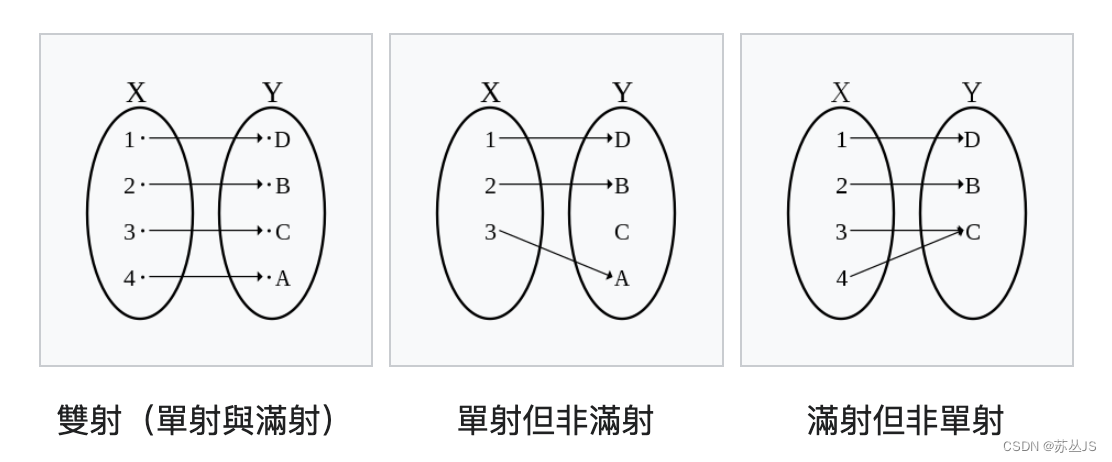
一一映射:双射(既是单射又是满射)
: = := := : 定义号
≡ ≡ ≡: 记作
开子集
我们要对映射 f : R → R f: \Reals \to \Reals f:R→R 连续的定义进行推广,推广到集合(上面其实已经开始用了),因为不是所有的东西都有区间,有区间得有一定顺序。推广的方式是:把 R \Reals R 的任一可以表示为开区间之并的子集称为开子集(open subset,简称open set开集),其它的子集叫做非开子集(切记不叫闭子集吼) 。
对于集合 R \Reals R来说,开子集有三个本质的抽象的(因而便于推广的)性质:
- R \Reals R和空集都是开子集。
- 有限个(不可以无限个)开子集之交仍是开子集(在最后面的练习部分会举一个例子)
- 任意个(可以无限个)开子集之并仍是开子集
(这三个下文会经常提到!)
拓扑空间
- 满足上面三个性质的要求给集合X赋予了一种附加结构,称为拓扑结构。
- 用 P \mathscr{P} P代表由X的全体子集组成的集合,包括开子集和非开子集(X的子集是其中的元素,如图1-3,集合X的一个开子集O在X中是一个圈,在 P \mathscr{P} P中是一个点)
- X的全体开子集也组成一个集合,称为X的一个拓扑,记作
T
\mathscr{T}
T(topology中t的花体大写)
拓扑是开子集的集合,在图1-3中是一个圈。上面的性质一在这里可以写作 X , ∅ ∈ T X, \empty \in \mathscr{T} X,∅∈T。有很多的方式可以选拓扑,但是都必须满足上面三个性质。 - 一个集合可以选不同的拓扑,配上不同的拓扑就形成了不同的拓扑空间。记作 (X,
T
\mathscr{T}
T)、(X,
T
′
\mathscr{T'}
T′),这是两个不同的拓扑空间,因为它们的拓扑不一样即使“底集”X是一样的。

上面的三个性质也可以写成这个样子:


凝聚拓扑
X和空集为开集,其他子集都非开
T = X , ∅ \mathscr{T}={X, \empty} T=X,∅ 这是满足三个性质开集最少的例子
离散拓扑
X的任意子集都是开集
T \mathscr{T} T为X的全部子集的集合(离散空间中,X的每一个子集都是开集,这句话暂时不去深究)
通常拓扑
usual topology
要讨论一个集合是否是开集,首先要明确拓扑。比如凝聚拓扑,它就钦定全集和空集是开集,其它的不管再像也不是开集。一般没有声明是什么拓扑,默认是通常拓扑
诱导拓扑
induced topology

看这个定义是不是有点晕?看个例子吧

看完这个例子再回去看定义会清晰很多。
同胚
说到同胚,先来定义连续。和前面谈到映射的连续差不多,这里只是稍作变形,开区间变成开集:

O是Y的开集,
f
−
1
[
O
]
f^{-1}[O]
f−1[O]表示O的逆映射,也要是开的

一句话就是存在一个映射,一一到上,正反连续。(到上,即满射)
同胚的定义是拓扑空间之间的映射的最高要求,两个互相同胚的拓扑空间已经像得不能再像了,可以视为相等。
练习
- 举一反例证明命题“ ( R , T u ) (\Reals, \mathscr{T_u}) (R,Tu)的无限个开子集之交为开“不真
交集是越交越小,但如果交到最后是空集,倒也还是开的(空集规定为开集),如果无限交到最后变成了一个点或者一堆散点,那么就不开了。一个简单的例子是考虑开区间族 ( − 1 n , 1 n ) ∈ T u , ( n = 1 , 2 , . . . ) (-\frac{1}{n},\frac{1}{n})\in \mathscr{T_u}, \; (n=1,2,...) (−n1,n1)∈Tu,(n=1,2,...) 有限个开子集之交是开的,但是无限个交 ∩ n = 1 ∞ ( − 1 n , 1 n ) \cap_{n=1}^\infty (-\frac{1}{n},\frac{1}{n}) ∩n=1∞(−n1,n1)就退化为 { 0 } \{0\} {0},不开


-
常值映射 f : ( X , T ) → ( Y , S ) f:(X,\mathcal{T})\rightarrow(Y,\mathcal{S}) f:(X,T)→(Y,S)是否连续?为什么?
连续。
常值映射指X上的元素映射到Y上都是同一个元素、一个固定的值(比如一个点),写成符号语言就是: ∀ x ∈ X , x ↦ f ( x ) = y 0 ∈ Y \forall x\in X, x\mapsto f(x)=y_0\in Y ∀x∈X,x↦f(x)=y0∈Y ( ↦ \mapsto ↦表示映射的意思,元素与元素之间的映射)。
复习一下连续的定义:

回到题目。对于 ∀ O ∈ S , 要么 f − 1 [ O ] = ∅ (当 y 0 ∉ O ∈ S ) , 要么 f − 1 [ O ] = X (当 y 0 ∈ O ) \forall O \in S, \;要么\; f^{-1}[O] = \empty(当y_0\notin O\in S), \;要么\; f^{-1}[O] = X(当y_0\in O) ∀O∈S,要么f−1[O]=∅(当y0∈/O∈S),要么f−1[O]=X(当y0∈O) 。因为 ∅ , X \empty, X ∅,X 都是 T \mathcal{T} T 的元素,所以 f − 1 [ O ] ∈ T f^{-1}[O] \in \mathcal{T} f−1[O]∈T,根据连续的定义,这一映射连续。 -
设 T \mathcal{T} T 为集 X X X 上的离散拓扑, S \mathcal{S} S 为集 Y Y Y 上的凝聚拓扑




(偷懒一下,直接放参考答案,里面提到的定义上文都有,习题8指本文的习题2。欢迎讨论)
有什么错误或者疑问可以在评论区留言:)

























 442
442

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








