算法碎碎念之双光配准算法

配准算法

双光配准的误差分析

双光融合通常是对可见光和红外进行像素级融合，以达到信息互补的目的。但是往往图像来源是多模态、多视角的，需要对图像进行对齐。

首先，不同相机的焦距、视场角不一样，导致单位像素代表的实际场景的物理尺度也不一样。通常可以通过焦距的比例进行初步校正：

$S_x=f_{vi,x}/f_{ir,x},S_y=f_{vi,y}/f_{ir,y}$；

$widt{h}_{ir,new}=widt{h}_{ir}\ast S_x,heigh{t}_{ir,new}=heigh{t}_{ir}\ast S_y$ 。

通过这一公式，像素上的物理尺度基本可以达成一致。

‍

再往后分析，就是相机的旋转和平移。

这方面的计算方法比较多，可以用红外热标定板取角点，通过最小二乘法拟合，可以单独分开计算旋转和平移，也可以直接拟合仿射矩阵。或者对于单独的图像对，直接手动取点，手动计算，边缘滤波+模板匹配等。如果不要求工业应用，直接手动一点一点调也可以，效果都差不太多。

然后把参数使用到现实场景，就会发现，怎么没对齐？特别是左右方向有大小不一的重影，距离相机越近，误差越大。

原因在于视差。

如果做过双目立体视觉的就比较容易理解，毕竟双目测距就是通过左右视差来计算，但是在配准上，视差就是大麻烦。如果不是多视角融合，就不会存在这个问题，如多曝光融合等。

简单的解释：
​

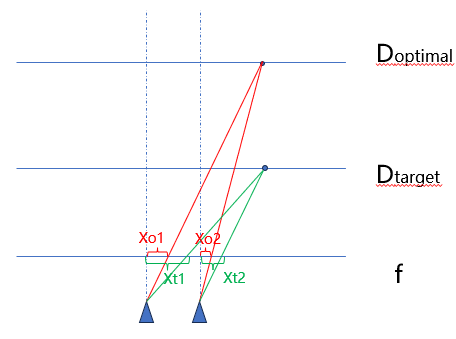
如上图，两个物体分别位于$D_{optimal}、D_{target}$，在两个相机的焦平面上生成的像素点的偏移距离分别是$x_{t1}-x_{t2},x_{o1}-x_{o2}$且不相等。假设$D_{target}$是标定平面，$x_{t1}-x_{t2}$是标定的参数。在实际场景上却在$D_{optimal}$，那么对齐误差为$(x_{o1}-x_{o2})-(x_{t1}-x_{t2})$。而通常我们相机是左右放置，所以在垂直方向误差基本可以忽略。

将这一情况的误差用数学语言表达：

$$\begin{array}{rl}{\delta }_x& =(x_{o1}-x_{o2})-(x_{t1}-x_{t2})\\ & =(x_{t2}+d_c-x_{t1})-(x_{o2}+d_c-x_{o1})\\ & =\frac{d_c}{D_{target}}\ast (D_{target}-f)-\frac{d_c}{D_{optimal}}\ast (D_{optimal}-f)\\ & =f\ast d_c\ast (\frac{1}{D_{optimal}}-\frac{1}{D_{target}})\\ & =\frac{f\ast d_c}{l_{pix}}\ast (\frac{1}{D_{optimal}}-\frac{1}{D_{target}})\\ & =f^{\prime }\ast d_c\ast (\frac{1}{D_{optimal}}-\frac{1}{D_{target}})\end{array}$$

$d_c$表示相机光轴间距，$f$表示物理焦距，$f^{\prime }$表示像素焦距（pix/mm），$l_{pix}$表示单位像素的大小。

所以从公式我们可以解释配准时的一些现象，如左右出现误差的方向不一样，远处的误差小，近处的误差大等。

‍

有学者根据这一公式提出误差补偿：Fast and accurate calibration-based thermal / colour sensors registration 。

除此之外，还有通过变形场进行实时校正、实时计算仿射矩阵进行校正等方法。

‍

‍

配准对齐思路

配准思路：全局配准、局部配准

有的论文将全局配准描述为粗配准、局部配准为精细配准。全局配准通过单应性变换对全图进行对齐，这种对齐是粗略的，因为不同的深度视差会导致前景后景的不匹配，这不是一个单应性变换可以解决的。于是更进一步是局部对齐和更进一步的像素对齐。

局部对齐的思路就是对不同深度的图像块计算不同的单应性变换，再通过插值等方法进行全局变换。

更进一步像素对齐多指深度学习方法计算的逐像素位移变形场。

‍

全局对齐和局部对齐都有两条路，传统的流程较为固定：特征检测-特征匹配-单应性计算。根据特征检测和匹配的方法不同衍生出各种算法（SIFT、SURF、ORD、RIFT等）；深度学习的方法则是将传统的流程部分或全部所有深度学习模型来实现，全流程的Deep Homography（https://arxiv.org/abs/1606.03798）、特征提取与匹配的Patch2Pix（https://openaccess.thecvf.com/content/CVPR2021/papers/Zhou_Patch2Pix_Epipolar-Guided_Pixel-Level_Correspondences_CVPR_2021_paper.pdf）等。

局部对齐主要集中在网格变形方法上，传统的方法是结合特征匹配，在全局对齐的基础上对图像细分。根据在局部图像块上的特征匹配情况进行局部单应性计算，再映射到全局，如APAP、Meshflow算法。深度学习的方法则是端到端地计算局部端点的位移量，如Deep MeshFlow将Deep Homography的4个位移量扩展为网格端点位移量的计算，对于双平面场景提出的前景后景通过mask分开计算的dual-homography等 。

像素级对齐只针对深度学习的方法，端到端地计算出每个像素地位移，构造变形场。

‍

在工程上关注的的是稳定性、实时性、可移植性。对于局部配准，则比较难满足这一要求，首先局部配准的计算量相比较全局配准会上升，其次，局部配准涉及到逐帧计算，实时性是一个方面，另一个方面是帧间变形的稳定性。全局配准可以在相对固定的场景使用一个单应变换，因为全局配准必然是“配不准”的，它允许一定的误差。而局部配准就是为了消除这一部分误差而研究的，因此必然需要每一帧都计算一个变形场，那么每一帧的变形场都是在变化的，这会造成视频画面的晃动，这就有点类似电子稳像的内容，还要保证帧间的变化足够流畅和稳定。因此在工程上更多地考虑更好的全局对齐。

‍

‍