CURE算法详解

写在前面

CURE作为一种针对大数据的聚类方法，其在内存管理的思路上和BFR思路类似,具体可以稍微看一下前面的文章。
具体可以参考原论文

---

凝聚和分裂层次聚类

1、凝聚的层次聚类：AGNES算法 (AGglomerative NESting)==>采用自底向上的策略。最初将每个对象作为一个簇，然后这些簇根据某些准则被一步一步合并，两个簇间的距离可以由这两个不同簇中距离最近的数据点的相似度来确定；聚类的合并过程反复进行直到所有的对象满足簇数目。

2、分裂的层次聚类：DIANA算法 (DIvisive ANALysis)==>采用自顶向下的策略。首先将所有对象置于一个簇中，然后按照某种既定的规则逐渐细分为越来越小的簇(比如最大的欧式距离)，直到达到某个终结条件(簇数目或者簇距离达到阈值)；

其他聚类算法的缺陷

基于划分聚类算法的缺陷：
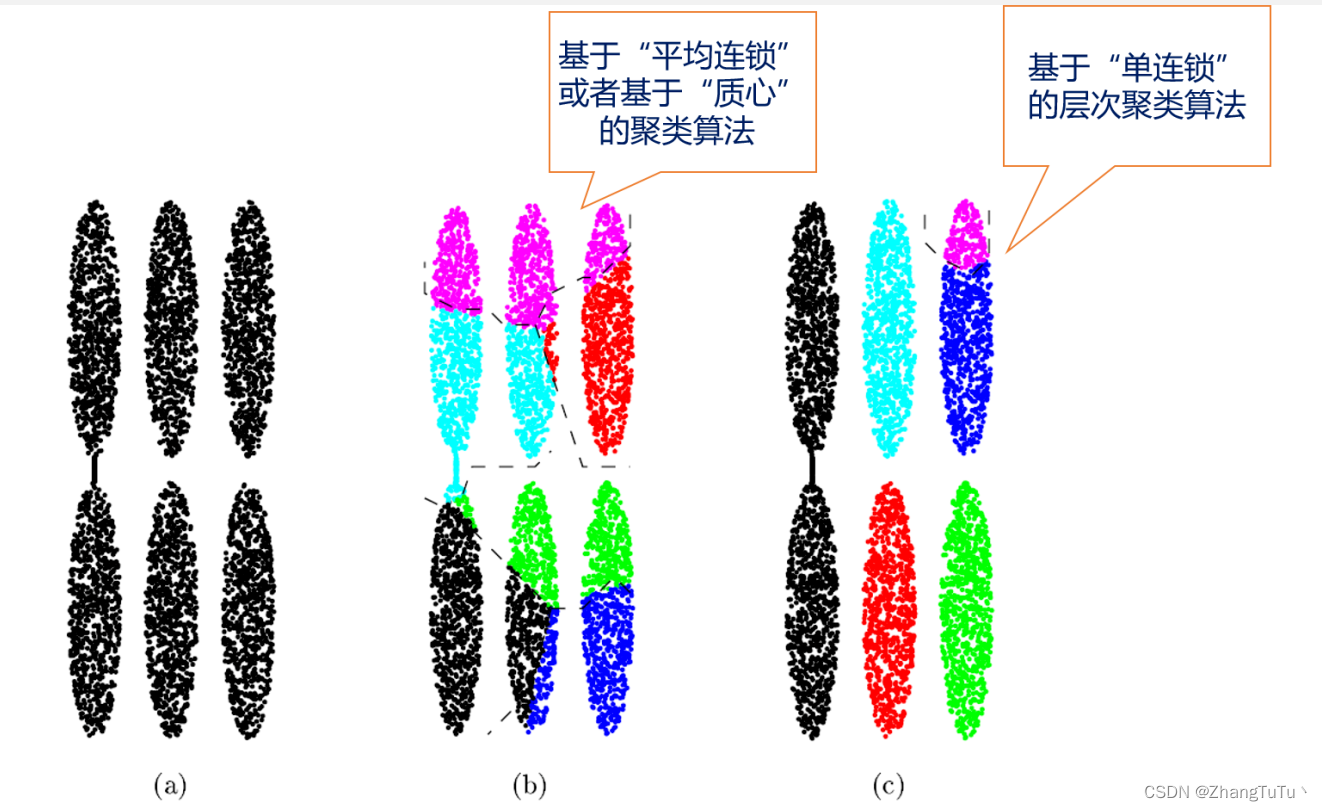
基于划分的聚类算法比如Hierarchical K-means聚类算法，不能够很好地区分尺寸差距大的簇，K-means算法基于“质心”加一定“半径”对数据进行划分，导致最后聚类的簇近似“圆形”。

基于“平均连锁”或者基于“质心”的簇间距离计算方式得到的聚类结果，可以看出，聚类结果同基于划分的聚类算法相似、最后聚类的结果呈“圆形”，不能够准确地识别条形的数据；（c）图使用的是基于“单连锁”的簇间距离计算策略，由“单连锁”的定义可知，对于（c）图中最左边两个由一条细线相连的两个簇，会被聚类成一个簇，这也不是我们想要的。

CURE

CURE算法(使用代表点的聚类法)：是一种凝聚算法(AGNES)。该算法先把每个数据点看成一类，然后合并距离最近的类直至类个数为所要求的个数为止。但是和AGNES算法的区别是：取消了使用所有点或用中心点+距离来表示一个类，而是从每个类中抽取固定数量、分布较好的点作为此类的代表点，并将这些代表点(一般10个)乘以一个适当的收缩因子(一般设置0.2~0.7之间)，使它们更加靠近类中心点。代表点的收缩特性可以调整模型可以匹配那些非球形的场景，而且收缩因子的使用可以减少噪音对聚类的影响。

具体流程

1 .对于较大规模的数据，首先对整个样本进行采样，原论文中采样方式使用了随机采样算法

作者在论文中明确表示了采样方法的正当性即中等大小的随机样本相当准确地保存了关于簇几何结构的信息，从而使CURE能够正确地对输入进行聚类

2. 对上面采样出来的数据，使用传统的聚类算法(比如层次聚类)，进行聚类，形成初步的聚类结果;

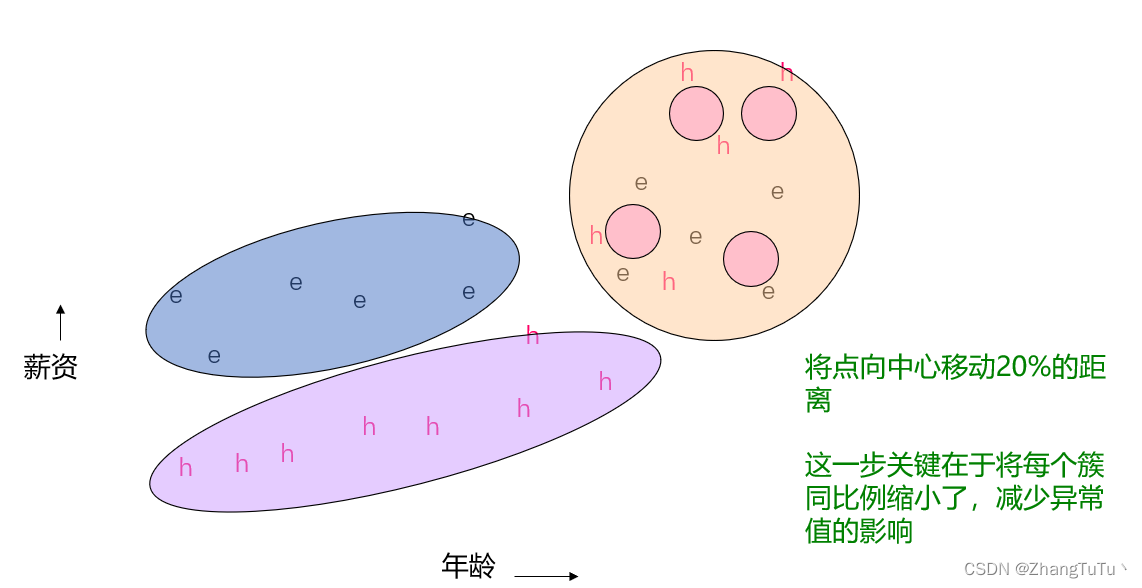
3. 接下来一步很关键–寻找一系列的代表点(representative points)：对于上一步聚类出来的每个组，我们在每个组内选择k(比如4)个点，这四个点要尽可能尽可能尽可能地分散在这个组内，尽可能地覆盖到整个组；做法类似随机在组内选取一个离中心点最远的点，第二点要是组内所有点离第一个点最远的点，第三个点要是组内所有点离第一第二个点最远的点，以此类推；这一步的作用是尝试找到每个组的形状，定义每个组的模样；

4. 我们把每个组内的所有代表点，每一个代表点都按照固定百分比(比如20%)向各自组内的中心点移动一段距离，例子如下；这一步关键在于将每个簇同比例缩小了，减少异常值的影响

5. 接下来，重新扫描所有的数据， “最近的簇”对于点$p$，使用如下公式，找到距离p最近的簇：
   $p_{closest}=min(dist(p,C_i))$
   $dist(p,C_i)=min||p-p^{\prime }||$
   为每一个点$p$找到其最近簇，并将该点$p$置于最近簇中。

原文中关于随机采样的描述
Random Sampling and Partitioning: CURES approach tothe clustering problem for large data sets differs from BIRCHin two ways. First, instead of preclustering with all the datapoints, CURE begins by drawing a random sample from thedatabase. We show, both analytically and experimentally,that random samples of moderate sizes preserve information about the geometry of clusters fairly accurately, thusenabling CURE to correctly cluster the input. In particular, assuming that each cluster has a certain minimum size,we use chernoff bounds to calculate the minimum salsize for which the sample contains, with high probability,at least a fraction f of every cluster. Second, in order tofurther speed up clustering, CURE first partitions the random sample and partially clusters the data points in eachpartition. After eliminating outliers, the preclustered datain each partition is then clustered in a final pass to generate the final clusters.

随机采样和分区：CURES方法在两个方面不同于BIRCH方法。首先，CURE不是对所有数据点进行预聚类，而是从数据库中随机抽取一个样本。我们通过分析和实验表明，中等大小的随机样本相当准确地保存了关于簇几何结构的信息，从而使CURE能够正确地对输入进行聚类。特别是，假设每个簇都有一定的最小大小，我们使用chernoff边界来计算样本包含每个簇的至少一部分f的最小salsize，这很有可能。其次，为了进一步加快聚类，CURE首先对随机样本进行分区，并对每个分区中的数据点进行部分聚类。在消除异常值之后，每个分区中的预聚类数据然后在最后一个过程中进行聚类，以生成最终的聚类。

论文中给出的具体步骤

结尾

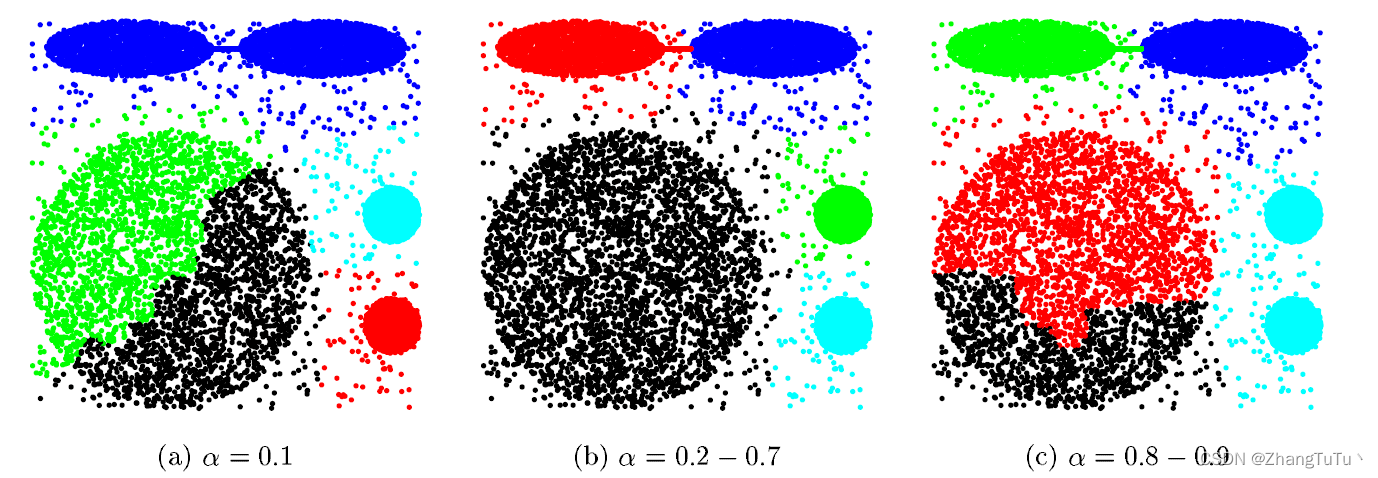
收缩系数α的取值不同，聚类结果也相应不同。当$\alpha$趋于0时，所有的“代表点”都汇聚到质心，算法退化为基于“质心”的聚类；当$\alpha$趋于1时，“代表点”完全没有收缩，算法退化为基于“全连接”的聚类，因此$\alpha$值需要要根据数据特征灵活选取，才能得到更好的聚类结果：