（四）平面图与着色——图论笔记系列

4，平面图与着色

4.1，平面图

定义：把G画在平面上，使得除了顶点外，任意两条边不交叉，称G可嵌入平面，G为平面图。

性质：一个平面图G把平面分成若干连通片，这些连通片称为G的区域，或G的一个面。其中有界区域称为内部面或有界面；无界区域称为外部面或无界面。G的面组成的集合用Φ表示。

边界：每个面所有边构成的回路；

面的度数（次数）：面的边界的长度，即为d（R）

极大平面图

定义：若在任意两个不相邻 的结点vi,vj之间加入边{vi,vj}，就会破坏图的平面性，则称G是极大平面图。

定理：

1. 有限平面图中，所有面的次数之和等于边数的2倍。
2. 欧拉公式：任意连通平面图G，若有n个结点，m条边和r个面，则欧拉公式n-m+r=2成立。

欧拉公式的推论1：

比如：证明$K_5$是非平面图。

因为，由推论1知：$K_5$有5个顶点10条边，而3*5-6=9<10;不满足条件。

欧拉公式的推论2：

证明略（提示：G的每一个面的度数至少为4）。

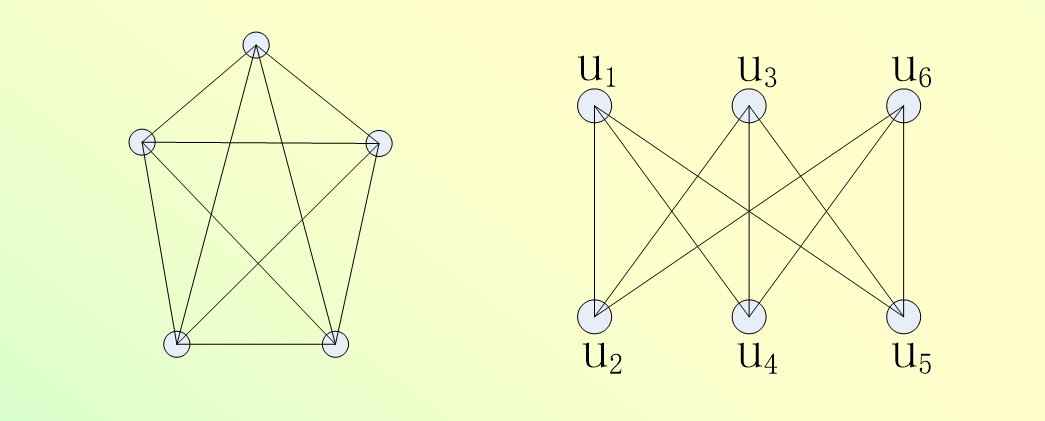
比如：证明$K_{3,3}$是非平面图。

因为K33中没有长度为3的圈，每个面的度数至少为4。所以9 >2*6-4,不满足条件。

判定：

定义：

2度顶点内扩充：在图G的边上插入一个2度顶点，使一条边分成两条边，称将图在2度顶点内扩充；

2度顶点内收缩：去掉一个图的2度顶点，使关联它们的两条边合并成一条边，称将图G在2度顶点内收缩。

同胚：两个图G1和图G2，若图G1和图G2同构，或者通过多次在2度点内扩充或者收缩，

​ 它们能够同构，则称图G1和图G2是同胚的。

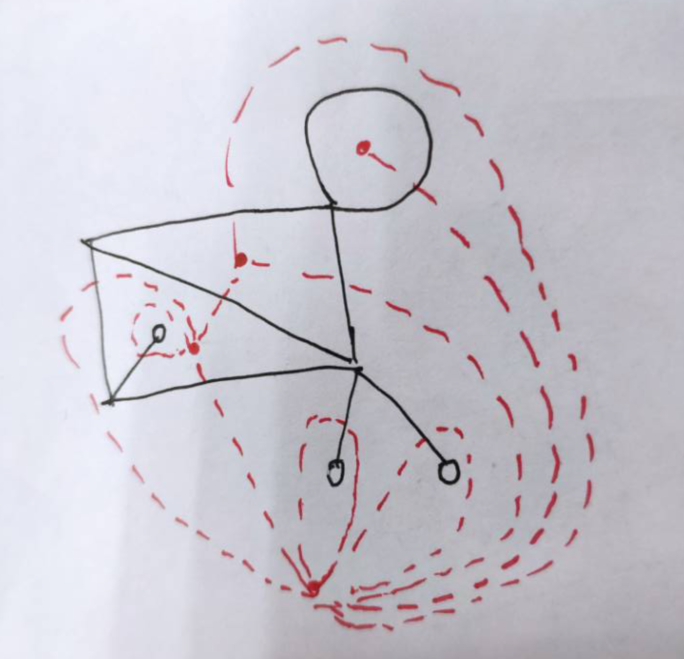
4.2，对偶图

任何一个平面图都有一个与之对应的平面图，称之为对偶图。

4.3，图的着色

4.4，图的色多项式

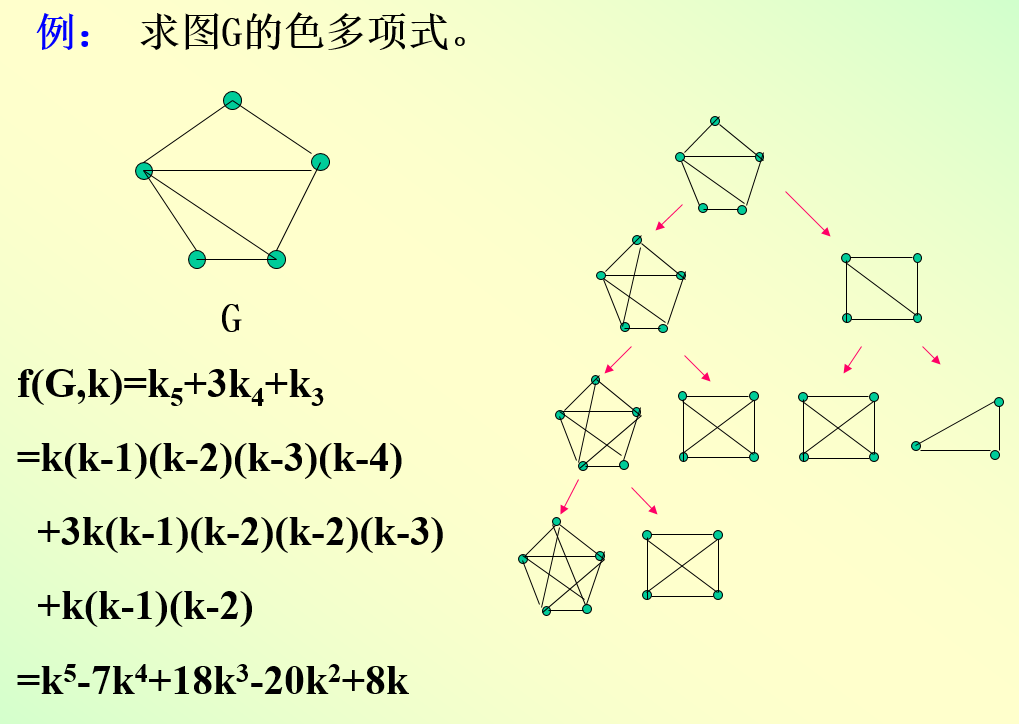
定义：图G的不同K-可着色的数目称为图G的色多项式。记作f(G,k).

对三阶完全图K3而言,有f(K3,k)=k(k-1)(k-2)。

一般地,有f(Kp,k)=k(k-1)(k-2)…(k-p+1)。

也就是说，对于一个色多项式可以按照多一条边+少一个顶点的方式进行拆分，直到所得子图都是完全图为止。

根据色多项式求色素数：

$f(G,k)=f(K_{n1},k)+f(K_{n2},k)+...+f(K_{nr},k)$,其中，λ(G)=min{n1,n2,…,nr}。