numpy中矩阵相乘和矩阵点乘

最新推荐文章于 2025-03-09 12:39:26 发布
最新推荐文章于 2025-03-09 12:39:26 发布
阅读量3.2k 收藏 24
点赞数 5
分类专栏： python 文章标签： numpy
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_41618091/article/details/96863765
版权

矩阵相乘

条件：左矩阵的列数等于右矩阵的行数

操作：同线性代数中矩阵乘法

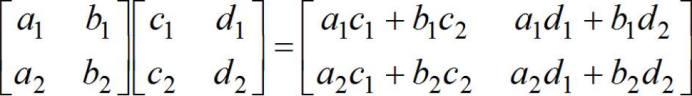
当使用np.array()定义矩阵时，a,b矩阵相乘：np.dot(a,b)

当使用np.mat()定义矩阵时，a,b矩阵相乘：np.dot(a,b)或a*b

矩阵点乘

条件：同型矩阵（两矩阵行数和列数相同）

操作：同位置元素相乘

当使用np.array()定义矩阵时，a,b矩阵点乘：a*b或np.multiply(a,b)

当使用np.mat()定义矩阵时，a,b矩阵点乘：np.multiply(a,b)

注意：python的numpy有广播机制，所以在使用numpy库的过程中，矩阵点乘的条件（同型矩阵）可以不满足。需满足下图General Principle(通用规则)可以使用广播机制:

下图为矩阵点乘时广播机制的使用

Numpy实现矩阵的加、减、点乘、叉乘、求逆
weixin_61269526的博客
03-21 1403
Numpy实现矩阵的加、减、点乘、叉乘、求逆。
python 矩阵点乘_python相乘矩阵
weixin_39593277的博客
11-29 1550
广告关闭腾讯云11.11云上盛惠 ，精选热门产品助力上云，云服务器首年88元起，买的越多返的越多，最高返5000元！鉴于最近复习线性代数计算量较大，且1800答案常常忽略一些逆阵、行列式的计算答案，故用python写出矩阵的简单计算程序，便于检查出错的步骤。 1、行列式 可自行更改阶数from numpy import * # 求行列式 ,建议：取小数点前整数 a = array(, , , ])...
【NumPy】矩阵乘法与点乘
Spade_的博客
02-11 1万+
1. Numpy.dot() 一维矩阵：计算内积 dot( 1 x n , 1 x n ) = 一个数 二维矩阵：线性代数矩阵相乘(n x m)·(m x s) dot( n x m , m x s ) = n x s import numpy as np # 1. 一维矩阵：计算内积 # 1 x 3 one_and_three_a = np.array([1, 2, 3]) ...
Matlab:矩阵运算篇——矩阵数学运算
m0_71824048的博客
03-09 1247
设都是m*n矩阵，矩阵A和B的和记成A+B，规定为。（1）交换律 A+B=B+A(2)结合律 （A+B）+C=A+（B+C）
numpy中的乘法：点乘，矩阵乘法
wugou2014的博客
03-10 963
详细解释了numpy中的乘法，包括向量乘法，矩阵乘法，向量与矩阵的乘法
numpy中矩阵的点乘和叉乘
kjhupupup的博客
04-26 4067
点乘：两个矩阵对应位置的元素相乘，且这两个矩阵行数列数相等 import numpy as np a=np.array([[1,2,3],[1,2,3],[1,2,3]]) b=np.array([[1,2,3],[1,2,3],[1,2,3]]) print(a*b) print(np.multiply(a,b)) [[1 4 9] [1 4 9] [1 4 9]] [[1 4 9] [1 4 9] [1 4 9]] 叉乘：就是线性代数的矩阵乘法 import numpy as np a=np.array
Numpy中的两种矩阵乘法和两种点乘
塞上江南的专栏
02-05 5283
1. 矩阵乘法：对于结果矩阵中的每一个元素，其值等于第一个矩阵中该元素所在的行与第二矩阵中该元素所在的列相乘并求和； 2. Numpy中的两种矩阵乘法：Numpy.dot(a,b)和运算符 ‘@’； 两种点乘：Numpy.multiply(a,b)和*； 3. 例1：a = np.array([1,2,3]); b =np.array([1,2,3]); c = n.dot(a,b); d = np.multiply(a,b); e = a@b; f = a*b; 结果：c = e = 14...
使用Numpy/TensorFlow中的tensordot进行多维矩阵相乘
blueorris的专栏
04-14 2615
在使用tensordot进行矩阵相乘的时候，axes是一个重要的参数，它可以定义两个矩阵互乘的时候是使用内积、外积、或是其他方法。 以TensorFlow的tensordot为例，其语法为： tf.tensordot( a, b, axes, name=None ) 其中a和b为输入的两个矩阵，参数axes定义了两个矩阵如何相乘。 如设置“axes=0”的时候，相当于定义为算a和...
Python矩阵相乘
热门推荐
Dfreedom.的博客
09-25 3万+
叉乘就是矩阵的乘法，指矩阵A的第一行乘以矩阵B的第一列，各个元素对应相乘后求和作为第一个元素的值。能够进行叉乘运算的场景：A的行数等于B的列数。矩阵的点乘就是矩阵A和矩阵B各个对应元素的相乘。能够进行点乘运算的场景：①A和B的行向量个数相等；② A和B的列向量的个数相等；③ A和B的行向量和列向量都相等。在matlab里面实现点乘用“.*”，实现叉乘用“*”，非常清晰明了。但是在Python里面实现矩阵相乘时经常会报错，原因是在Python里面向量和矩阵的概念和数学里面的概念有点差异。
Python之numpy库——矩阵相乘
浮沉随浪。
04-10 2万+
在机器学习中，会遇见两个矩阵并非向量乘积，而是数值上的相乘。当下我是初学者，遇见后很困惑，于是搜索了相关资料，写个文章，总结一下个人理解。 后续会进行更新，我是用到哪些就查哪些，就总结哪些 一、 向量的点乘 也叫向量的内积、数量积，对两个向量执行点乘运算，就是对这两个向量对应位一一相乘之后求和的操作，点乘的结果是一个标量。 1、设n1是3 x 3 的矩阵，n2 是1 x 3 的矩阵 如上图所示...
Numpy实现矩阵点乘和乘积运算
u010447762的博客
08-15 285
搞清楚Numpy如何实现矩阵的点乘和乘积运算 矩阵点乘：对位相乘，矩阵形状必须相同（单行单列矩阵适用广播机制复制后形状也相同） 矩阵乘积：行与列对位相乘再相加，第一个矩阵的列与第二个矩阵的行必须相等才能进行运算。
python 矩阵点乘_Python之Numpy库基础——矩阵运算
weixin_39577964的博客
01-10 1万+
在学习线性代数时我们所接触的矩阵之间的乘法是矩阵的叉乘，有这样一个前提：若矩阵A是m*n阶的,B是p*q阶的矩阵,AB能相乘,首先得满足：n=p，即A的列数要等于B的行数。运算的方法如下图：当时学线性代数时老师教的更为直观记法：点乘则是这样：假如有a，b两个矩阵，在Matlab中我们实现点乘和叉乘的方式分别如下：a.*b %表示点乘 a*b %表示叉乘下面我们来看看python中的操作：impor...
Python_Numpy库中各种矩阵基本运算(加、减、乘、点乘、点除、乘方、转置等)
昊虹AI笔记
06-12 2万+
Python的Numpy库中各种矩阵基本运算的示例代码
NumPy矩阵乘法
ccc369639963的博客
04-15 1万+
NumPy矩阵乘法 矩阵乘法是将两个矩阵作为输入值，并将 A 矩阵的行与 B 矩阵的列对应位置相乘再相加，从而生成一个新矩阵，如下图所示： 注意：必须确保第一个矩阵中的行数等于第二个矩阵中的列数，否则不能进行矩阵乘法运算。 图1：矩阵乘法 矩阵乘法运算被称为向量化操作，向量化的主要目的是减少使用的 for 循环次数或者根本不使用。这样做的目的是为了加速程序的计算。 下面介绍 NumPy 提供的三种矩阵乘法，从而进一步加深对矩阵乘法的理解。 逐元素矩阵乘法 multiple() 函数用于两个矩阵的逐元素乘法
python中两个矩阵之间的点乘_Python基础--数据分析库--Numpy
weixin_39598135的博客
11-22 1196
一、基础概念NumPy(Numerical Python) 是 Python 语言的一个扩展程序库，支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库。NumPy 通常与 SciPy(Scientific Python)和 Matplotlib(绘图库)一起使用， 这种组合广泛用于替代 MatLab，是一个强大的科学计算环境，有助于我们通过 Python 学习数据科学或者机器学习...
向量和矩阵运算及Numpy中对应方法
博客简介
06-18 2065
向量的内积等价于a@b向量的外积向量元素对应位置相乘等价于a*b矩阵点乘np.multiply(a,b)等价于a*b矩阵叉乘等价于a@b。
【机器学习-02】矩阵基础运算---numpy操作
2201_75604341的博客
04-01 638
学好 Python 不论是就业还是做副业赚钱都不错，但要学会 Python 还是要有一个学习规划。最后大家分享一份全套的 Python 学习资料，给那些想学习 Python 的小伙伴们一点帮助！
python-数据分析（8-numpy02）
zaibiketaide的专栏
09-07 853
Numpy 8 Numpy02 8.1 Numpy数组算术 数组之所以重要是因为它允许我们进行批量操作数据并且没有任何for循环。也被称为向量化。 数组与标量的算术操作 数组与标量的算术操作会把计算参数传递给数组的每一个元素。 import numpy as np arr = np.arange(6).reshape(2,3) arr+1 -------------------- array([[1, 2, 3], [4, 5, 6]]) 两个等尺寸数组的算术操作 两个等尺寸数组的算术操作实
numpy dot矩阵和向量相乘
最新发布
03-29
### 使用 NumPy 的 `dot` 函数实现矩阵与向量的点乘 在数据科学领域，矩阵运算非常常见。当涉及到矩阵与向量之间的点乘操作时，可以利用 NumPy 提供的强大功能来完成这一任务。具体来说，可以通过调用 `np.dot()` 或者 `.dot()` 方法来进行计算。 以下是关于如何使用 NumPy 进行矩阵与向量点乘的具体说明： #### 基本概念 矩阵与向量的点乘实际上是通过一系列矢量间的点积（dot product）来定义的。对于一个 \( m \times n \) 大小的矩阵 \( A \)，以及长度为 \( n \) 的列向量 \( v \)，它们的结果是一个大小为 \( m \) 的列向量[^4]。 #### 实现方法 NumPy 中提供了多种方式执行矩阵与向量的点乘操作，其中最常用的是 `np.dot(A, v)` 和 `A.dot(v)`。这两种形式的功能完全一致，可以根据个人习惯选择其中之一。 下面展示了一个具体的例子，演示如何使用 `dot` 函数进行矩阵与向量的点乘操作： ```python import numpy as np # 定义一个 3x2 矩阵 A A = np.array([[1, 2], [3, 4], [5, 6]]) # 定义一个长度为 2 的列向量 v v = np.array([7, 8]) # 计算矩阵 A 与向量 v 的点乘结果 result_dot = np.dot(A, v) print(result_dot) ``` 运行上述代码后，得到的结果将是 `[23, 53, 83]`，这正是矩阵每行分别与向量相乘并求和后的结果。 需要注意的一点是，在某些情况下如果希望更直观地表达矩阵乘法而非逐元素相乘，则可以选择使用 `numpy.matrix` 类型替代默认数组类型。此时简单地运用星号 (`*`) 即可表示矩阵乘法[^2]。 然而值得注意的是，尽管 `numpy.matrix` 可以为特定场景提供便利，但由于其兼容性和灵活性较差的原因，官方文档建议优先采用常规 ndarray 结合相应函数的方式处理大多数线性代数需求[^1]。 #### 总结 综上所述，借助于 NumPy 库中的 `dot` 函数能够高效便捷地达成矩阵同向量之间点乘的目的，并且推荐按照标准做法即基于 ndarray 来构建输入数据结构以便获得更好的通用支持效果。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值