卫星绕地运动受到的各种力影响着卫星的运动状态，由于受到的力多，所以它运动的轨迹就非常复杂，很难用简单、精确的数学模型表示出来。GPS定位要知道卫星的具体位置，所以要进行高精度的相对定位，就必须研究卫星轨道的运动规律。
一、前言
卫星在空间运行的轨迹称为轨道描述卫星轨道位置和状态的参数称为轨道参数，开普勒轨道参数是用于描述卫星轨道。
卫星在空间绕地球运行时，除了受地球重力场的引力作用外，还受到太阳、月亮和其它天体的引力影响，以及太阳光压、大气阻力和地球潮汐力等素影响。
影响卫星运动的天体引力分为两类：地球质心引力 (中心引力)和摄动力(非中心引力仅为10量级)
（1）地球质心引力 (中心引力)：密度均匀或由无限多密度均匀的同心球层所构成的圆球，称之为二体问题，卫星运动模型为二体模型。
（2）摄动力(非中心引力仅为10量级)：非球形对的地球引力，日、月引力大气阻力太阳光压,地球潮汐力等(各作用力均小于10)
GPS卫星的无摄椭圆轨道运动就是用开普勒轨道参数来描述。
卫星运动分为两类：无摄运动和受摄运动
通常分为两步地球在中心力的作用下的卫星运动称为无摄运动，用以描述卫星的基本特征。
在摄动力的作用下的卫星运动称为受摄运动，相应的卫星轨道称为受摄轨道，用以确定卫星受摄运动轨道的瞬时特征。
二体问题下的卫星运动虽然是一种近似描述，但能得到卫星运动的严密分析解，从而可以在此基础上再加上摄动力来推求卫星受摄运动的轨道。
２、卫星的无摄运动
卫星发射升至预定高度后，开始绕地球运行。假设地球为均质球体，根据万有引力定律，卫星的引力加速度为
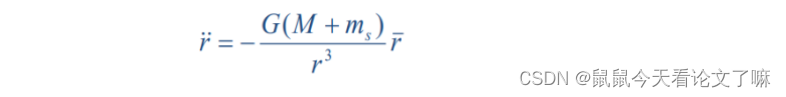
其中，G为引力常数，M为地球质量，m为卫星质量，r为卫星的地心向径
引力加速度决定了卫星绕地球运动的基本规律，依据以上公式研究天体运动中的卫星运动问题，称为二体问题；
卫星在上述引力场中运动，称为无摄运动，又称为开普勒运动，能够用开普勒定律描述。
二、开普勒三大行星定律
1.卫星运动的轨迹为椭圆，椭圆的一个焦点与地球质心重合；
2.卫星的地心向径在单位时间内所扫过的面积相等；此定律说明行星离太阳越近，其运行速率越大。
3.卫星运行周期的平方与轨道椭圆长半径的立方之比为一常量，等于GM的倒数。
卫星轨道周期的平方正比与椭圆轨道半长轴的立方。
使用能量守恒定理和开普勒第三定理，可以推导卫星的轨道周期T为
T
=
2
π
a
3
/
μ
.
\ T = 2π \sqrt{a^3/μ}\,.
T=2πa3/μ.
其中，a是半长轴，开普勒常数
μ
=
3.9861
∗
1
0
5
k
m
3
/
s
2
μ = 3.9861*10^5km^3/s^2
μ=3.9861∗105km3/s2
椭圆轨道卫星具有时变的在轨飞行速度：
v
=
μ
(
2
r
−
1
a
)
(
k
m
/
s
)
v=\sqrt{μ(\frac{2}{r}-\frac{1}{a})} (km/s)
v=μ(r2−a1)(km/s)
在远地点和近地点的速度分别为
v
a
=
μ
r
p
a
r
a
v_a=\sqrt{\frac{μr_p}{ar_a}}
va=araμrp
v
p
=
μ
r
a
a
r
p
v_p=\sqrt{\frac{μr_a}{ar_p}}
vp=arpμra
圆轨道卫星具有恒定的速度：
v
=
μ
a
v=\sqrt{\frac{μ}{a}}
v=aμ
三、开普勒轨道参数
3.1 轨道六根数
开普勒轨道参数包含6个参数：轨道升交点赤经、轨道倾角、近地点角距、长半径、偏心率和真近点角。
| 升交点经度（赤经Ω） | Longitude of Ascending Node of Orbit Plane | 指卫星沿轨道从地球南极向北运动时与地球赤道面的交点。此交点的经度即为升交点经度，或者赤经 |
| 轨道半长轴（a） | Semi-Major Axis of Orbit | 指卫星椭圆轨道长轴的一半，有时可以认为是平均轨道半径 |
| 轨道偏心率（e） | Eccentricity | 为椭圆扁平程度的一种量度，定义是椭圆两焦点间的距离与长轴长度的比值 |
| 近地点幅角（角距ω） | Argument of Perigee | 航天器绕地球运行的椭圆轨道上距地心最近的一点。近地点幅角是指轨道近地点与升交点之间对地心的张角。沿卫星运动方向从升交点量测到近地点，取值范围为0°-360° |
| 轨道倾角（i） | Inclination Angle | 行星轨道面对赤道面的倾角；在升交点处从赤道面逆时针方向量到行星轨道面的角度 |
| 真近点角（V） | True Anomaly | 平近点角（Mean Anomaly）基于一个虚拟的圆形运转轨道，其作用是提供一个数据，可以用于快速比较轨道上运动物体不同时刻的相对位置距离。其定义如下，考虑一个天体的开普勒轨道，即一个椭圆轨道，在其之上运转的物体一周所需时间为T，则其平均运动角速度为v=2π/T，以其近拱点2 为0度位置，若t0时刻物体在近拱点，则t时间后，其平近点角M的值为v（t-t0）。注意，平近点角不是物体的真实位置角度，是运转在虚拟圆形轨道上的（以椭圆轨道长轴中点为圆心，半长轴为半径的辅助圆），根据定义，在此圆上速度匀定，所以不同时刻的位置距离正比与时间间隔，这极大简化了位置比较所需的计算需求。真实体现物体实际位置角度的参数被称为真近点角. |
要想确定卫星的位置，首先要确定卫星运行轨道所在平面的位置。卫星轨道平面通过地心，与赤道面相交，其夹角就是轨道倾角。卫星轨道在轨道平面内，卫星沿着轨道由南向北运行时与赤道面的交点称为卫星赤道升交点，简称升交点。此升交点在赤道面内与春分点对地心的夹角即为轨道升交点赤经。有了轨道倾角和轨道升交点赤经，就可以确定卫星轨道平面相对赤道面的位置。
轨道平面确定后，需要确定轨道椭圆。近地点角距用于确定椭圆方位，它是近地点在轨道平面内与升交点相对地心的夹角，确定了轨道椭圆长轴的方向。再加上长半径和偏心率，椭圆在轨道平面内的位置就确定下来了。最后一个参数真近点角用于确定卫星在轨道椭圆上的相对位置，它定义为卫星当前位置在轨道平面内与近地点相对地心的夹角。于是通过这一套开普勒轨道参数，卫星相对赤道的空间位置就确定了。
卫星在太空中运动，受到各种天体的万有引力，如果要考虑所有星体的万有引力，那么情况将变得超级超级复杂。为了使得问题得到简化（即使在损失一定精度的情况下），仅仅考虑地球和卫星之间的相互作用（我们称之为二体问题），只考虑地球质心引力作用下的卫星轨道称为无摄轨道，同时考虑各种摄动力作用下的轨道称为受摄轨道。对于二体问题，根据牛顿第二定律，卫星的运动方程就可以写作
r
¨
=
−
G
(
M
+
m
)
r
3
r
\ddot{r} = -\frac{G(M+m)}{r^3}r
r¨=−r3G(M+m)r
其中， M 为地球的质量， m 为卫星的质量（在很多情况下，卫星的质量是未知的，并且相对于地球而言，卫星的质量太小，所以一般不予考虑），
r
{r}
r为卫星在地心惯性坐标系中的位置向量，
r
¨
\ddot{r}
r¨ 为卫星在地心惯性坐标系中的加速度向量。
因为上面卫星的运动方程是二阶常系数微分方程，所以需要6个积分常数（三维，两次积分），轨道根数就是用来确定积分常数的，所以是六个。
3. 2 开普勒方程
c
o
s
E
=
e
+
c
o
s
θ
1
+
e
c
o
s
θ
cosE=\frac{e+cosθ}{1+e cosθ}
cosE=1+ecosθe+cosθ
s
i
n
E
=
1
−
e
2
s
i
n
θ
1
+
e
c
o
s
θ
sinE= \frac{\sqrt{1-e^2} sinθ}{1+e cosθ}
sinE=1+ecosθ1−e2sinθ
E
=
2
t
a
n
−
1
(
1
−
e
1
+
e
t
a
n
(
θ
2
)
)
E = 2tan^-1(\sqrt{\frac{1-e}{1+e}}tan(\frac{θ}{2}))
E=2tan−1(1+e1−etan(2θ))
则开普勒方程为
M
=
E
−
E
s
i
n
E
M=E-EsinE
M=E−EsinE
3. 3 计算卫星在轨道中位置
3. 4 轨道坐标系与大地坐标系转换
补充：欧拉角、旋转向量和旋转矩阵的相互转换
欧拉角转为旋转矩阵的公式如下：
未完待续…
参考链接：
轨道六根数
开普勒轨道参数
卫星轨道推演计算相关知识点总结
卫星运动基本知识
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
