针对抠图的评价指标

1. SAD - 绝对误差和（Sum of absolute difference）

$$SAD=\sum _i|{\alpha }_i-{\alpha }_i^{\ast }|$$
其中，$\alpha$ 为 predicted matte，${\alpha }_i^{\ast }$ 为 groundtruth matte。

def matte_sad(pred_matte, gt_matte):
    assert (len(pred_matte.shape) == len(gt_matte.shape))
    error_sad = np.sum(np.abs(pred_matte - gt_matte))    
    return error_sad

2. MAD - 平均绝对差值（Mean absolute difference）

$$MAD=\frac{1}{n}\sum _{i=1}^n|{\alpha }_i-{\alpha }_i^{\ast }|$$
其中，$\alpha$ 为 predicted matte，${\alpha }_i^{\ast }$ 为 groundtruth matte。MAD 与 SAD 类似，二者选其一即可。

def matte_mad(pred_matte, gt_matte):
    assert (len(pred_matte.shape) == len(gt_matte.shape))
    error_mad = np.mean(np.abs(pred_matte - gt_matte))    
    return error_mad

3. MSE - 均方误差（Mean squared error）

$$MSE=\frac{1}{n}\sum _{i=1}^n({\alpha }_i-{\alpha }_i^{\ast }{)}^2$$
其中，$\alpha$ 为 predicted matte，${\alpha }_i^{\ast }$ 为 groundtruth matte。

def matte_mse(pred_matte, gt_matte):
    assert (len(pred_matte.shape) == len(gt_matte.shape))
    error_mse = np.mean(np.power(pred_matte - gt_matte, 2))    
    return error_mse

4. Gradient error

$$Grd\_error=\sum ({\nabla }_{{\alpha }_i}-{\nabla }_{{\alpha }_i^{\ast }}{)}^2$$
其中，${\nabla }_{{\alpha }_i}$ 和 ${\nabla }_{{\alpha }_i^{\ast }}$ 表示对应alpha matte的归一化梯度, 是通过将matte与具有方差sigma的一阶Gaussian导数滤波器进行卷积计算得到的。计算二者差异, 进而累计损失。总体越相似,gradient error越小。

def matte_grad(pred_matte, gt_matte):
    assert(len(pred_matte.shape) == len(gt_matte.shape))
    # alpha matte 的归一化梯度，标准差 =1.4，1 阶高斯导数的卷积
    predict_grad = scipy.ndimage.filters.gaussian_filter(pred_matte, 1.4, order=1) 
    gt_grad = scipy.ndimage.filters.gaussian_filter(gt_matte, 1.4, order=1)
    error_grad = np.sum(np.power(predict_grad - gt_grad, 2))
    return error_grad

5. Connectivity error

$$Conec\_error=\sum _i(\phi ({\alpha }_i,\Omega )-\phi ({\alpha }_i^{\ast },\Omega ))$$
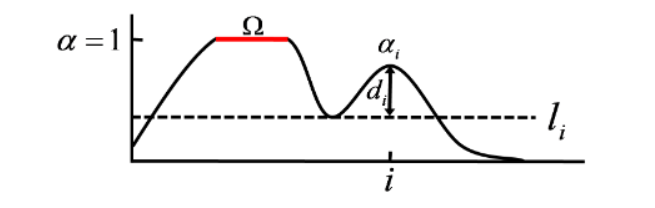
上式给出了连通性误差的计算方法, 是对整个预测出来的alpha matte图和相应的Ground truth的对应的差异的累和。关键在于 $\phi ({\alpha }_i,\Omega )$ 函数，源域 $\Omega$ 由最大连通域定义，最大连通域是指alpha matte和它对应的Ground truth都完全不透明的部分（即 $\alpha$ 都为 1），如上图红线区域大致表示。

  连接程度由距离 $d_i$ 决定, $d_i={\alpha }_i-l_i$，其中 $l_i$ 是像素 $i$ 能四连通到 $\Omega$ 的最大阈值，也就是上图中的虚线，阈值大于这个，像素 $i$ 就与 $\Omega$ 不连通了。 用 它 对alpha matte进行二值化，正好处于使像素 $i$ 与源域连通（实 际 需 要 四 连 通 ) / 不 连 通 的 临 界 . 若 是 对 于 一 个 像 素 而 言 , 它 的 不连通了。用它对alpha matte进行二值化, 正好处于使像素i与源域连通(实际需要四连通)/不连通的临界. 若是对于一个像素而言, 它的不连通了。用它对‘alphamatte‘进行二值化,正好处于使像素i与源域连通(实际需要四连通)/不连通的临界。若是对于一个像素而言，它的 $l_i={\alpha }_i$，那么就可以认为它与源域是全连通的。$i$ 点连通度 $\alpha$ 的定义如下：
$$\phi ({\alpha }_i,\Omega )=1-({\lambda }_i\cdot \delta (d_i\ge \theta )\cdot d_i)$$
其中， $\theta$ 为自定义参数，它用在指示函数 $\delta$ 里作为一个阈值, 用以忽略小于它的 $d_i$ 的情况, 认为小于它就已经是全连通了, 使得误差计算更为灵活。${\lambda }_i=\frac{1}{k}{\sum }_{k\in K}dis{t}_k(i)$ 用来对 $d_i$ 进行加权, 这里的 $K$ 表示 $l_i$ 到 ${\alpha }_i$ 间的离散 $\alpha$ 值的集合，$dis{t}_k$计算了设置为阈值 $k$ 时, 对于像素 $i$ 距离最近的连通到源域的像素，与像素 $i$ 之间的标准化欧式距离。实际情况中，远离连通区域的像素，获得的权重 $\lambda$ 也应该相应会更大些，这样导致得到的 $\phi$ 会更小些，也就是认为连通度更小。
  按公式定义的 $\lambda$ 的计算量太大，在实际应用中计算开销太大，为减小计算可把 ${\lambda }_i$ 直接取为 1。

【转载自】Image Matting 客观评价指标、数据集及主观评价；