LightOJ 1151 Snakes and Ladders(期望dp+高斯消元)

Snakes and Ladders

‘Snakes and Ladders’ or ‘Shap-Ludu’ is a game commonly played in Bangladesh. The game is so common that it would be tough to find a person who hasn’t played it. But those who haven’t played it (unlucky of course!) the rules are as follows.

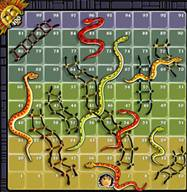
1.There is a 10 x 10 board containing some cells numbered from 1 to 100.
2.You start at position 1.
3.Each time you throw a perfect dice containing numbers 1 to 6.
4.There are some snakes and some ladders in the board. Ladders will take you up from one cell to another. Snakes will take you down.
5.If you reach a cell that contains the bottom part of a ladder, you will immediately move to the cell which contains the upper side of that ladder. Similarly if you reach a cell that has a snake-head you immediately go down to the cell where the tail of that snake ends.
6.The board is designed so that from any cell you can jump at most once. (For example there is a snake from 62 to 19, assume that another is from 19 to 2. So, if you reach 62, you will first jump to 19, you will jump to 2. These kinds of cases will not be given)
7.There is no snake head in the 100-th cell and no ladder (bottom part) in the first cell.
8.If you reach cell 100, the game ends. But if you have to go outside the board in any time your move will be lost. That means you will not take that move and you have to throw the dice again.
Now given a board, you have to find the expected number of times you need to throw the dice to win the game. The cases will be given such that a result will be found.

Input
Input starts with an integer T (≤ 105), denoting the number of test cases.

The first line of a case is a blank line. The next line gives you an integer n denoting the number of snakes and ladders. Each of the next n lines contain two integers a and b (1 ≤ a, b ≤ 100, a ≠ b). If a < b, it means that there is a ladder which takes you from a to b. If a > b, it means that there is a snake which takes you from a to b. Assume that the given board follows the above restrictions.

Output
For each case of input, print the case number and the expected number of times you need to throw the dice. Errors less than $10^{-6}$ will be ignored.

Sample Input

2

14
4 42
9 30
16 8
14 77
32 12
37 58
47 26
48 73
62 19
70 89
71 67
80 98
87 24
96 76

0

Sample Output

Case 1: 31.54880806
Case 2: 33.0476190476

题意
从1走到100，每次走的步数投骰子决定1-6步，但是路上有些点是单向传送的，即只能从这个点传到给定点，并且不会出现首尾相连的情况。问走到100的投骰子次数的期望。

题解
第一眼是期望DP，但是存在传送点，且传送是可能往前可能往后的，所以递推是无法解决的。看看了网上的题解，才知道列成方程由高斯消元解出答案。
首先确认传送是怎样传送的，是从$i$传送到$tp[i]$
错的思路：
然后就是没有传送的情况：$dp[i]=1+\frac{1}{min(6,n-i)}\sum _{j=1}^{min(6,n-i)}dp[i+j]$
传送的情况：$dp[i]=dp[tp[i]]$
没有传送的稍稍化简一下：
令$k=min(6,n-i)$
有$$\begin{array}{rl}dp[i]& =1+\frac{1}{k}\sum _{j=1}^{k}dp[i+j]\\ k\cdot dp[i]& =k+\sum _{j=1}^{k}dp[i+j]\\ k\cdot dp[i]-\sum _{j=1}^{k}dp[i+j]& =k\end{array}$$
又有传送的：$$dp[i]-dp[tp[i]]=0$$
对的思路：
不传送部分：$$\begin{array}{rl}dp[i]& =\frac{1}{6}\sum _{j=1}^{k}dp[i+j]+\frac{1}{6}\sum _{j=k+1}^{6}dp[i]+1\\ k\cdot dp[i]-\sum _{j=1}^{k}dp[i+j]& =6\end{array}$$

代码

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const int MOD = 998244353;

const int maxn=105;
const double eps=1e-8;
double a[maxn][maxn];

double x[maxn];//解集
bool free_x[maxn];
int n;
 
int sgn(double x)
{
    return (x>eps)-(x<-eps);
}
// 高斯消元法解方程组(Gauss-Jordan elimination).(0表示无解，1表示唯一解，大于1表示无穷解，并返回自由变元的个数)
int Gauss(int equ,int var)
{
    //equ个方程,var个变量
    //equ=n,var=n;//多少个方程，多少个变量
    int i,j,k;
    int max_r; // 当前这列绝对值最大的行.
    int col; // 当前处理的列.
    double temp;
    int free_x_num;
    int free_index;
    // 转换为阶梯阵.
    col=0; // 当前处理的列.
    memset(free_x,true,sizeof(free_x));
    for(k=0;k<equ&&col<var;k++,col++){
        max_r=k;
        for(i=k+1;i<equ;i++){
            if(sgn(fabs(a[i][col])-fabs(a[max_r][col]))>0)
                max_r=i;
        }
        if(max_r!=k){ // 与第k行交换.
            for(j=k;j<var+1;j++)
                swap(a[k][j],a[max_r][j]);
        }
        if(sgn(a[k][col])==0){ // 说明该col列第k行以下全是0了，则处理当前行的下一列.
            k--; continue;
        }
        for(i=k+1;i<equ;i++){ // 枚举要删去的行.
            if (sgn(a[i][col])!=0){
                temp=a[i][col]/a[k][col];
                for(j=col;j<var+1;j++){
                    a[i][j]=a[i][j]-a[k][j]*temp;
                }
            }
        }
    }
 
    for(i=k;i<equ;i++){
        if (sgn(a[i][var])!=0)
            return 0;
    }
    if(k<var){
        for(i=k-1;i>=0;i--){
            free_x_num=0;
            for(j=0;j<var;j++){
                if (sgn(a[i][j])!=0&&free_x[j])
                    free_x_num++,free_index=j;
            }
            if(free_x_num>1) continue;
            temp=a[i][var];
            for(j=0;j<var;j++){
                if(sgn(a[i][j])!=0&&j!=free_index)
                    temp-=a[i][j]*x[j];
            }
            x[free_index]=temp/a[i][free_index];
            free_x[free_index]=0;
        }
        return var-k;
    }
 
    for (i=var-1;i>=0;i--){
        temp=a[i][var];
        for(j=i+1;j<var;j++){
            if(sgn(a[i][j])!=0)
                temp-=a[i][j]*x[j];
        }
        x[i]=temp/a[i][i];
    }
    return 1;
}
int tp[maxn];
int main(){
    int t,ca=1;cin>>t;
    while(t--){
        int n;scanf("%d",&n);
        memset(a,0,sizeof a);
        memset(tp,0,sizeof tp);
        memset(x,0,sizeof x);
        for(int i = 1; i <= n; ++i){   
            int p,pp;
            scanf("%d%d",&p,&pp);
            tp[p]=pp;
        }
        
        for(int i = 1; i <= 99; ++i){  
            if(tp[i]){
                a[i][i]=1;a[i][tp[i]]=-1;a[i][101]=0;
            }
            else{
                int k=min(6,100-i);
                a[i][i]=k;
                for(int j = 1; j <= k; ++j){
                    a[i][i+j]=-1;
                }
                a[i][101]=6;
            }
            
        }
        a[100][100]=1;
        Gauss(105,101);
        printf("Case %d: %.10f\n",ca++,x[1]);
    }
}