数值分析(5)：插值法

1. 引言

本章探讨的是如果有n个点$(x_i,f(x_i))$，如何找到一个函数$\phi (x)$去拟合$f(x)$，也就是精确地穿过这n个点。

$f(x)$称为被插值函数，$\phi (x)$称为插值函数，$x_i$称为插值节点$(i=0,1,\dots ,n)$，$\phi (x_i)=f(x_i)$称为插值条件,$[a,b]$称为插值区间，$R(x)=f(x)一p(x)$称为插值余项。

用代数多项式作为插值函数的插值法称为多项式插值，相应的多项式称为插值多项式。

本章会用到的几个重要定理为：

1. 代数基本定理告诉我们：n次多项式最多有n个不同零点(n ≥ 1)。那么不超过n次的多项式在(n+1）个不同点取值相同有什么结论？答案是：这是个常值多项式。

2. 首先来看函数族的线性相关性的定义
   
   可以证明：
   
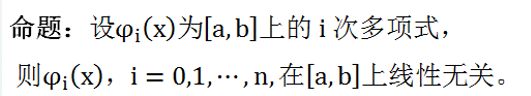
   也就是它们是相互正交的“基”，这一点从泰勒展开也可以知道。

3. 多项式插值的存在唯一性
   这一点其实是显然的，n个方程n个未知数，且系数矩阵必定可逆，证明如下：
   

2. lagrange插值

拉格朗日插值的思路很简单，就是设计 基函数$l(x)$ 使得$L_n(x)$能够拟合$f(x)$，如下式所示：

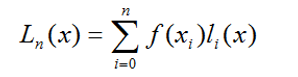
$l_i(x)$的特点是，当$x=x_i$时，$l_i(x_i)=1$，当$x=x_j\ne x_i$时，$l_i(x_j)=0$，这样一来，$L_n(x)$就能穿过n+1个$(x_i,f(x_i))$。$L_n(x)$称为n次Lagrange插值多项式，$l_i(x)$又称作n次插值基函数，$x_i(i=0,1,...,n)$称为插值节点。

而对于这样的$l_i(x)$如何构造？可以使用如下方法：

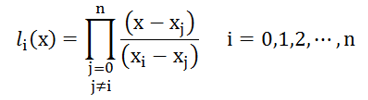
可以看到分子分母都只有$n$项。注意n次Langrange插值多项式$L_n(x)$穿过的是$n+1$个点。

显然，Lagrange插值基函数具有以下三个性质：

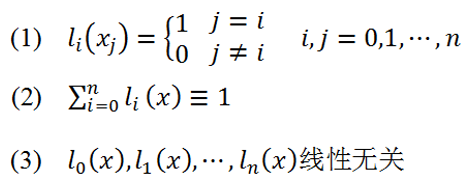
毫无疑问，Langrange插值多项式在给定的$n+1$个点上与$f(x)$相比是毫无误差的，那么进一步地，我想知道不在这给定的$n+1$个点上，$L_n(x)$和$f(x)$之间的差异，这就需要用到插值余项的概念。

即令插值多项式余项或称插值余项$R_n(x)$为：
$$R_n(x)=f(x)-L_n(x)$$

对于lagrange插值多项式，插值余项为：

进一步地有一个推论：

3. Newton插值

lagrange插值的弊端是，根据n+1个$(x_i,f(x_i)),i=0,1,...,n$能够插出$L_n(x)$，但是如果突然增加一个点$(x_{n+1},f(x_{n+1}))$，所得到的$L_{n+1}(x)$与$L_n(x)$相差极大，所有的插值基函数都要重新计算一遍。

而Newton插值法就是为了解决这个问题，使得每增加一个新点，插值多项式只需要在末尾增加一项即可，前面的不变，具有“继承”的特性。

首先来介绍均差的概念：

可以看到均差左边中括号内的字母集是右边中括号内的两个字母集的并集，且右边中括号内的两个字母集各有一个独有的字母，分母就是这两个独有字母之差。用这种方式能够很快地记住均差的公式。

关于均差有如下三条性质：

那么具体在计算这些n阶均差时，有没有简单的方法呢？下面介绍两种方法：

1. 用定义，列均差表
   
   可以看到用均差表的计算方法是：首先找到要计算的均差值，以它为顶点画一个三角形，然后顶点左边的两列相减除以三角形最左边对应的变量之差。

2. 用均差性质做计算，如下题用第三条性质求导后能够直接得到结果。
   

有了均差的概念以后，就可以得到Newton插值多项式：

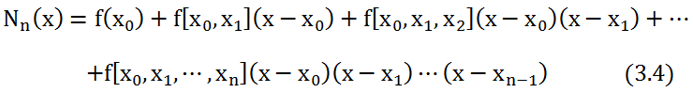
同样地，在$n+1$个插值点$x_i$处，$N_n(x_i)=f(x_i)$，但是对于不在插值点处的$x$，那么$N_n(x)$与$f(x)$的相差是多少呢？这同样需要用到插值余项的概念，Newton插值余项$R_n(x)$的定义与lagrange插值余项定义相同，为：
$$R_n(x)=f(x)-N_n(x)$$

通过均差性质可以计算得：

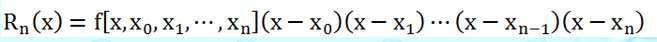
可以看到Newton插值余项的形式更加简洁，不存在导数，且能够被准确地确定下来。而lagrange插值余项中存在的$\xi$是无法得知的，因此lagrange插值余项无法被准确地确定下来。Newton的这种插值余项称为均差型余项。

同样，Newton插值余项也可以用微分的形式来表示，即：

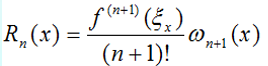
上面的形式称为微分型余项。而微分型余项与均差型余项的关系就是均值的第三条性质。

4. Hermite插值

Hermite插值是带导数的插值，即对于被插值函数$f(x)$，不仅给了$x_i$的函数值$f(x_i)$，还给了导数值$f^{\prime }(x_i)$，那么此时如何确定插值函数$\phi (x)$？

此时的插值函数用$H(x)$记号表示，Hermite插值多项式的定义如下：

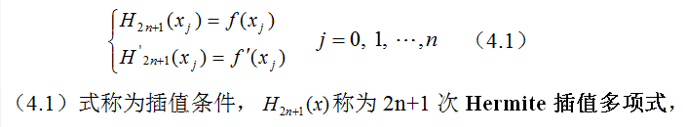
求解Hermite插值多项式的方法有以下三个：

1.待定系数法

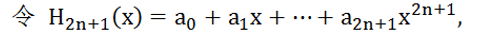
即用$2n+2$个方程，求解$2n+2$个变量，需要求一次导。

2.基函数法（类似于Lagrange插值法）

如上所示：

${\alpha }_j(x)$是一个$2n+1$次的多项式，它的作用是，当$x=x_j$时，${\alpha }_j(x_j)=1$；当$x=x_i\ne x_j$时，${\alpha }_j(x_i)=0$；而求导后的${\alpha }_j^{\prime }(x)$，无论$x$是否为$x_j$，都等于0（注意只是$n+1$个点的导数，不是所有点的导数）

${\beta }_j(x)$是一个$2n+1$次的多项式，它的作用是，无论$x$是否为$x_j$，${\beta }_j(x)$都等于0（注意只是$n+1$个点，不是所有点）。当$x=x_j$时，${\beta }_j^{\prime }(x_j)=1$；当$x=x_i\ne x_j$时，${\beta }_j^{\prime }(x_i)=0$

而满足上述条件的${\alpha }_j(x),{\beta }_j(x)$为：

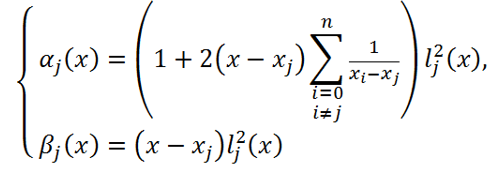
这种基函数的插值余项$R_{2n+1}(x)$为：

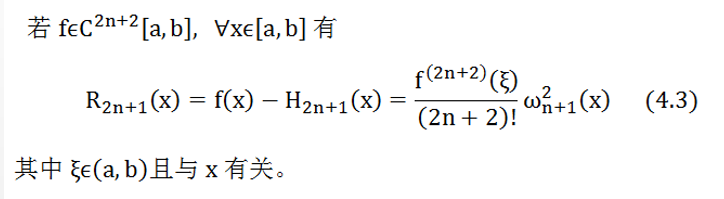
3.类似于Newton插值的插值多项式

在此之前，首先来回顾一下，如果有$2n+2$个相异节点$(x_i,f(x_i))$，那么得到的Newton多项式为：

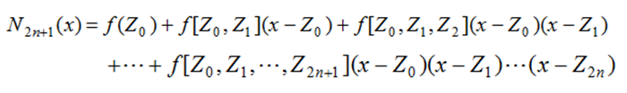
但此时，给定的函数值节点$(x_i,f(x_i))$只有$n+1$个，还有$n+1$个导数值节点$(x_i,f^{\prime }(x_i))$。那么我们可以理解为存在$2n+2$个点，只不过总是有两个自变量取值相同的点（或者说无限地靠近），那么相异节点其实只有$n+1$个，那么此时插值多项式为：

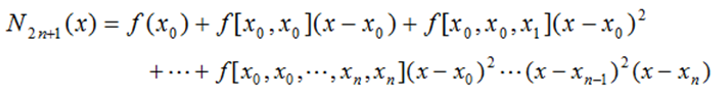
上式就是 Hermite插值多项式第三个方法

当然，上述方法需要用到以下两个概念，一个是重节点均差，一个是均差的导数。

在说明这两个概念之前，首先来看一个重要的引理：

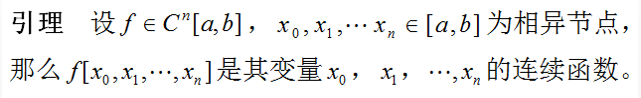
重节点均差的概念如下：

均差的导数的概念如下：

那么这种插值方法的插值余项$R_{2n+1}(x)$，既可以和第二种lagrange插值方式一样，写成：

也可以写成：

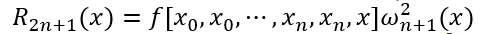
当然，这种插值方式因为需要用到均差的概念，所以也可以列出均差表，而这个均差表有需要注意的地方，就是存在导数的自变量需要写两遍，并且在第二遍的一阶均差位置处写上导数值，如下例所示：

参考文献：

关治，陆金甫《数值方法》