EGO-Planner An ESDF-Free Gradient-Based Local Plan for Quadrotors

EGO-Planner: An ESDF-Free Gradient-Based Local Planner for Quadrotors

EGO-Planner: An ESDF-free Gradient-based Local Planner for Quadrotors

https://github.com/ZJU-FAST-Lab/ego-planner

摘要

• 欧氏符号距离场（Euclidean Signed Distance Field，ESDF）常用于估计梯度大小和方向
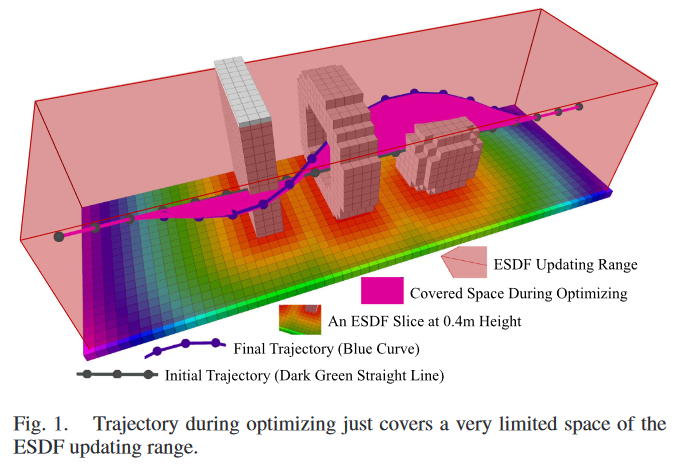
• 轨迹规划只在ESDF很小的子空间进行，更新整个ESDF不必要
• 本文提出ESDF-free的基于梯度的规划框架
• 罚函数的碰撞项基于对比有碰撞的轨迹和无碰撞的引导路径，只有轨迹碰撞新的障碍物时规划器才提取必要的障碍物信息
• 若轨迹是动力学不可行的，则延长轨迹的时间

引言

构建ESDF的方式有两种：

• 增量式全局更新（incremental global updating）
• 批量式局部计算（batch local calculation）

二者都没有考虑轨迹本身，不能单独直地接服务于轨迹优化

本文提出了ESDF-free基于梯度的局部规划框架（ESDF-free Gradient-based lOcal planning framework，EGO），包含

• 基于梯度的样条优化器
  • 对比轨迹和无碰撞的引导路径
  • 在有碰撞的轨迹上施加力并生成估计的梯度以使轨迹远离障碍物
  • 轨迹会在附近的障碍物之间反弹几次，并稳定在安全区域内
  • 只计算必要的梯度，避免计算和局部轨迹无关的梯度
• 随后的改进过程
  • 若轨迹不符合动力学约束，则进入改进过程
  • 给轨迹分配更长的时间，产生新的B样条
  • 新轨迹拟合之前的轨迹，在轴向和径向（axial and radial directions）上使用不同的惩罚，以增强鲁棒性

主要贡献：

• 提出新的基于梯度的四旋翼无人机局的部规划方法，其直接从障碍物评估和投影梯度信息
• 提出轻量级的轨迹改进方法，使用各向异性（anisotropic）误差惩罚生成更平滑的轨迹
• 把上述方法集成到四旋翼无人机系统中并开源了软件

相关工作

主要分为两部分：

• 基于梯度的运动规划
  • 把局部轨迹生成建模为无约束的非线性优化问题
  • 常依赖ESDF
• 欧式符号距离场ESDF
  • 常用于从带噪声的传感器参数中构造物体
  • 常包含冗余信息

避碰力估计

优化变量为控制点$\mathbf{Q}$，每个控制点独立拥有自己的环境信息

1. 不考虑碰撞，给出满足初末状态约束的B样条曲线$\Phi$
2. 一次迭代中检测到的每一个碰撞，生成一条无碰撞轨迹$\Gamma$
3. 碰撞段的每个控制点${\mathbf{Q}}_i$在障碍物表面分配一个锚点${\mathbf{p}}_{ij}$和相应的排斥力方向${\mathbf{v}}_{ij}$
4. 省略了下表的每个 { p , v } \{\mathbf{p}, \mathbf{v}\} {p,v}对只对应一个特定的控制点，其生成过程如算法1和图3所示
5. 从${\mathbf{Q}}_i$到第j个障碍物的距离定义为

$$d_{ij}=\left({\mathbf{Q}}_i-{\mathbf{p}}_{ij}\right)\cdot {\mathbf{v}}_{ij}$$

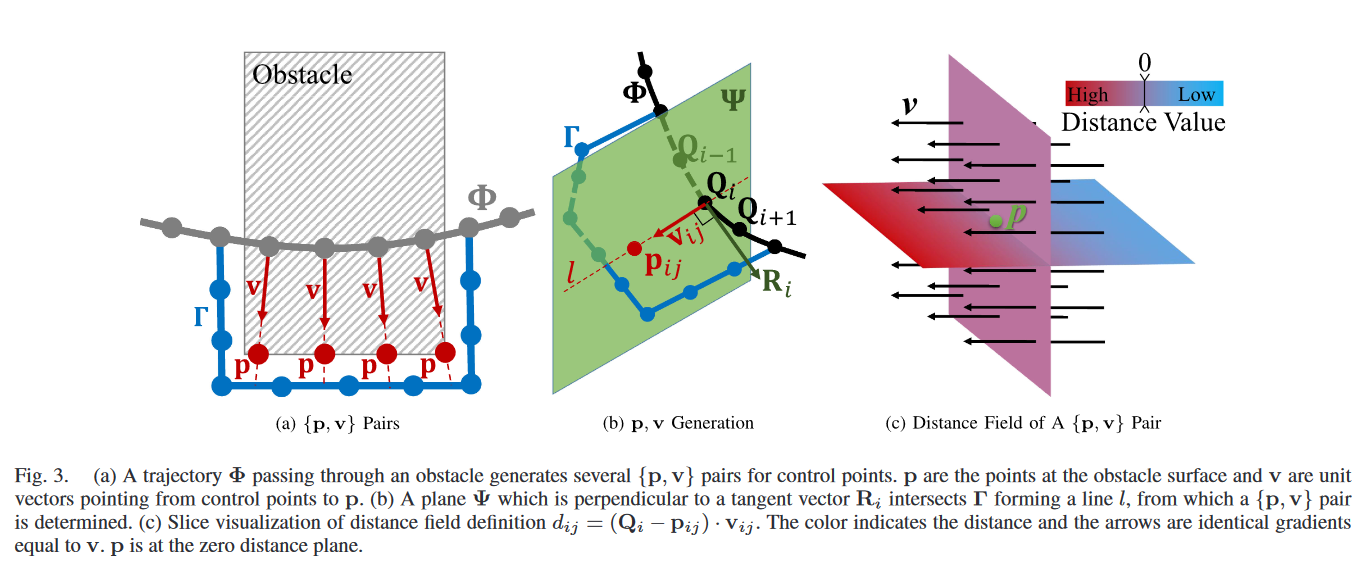
• 为了避免轨迹离开障碍物前重复生成 { p , v } \{\mathbf{p}, \mathbf{v}\} {p,v}对，本文认为只有对所有 $j$满足 $d_{ij}>0$时${\mathbf{Q}}_i$原本所在的障碍物是才是新发现的
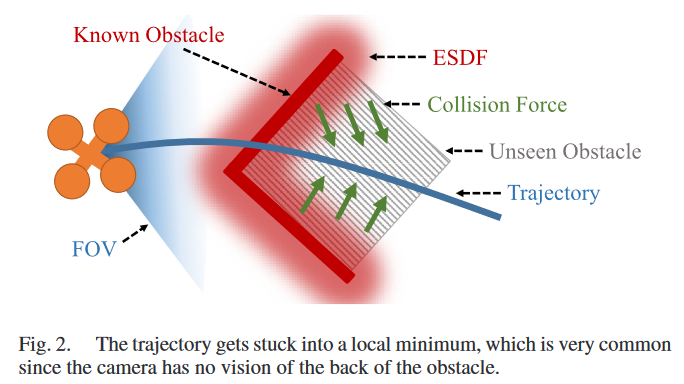
• 基于ESDF的规划器容易陷入如下图的局部最优而无法避碰，故需要无碰撞的初始轨迹

基于梯度的轨迹优化

问题定义

轨迹建模为均匀B样条曲线$\Phi$，其次数为$p_b$，$N_c$个控制点为 { Q 1 , Q 2 , … , Q N c } \left\{\mathbf{Q}_1, \mathbf{Q}_2, \ldots, \mathbf{Q}_{N_c}\right\} {Q1​,Q2​,…,QNc​​}，节点向量为 { t 1 , t 2 , … , t M } \left\{t_1, t_2, \ldots, t_M\right\} {t1​,t2​,…,tM​}，且满足$M=N_c+p_b$（B样条固有的性质）。

由于是均匀B样条，故节点区间$\Delta t=t_{m+1}-t_m$相等，则速度、加速度和加加速度可表示为

$${\mathbf{V}}_i=\frac{{\mathbf{Q}}_{i+1}-{\mathbf{Q}}_i}{\Delta t},{\mathbf{A}}_i=\frac{{\mathbf{V}}_{i+1}-{\mathbf{V}}_i}{\Delta t},{\mathbf{J}}_i=\frac{{\mathbf{A}}_{i+1}-{\mathbf{A}}_i}{\Delta t}$$

优化问题表示为

$$\underset{\mathbf{Q}}{\min }J={\lambda }_s{J}_s+{\lambda }_c{J}_c+{\lambda }_d{J}_d$$

其中等是右侧三项依次表示平滑性惩罚、碰撞惩罚和可行性惩罚

平滑性惩罚

只取轨迹的几何信息，在没有时间积分的情况下惩罚加速度和加加速度的平方

$$J_s=\sum _{i=1}^{N_c-1}{\Vert {\mathbf{A}}_i\Vert }_2^2+\sum _{i=1}^{N_c-2}{\Vert {\mathbf{J}}_i\Vert }_2^2$$

碰撞惩罚

定义安全距离$s_f$并惩罚$d_{ij}<s_f$的控制点，本文设计了二次连续可微的罚函数$j_c$并在$d_{ij}$减小时减小其斜率

$$\begin{array}{rl}{j}_c(i,j)& =\{\begin{array}{ll}0& \left(c_{ij}\le 0\right)\\ c_{ij}^3& \left(0<c_{ij}\le s_f\right)\\ 3s_f{c}_{ij}^2-3s_f^2{c}_{ij}+s_f^3& \left(c_{ij}>s_f\right)\end{array}\\ c_{ij}& =s_f-d_{ij},\end{array}$$

其中$j_c(i,j)$源于${\mathbf{Q}}_i$上的 { p , v } j \{\mathbf{p}, \mathbf{v}\}_j {p,v}j​对

• 每个${\mathbf{Q}}_i$的成本独立评估，故发现更多障碍物的控制点有更高的轨迹形变权重
• 第$i$个控制点的成本增加值为$j_c\left({\mathbf{Q}}_i\right)={\sum }_{j=1}^{N_p}{j}_c(i,j)$，其中$N_p$为${\mathbf{Q}}_i$的 { p , v } j \{\mathbf{p}, \mathbf{v}\}_j {p,v}j​对数量

总成本为

$$J_c=\sum _{i=1}^{N_c}{j}_c\left({\mathbf{Q}}_i\right)$$

总成本关于${\mathbf{Q}}_i$的导数为

$$\frac{\partial J_c}{\partial {\mathbf{Q}}_i}=\sum _{i=1}^{N_c}\sum _{j=1}^{N_p}{\mathbf{v}}_{ij}\{\begin{array}{lr}0& \left(c_{ij}\le 0\right)\\ -3c_{ij}^2& \left(0<c_{ij}\le s_f\right)\\ -6s_f{c}_{ij}+3s_f^2& \left(c_{ij}>s_f\right)\end{array}$$

可行性惩罚

限制轨迹的高阶导数$\left|{\Phi }_r^{(k)}(t)\right|<{\Phi }_{r,\max }^{(k)}$，其中 r ∈ { x , y , z } r \in\{x, y, z\} r∈{x,y,z}表示每个维度

罚函数的表达式为

$$J_d=\sum _{i=1}^{N_c}{w}_{v}F\left({\mathbf{V}}_i\right)+\sum _{i=1}^{N_c-1}{w}_{a}F\left({\mathbf{A}}_i\right)+\sum _{i=1}^{N_c-2}{w}_{j}F\left({\mathbf{J}}_i\right)$$

其中各项函数

$$F(\mathbf{C})=\sum _{r=x,y,z}f\left(c_r\right)$$

$$f\left(c_r\right)=\{\begin{array}{lr}{a}_1{c}_r^2+b_1{c}_r+c_1& \left(c_r\le -c_j\right)\\ {\left(-\lambda c_m-c_r\right)}^3& \left(-c_j<c_r<-\lambda c_m\right)\\ 0& \left(-\lambda c_m\le c_r\le \lambda c_m\right)\\ {\left(c_r-\lambda c_m\right)}^3& \left(\lambda c_m<c_r<c_j\right)\\ a_2{c}_r^2+b_2{c}_r+c_2& \left(c_r\ge c_j\right)\end{array}$$

其中 c r ∈ C ∈ { V i , A i , J i } c_r \in \mathbf{C} \in\left\{\mathbf{V}_i, \mathbf{A}_i, \mathbf{J}_i\right\} cr​∈C∈{Vi​,Ai​,Ji​}

数值求解

上述定义的问题有如下特点：

• 目标函数根据新发现的障碍物自适应变化
• 目标函数近似二次函数

采用梯度信息近似逆Hessian矩阵的拟牛顿法求解

L-BFGS算法平衡了重启损失（loss of restart）和逆Hessian矩阵的估计精度，该算法求解无约束优化问题

$$\underset{\mathbf{x}\in {\mathbb{R}}^n}{\min }f(\mathbf{x})$$

每步更新为

$${\mathbf{x}}_{k+1}={\mathbf{x}}_k-{\alpha }_k{\mathbf{H}}_k\nabla {\mathbf{f}}_k$$

$${\mathbf{H}}_{k+1}={\mathbf{V}}_k^T{\mathbf{H}}_k{\mathbf{V}}_k+{\rho }_k{\mathbf{s}}_k{\mathbf{s}}_k^T$$

其中${\rho }_k={\left({\mathbf{y}}_k^T{\mathbf{s}}_k\right)}^{-1},{\mathbf{V}}_k=\mathbf{I}-{\rho }_k{\mathbf{y}}_k{\mathbf{s}}_k^T,{\mathbf{s}}_k={\mathbf{x}}_{k+1}-{\mathbf{x}}_k,{\mathbf{y}}_k=\nabla {\mathbf{f}}_{k+1}-\nabla {\mathbf{f}}_k$

此处不精确计算${\mathbf{H}}_k$，更新过程满足双循环更新方法，具有线性的时间和空间复杂度。Barzilai-Borwein步的权重作为初始逆Hessian矩阵${\mathbf{H}}_k^0$

Barzilai-Borwein (BB) method也是梯度下降方法的一种，他主要是通过近似牛顿方法来实现更快的收敛速度，同时避免计算二阶导数带来的计算复杂度。

$${\mathbf{H}}_k^0=\frac{{\mathbf{s}}_{k-1}^T{\mathbf{y}}_{k-1}}{{\mathbf{y}}_{k-1}^T{\mathbf{y}}_{k-1}}\mathbf{I}\text{ or }\frac{{\mathbf{s}}_{k-1}^T{\mathbf{s}}_{k-1}}{{\mathbf{s}}_{k-1}^T{\mathbf{y}}_{k-1}}\mathbf{I}$$

时间重分配和轨迹改进

本节主要解决轨迹不可行的问题

首先计算超出极限值的比例

$$r_e=\max \left\{\left|{\mathbf{V}}_{i,r}/v_m\right|,\sqrt{\left|{\mathbf{A}}_{j,r}/a_m\right|},\sqrt[3]{\left|{\mathbf{J}}_{k,r}/j_m\right|},1\right\}$$

之后重新计算新均匀B样条轨迹${\Phi }_f$的节点区间

$$\Delta t^{\prime }=r_e\Delta t$$

新轨迹${\Phi }_f$要保持和原轨迹${\Phi }_s$相同的形状和控制点数量，由光滑性、可行性和曲线拟合组成的罚函数为

$$\underset{\mathbf{Q}}{\min }{J}^{\prime }={\lambda }_s{J}_s+{\lambda }_d{J}_d+{\lambda }_f{J}_f$$

由于拟合后的曲线已经无碰撞，故设计：

• 低惩罚权重的轴向位移以放松平滑性调节限制
• 高惩罚权重的径向位移以避免碰撞

为了实现这一点，本文采用下图所示的椭球度量

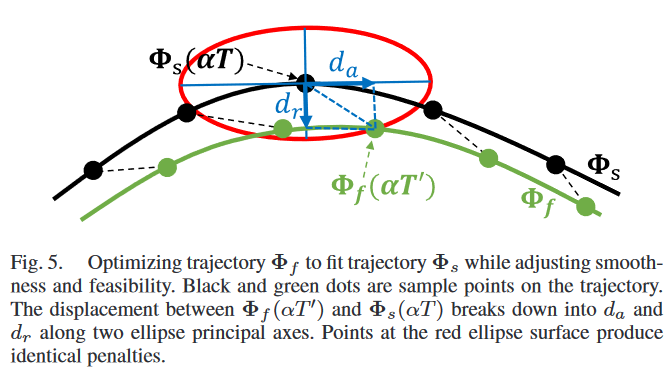
则轴向位移$d_a$和径向位移$d_r$为

$$\begin{array}{rl}& d_a=\left({\mathbf{\Phi }}_f-{\mathbf{\Phi }}_s\right)\cdot \frac{{\dot{\mathbf{\Phi }}}_s}{\Vert {\dot{\mathbf{\Phi }}}_s\Vert },\\ & d_r=\Vert \left({\mathbf{\Phi }}_f-{\mathbf{\Phi }}_s\right)\times \frac{{\dot{\mathbf{\Phi }}}_s}{\Vert {\dot{\mathbf{\Phi }}}_s\Vert }\Vert \end{array}$$

则拟合惩罚为

$$J_f={\int }_0^1\left[\frac{d_a{\left(\alpha T^{\prime }\right)}^2}{a^2}+\frac{d_r{\left(\alpha T^{\prime }\right)}^2}{b^2}\right]\mathrm{d}\alpha$$

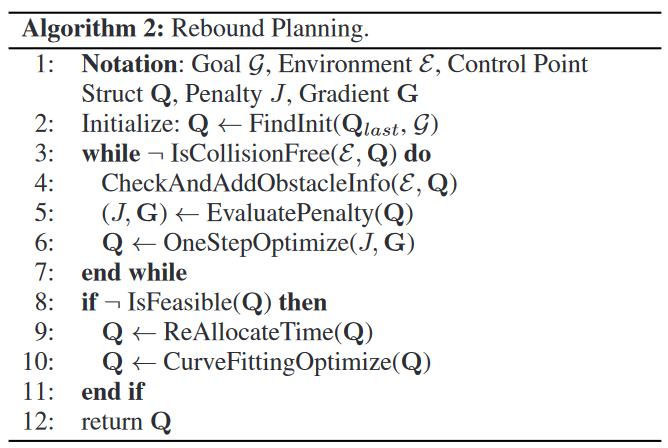
后面没细看了，整个框架流程如下图算法2