卡尔曼滤波器简介——α−β−γ滤波器

无损检测小白白

已于 2023-04-27 18:50:04 修改

阅读量1.8k

点赞数 3

分类专栏：雷达基础知识文章标签：算法

于 2023-04-27 18:41:58 首次发布

本文链接：https://blog.csdn.net/qq_42046837/article/details/130395840

版权

雷达基础知识专栏收录该内容

17 篇文章 21 订阅

订阅专栏

原文：The alpha - beta - gamma filter (kalmanfilter.net)

本章是介绍性的，它描述了α−β和α−β−γ滤波器。这些滤波器经常用于时间序列数据平滑。α−β-(γ)滤波的原则与卡尔曼滤波原理密切相关。

示例 1 – 加权黄金

现在我们已经准备好了第一个简单的例子。在此示例中，我们估计静态系统的状态。静态系统是在合理的时间段内不会更改其状态的系统。例如，静态系统可以是一座塔，而状态将是它的高度。

在此示例中，我们估计金条的重量。我们有无偏尺度，即测量没有系统误差，但测量确实包括随机噪声。

系统是金条，系统状态是金条的重量。系统的动态模型是恒定的，因为我们假设权重在短时间内不会改变。

为了估计系统状态（即权重值），我们可以进行多次测量并对其进行平均。

在时间 n 时，估计值 $\hat{x}_{n,n}$ 将是所有先前测量值的平均值：

示例表示法：

$x$	是重量的真实值
$z_{n}$	是时间 $n$ 处重量的测量值
$\hat{x}_{n,n}$	是时间 $n$ 处 $x$ 的估计值（估计值是在进行测量 $z_{n}$ 后进行的）
$\hat{x}_{n+1,n}$	是 $x$ 的未来状态 $n+1$ 的估计值。估计是在 $n$ 时进行的。换句话说， $\hat{x}_{n+1,n}$ 是预测状态或外推状态
$\hat{x}_{n-1,n-1}$	是时间 $n-1$ 处 $x$ 的估计值（估计值是在进行测量 $z_{n-1}$ 后进行的）
$\hat{x}_{n,n-1}$	是先验预测 - 时间 $n$ 处状态的估计值。预测是在 $n-1$ 时进行的

注意：在文献中，变量上的插入符号（或帽子）表示估计值。

这个例子中的动态模型是静态的（或恒定的），因为黄金的重量不会随时间变化，因此 $\hat{x}_{n+1,n}= \hat{x}_{n,n}$ 。

虽然上述等式在数学上是正确的，但对于实现来说并不实用。为了估计 $\hat{x}_{n,n}$ ，我们需要记住所有历史测量值;因此，我们需要一个大内存。如果我们想在每次新测量后更新估计值，我们还需要反复重新计算平均值。因此，我们需要一个更强大的CPU。

仅保留最后一个估计值 $\hat{x}_{n-1,n-1}$ 并在每次新测量后更新它会更实用。下图举例说明了所需的算法：

根据测量和先前的预测估计当前状态。
使用动态模型根据当前状态估计预测下一个状态。

我们可以使用一个小的数学技巧来修改平均方程以满足我们的需要：

	笔记
	平均公式： $n$ 测量值的总和除以 $n$
	$n - 1$ 测量值加上最后一个测量值的总和除以 $n$
	扩大
	乘除项 $n - 1$
	重新排序 “橙色”项是先验估计值
	重写总和
	分配术语 $\frac{n-1}{n}$
	重新安排

$\hat{x}_{n-1,n-1}$ 是 $x$ 在时间 $n - 1$ 的估计状态，基于时间 $n - 1$ 。

让我们找到 $\hat{x}_{n,n-1}$ （时间 $n$ 的预测状态），基于 $\hat{x}_{n-1,n-1}$ （n - 1 时的估计）。换句话说，我们想将 $\hat{x}_{n-1,n-1}$ 外推到时间 n 。

由于此示例中的动态模型是静态的，因此 x 的预测状态等于 x 的估计状态： $\hat{x}_{n,n-1} = \hat{x}_{n-1,n-1}$ 。

基于上述，当前状态 $\hat{x}_{n,n}$ 的估计可以写成如下：

上述方程是五个卡尔曼滤波方程之一。它被称为状态更新方程。它的含义如下：

因子 $\frac{1}{n}$ 特定于我们的示例。我们稍后会讨论这个因子的重要作用，但现在，我想指出的是，在“卡尔曼滤波语言”中，这个因子被称为因素。它用 $K_{n}$ 表示。下标 n 表示卡尔曼增益可以随着每次迭代而变化。

$K_{n}$ 的发现是鲁道夫·卡尔曼的重要贡献之一。

在我们进入卡尔曼滤波器之前，我们使用希腊字母 $\alpha _{n}$ 而不是 $K_{n}$ 。

因此，状态更新公式如下所示：

术语 ( $z_{n} - \hat{x}_{n,n-1}$ )是“测量残差”，也称为创新。创新包含新信息。

在此示例中， $\frac{1}{n}$ 随着 n 的增加而减小。一开始，我们没有足够的关于当前状态的信息;因此，第一个估计基于第一个测量值 $\frac{1}{n}|_{n=1} = 1$ 。随着我们的继续，每个连续测量在估计过程中的权重较小，因为 $\frac{1}{n}$ 会减少。在某些时候，新测量的贡献将变得可以忽略不计。

让我们继续这个例子。在我们进行第一次测量之前，我们可以通过阅读金条上的印章来猜测（或粗略估计）金条重量。它被称为初始猜测，这是我们的第一个估计。

卡尔曼滤波器需要初始猜测作为预设，这可能非常粗糙。

估计算法

下图描述了此示例中使用的估计算法。

现在我们准备开始测量和估算过程。

数值示例

迭代零

初始化

我们对金条重量的初步猜测是 1000 克。初始猜测仅用于筛选器启动一次。因此，连续迭代不需要它。

预测

金条的重量不应该改变。因此，系统的动态模型是静态的。我们的下一个状态估计（预测）等于初始化：

第一次迭代

步骤 1

使用秤进行重量测量：

步骤 2

计算增益。在我们的示例中 $\alpha_{n}= \frac{1}{n}$ ，因此：

使用状态更新公式计算当前估计值：

注意：初始猜测可能是此特定示例中的任何数字。由于 $\alpha _{1}= 1$ ，因此在第一次迭代中消除了初始猜测。

步骤 3

系统的动态模型是静态的;

因此，金条的重量不应该改变。我们的下一个状态估计（预测）等于当前状态估计：

第二次迭代

单位时间延迟后，上一次迭代的预测估计值将成为当前迭代中的先前估计值：

步骤 1

对重量进行第二次测量：

步骤 2

计算增益：

计算当前估计：

步骤 3

第三次迭代

第四次迭代

第五次迭代

第六次迭代

第七次迭代

第八次迭代

第九次迭代

第十次迭代

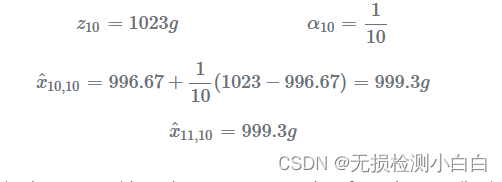
我们可以就此打住。增益随每次测量而降低。因此，每次连续测量的贡献都低于前一次测量的贡献。我们非常接近真实重量，即1000克。如果我们进行更多的测量，我们将更接近真实值。

下表总结了我们的测量值和估计值，图表比较了测量值、估计值和真实值。

结果分析

下图比较了真实值、测量值和估计值。

估计算法对测量值具有平滑效果，并收敛于真实值。

示例摘要

在此示例中，我们为静态系统开发了一个简单的估计算法。我们还推导出了状态更新方程，这是五个卡尔曼滤波方程之一。我们将在下一章中修改状态更新公式。

示例 2 – 在一个维度上跟踪等速飞机

是时候检查一个随时间改变其状态的动态系统了。在这个例子中，我们使用\（ $\alpha - \beta$ ）过滤器在一个维度上跟踪一个等速飞行器。

让我们假设一个一维的世界。我们假设飞机径向远离雷达（或朝向雷达）。在一维世界中，与雷达的角度是恒定的，飞行器高度是恒定的，如下图所示。

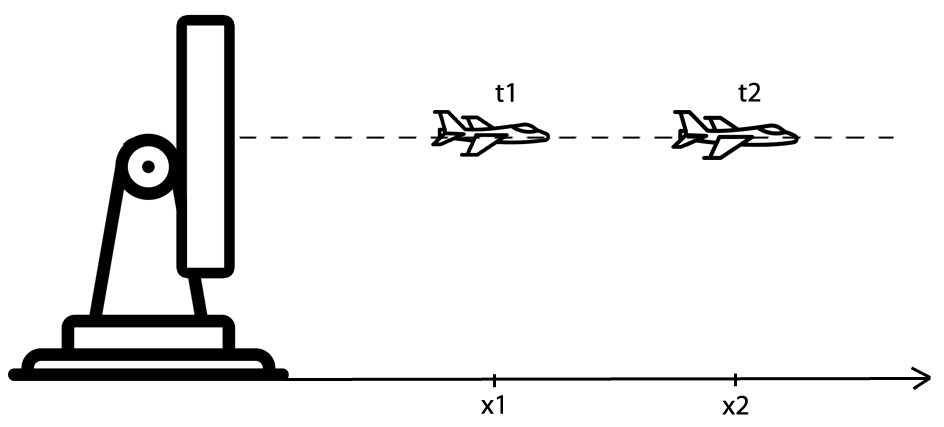
$x_{n}$ 表示在时间 n 到飞行器的距离。飞机速度可以使用距离微分法近似 - 测量距离随时间的变化。因此，速度是范围的导数：

雷达以恒定速率向目标方向发送跟踪波束。轨迹到轨迹间隔为 $\Delta t$ 。

两个运动方程描述了等速运动的系统动力学模型：

根据这些方程，飞机在下一个航迹周期的航程等于当前航迹周期的航程加上目标速度乘以航迹间间隔。由于我们在这个例子中假设速度是恒定的，所以下一个周期的速度等于当前周期的速度。

上述方程组称为状态外推方程（也称为转移方程或预测方程），也是五个卡尔曼滤波方程之一。该方程组将当前状态外推到下一个状态（预测）。

我们已经在前面的示例中使用了状态外推方程，其中我们假设下一个状态的权重等于当前状态的权重。

状态外推方程取决于系统动力学，并且因示例而异。

在矩阵表示法中，状态外推方程有一般形式。我们稍后再学习。

在这个例子中，我们使用上面特定于我们情况的方程。

注意：我们已经学习了五个卡尔曼滤波方程中的两个：

状态更新公式
- 状态外推方程

现在，我们将修改示例的状态更新公式。

$\alpha -\beta$ 过滤器

设雷达轨迹到轨迹（ $\Delta t$ ）周期为 5 秒。假设在时间 n-1 ，无人机（无人机）的估计射程为30，000m，估计无人机速度为40m/s。

使用状态外推方程，我们可以预测时间 n 的目标位置：

时间 n 的目标速度预测：

然而，在时间（n），雷达测量的距离（ $z_{n}$ ）为30，110m，而不是预期的30200m。预期（预测）距离与测量距离之间存在 90m 的差距。造成这种差距的可能原因有两个：

雷达测量不精确
飞机速度发生了变化。新的飞机速度为：

这两种说法中哪一种是正确的？

让我们写下速度的状态更新方程：

因子 $\beta$ 的值取决于雷达的精度水平。假设雷达的 $1\sigma$ 精度为 20m。预测距离和测量距离之间的 90 米差距很可能是由于飞机速度的变化造成的。在这种情况下，我们应该将 $\beta$ 因子设置为高值。如果我们设置 $\beta$ = 0.9，那么估计的速度将是：

另一方面，假设雷达的 $1\sigma$ 精度为 150m。那么90米的差距可能是雷达测量误差造成的。在这种情况下，我们应该将 $\beta$ 因子设置为较低的值。如果我们设置 $\beta$ = 0.1，那么估计的速度将是：

如果飞机速度从 40m/s 变为 22m/s，我们在 10 个轨迹循环后看到这一点（运行上述等式 10 次， $\beta$ = 0.1）。如果间隙是由测量误差引起的，则连续测量将在预测位置的前面或后面。因此，平均而言，目标速度不会改变。

飞机位置的状态更新公式类似于上一示例中推导的公式：

与前面的示例不同，在每次迭代中重新计算（ $\alpha ^{_{n}}=\frac{1}{n}$ ），在此示例中， $\alpha$ 因子是常数。

$\alpha$ 因子的大小取决于雷达测量精度。对于高精度雷达，我们应该选择高 $\alpha$ ，赋予测量高权重。如果 $\alpha$ = 1 ，则估计距离等于测量距离：

如果 $\alpha$ = 0 ，则测量没有意义：

因此，我们推导出了一个方程组，它构成了雷达跟踪器的状态更新方程。它们也称为 $\alpha -\beta$ 轨迹更新方程式或 $\alpha -\beta$ 轨迹滤波方程。

位置的状态更新公式：

速度的状态更新方程：

注意：在某些书籍中， $\alpha -\beta$ 过滤器称为注意：在某些书籍中，，其中希腊字母 $\alpha$ 替换为英文字母 g，英文字母 h 替换希腊字母 $\beta$ 。

注意：在这个例子中，我们从距离测量值（ $\dot{x}=\Delta x/\Delta t$ ）得出飞机速度。现代雷达可以直接使用多普勒效应测量径向速度。但是，我的目标是解释卡尔曼滤波器，而不是雷达操作。因此，为了概括起见，我将继续从我们示例中的距离测量中推导出速度。

估计算法

下图描述了此示例中使用的估计算法。

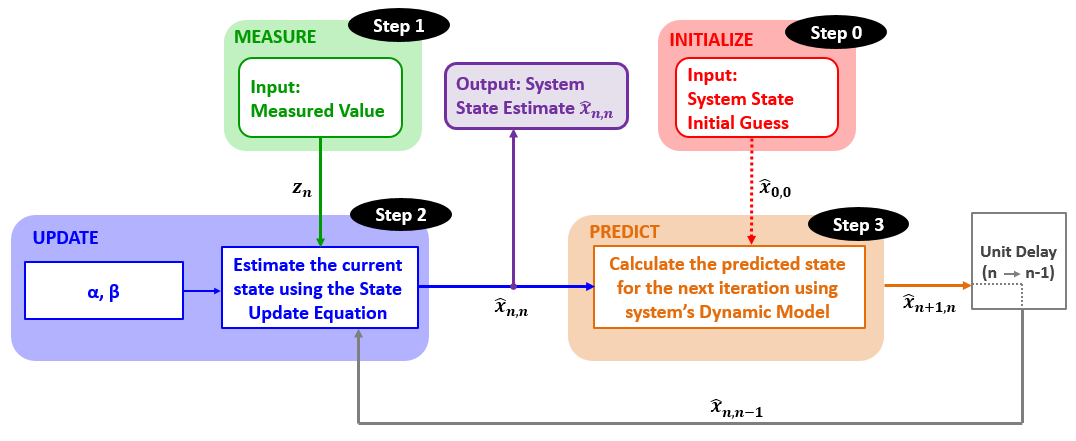
与前面的示例不同，此示例给出了增益值 $\alpha$ 和 $\beta$ 。对于卡尔曼滤波器， $\alpha$ 和 $\beta$ 被卡尔曼增益替换，卡尔曼增益在每次迭代时计算，但我们稍后会学习。

现在我们准备开始一个数值示例。

数值示例

考虑一维世界中的飞机径向向（或远离）雷达移动。

$\alpha - \beta$ 过滤器参数为：

$\alpha =0.2$ 。
$\beta =0.1$ 。

轨迹到轨迹的间隔为 5 秒。

注意：在本例中，我们使用不精确的雷达和低速目标（UAV）来更好地表示图形。雷达在现实生活中通常更精确，目标可以更快。

迭代零

初始化

给出时间 $n=0 \$ 的初始条件：

注意：轨迹启动（或我们如何获得初始条件）是一个重要的主题，稍后将讨论。现在，我们的目标是了解基本的 $\alpha - \beta$ 过滤器操作，所以让我们假设初始条件是由其他人给出的。

预测

初始猜测应使用状态外推方程外推到第一个周期（ $n=1$ ）：

第一次迭代

在第一个循环（ $n = 1$ ）中，初始猜测是先验估计：

步骤 1

雷达测量飞机航程：

步骤 2

使用状态更新公式计算当前估计值：

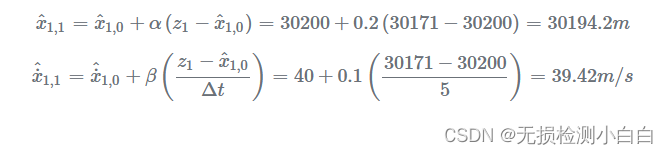
步骤 3

使用状态外推方程计算下一个状态估计值：

第二次迭代

单位时间延迟后，上一次迭代的预测估计值将成为当前迭代中的先前估计值：

步骤 1

雷达测量飞机航程：

步骤 2

使用状态更新公式计算当前估计值：

步骤 3

使用状态外推方程计算下一个状态估计值：

第三次迭代

第四次迭代

第五次迭代

第六次迭代

第七次迭代

第八次迭代

第九次迭代

第十次迭代

下表总结了我们的测量和估计值。

结果分析

下图比较了真实值、测量值和估计值。

我们的估计算法对测量值具有平滑效果，并收敛到真实值。

使用高 $\alpha$ 和 $\beta$

下图描述了 $\alpha$ = 0.8 和 $\beta$ = 0.5 的真实值、测量值和估计值。

此过滤器的“平滑”程度要低得多。“当前估计值”非常接近测量值，预测估计误差相对较高。

那么，我们是否应该始终为 $\alpha \$ 和 $\beta \$ 选择低值？

答案是否定的。 $\alpha \$ 和 $\beta \$ 的值应取决于测量精度。如果我们使用高精度设备，如激光雷达，我们更喜欢高 $\alpha \$ 和 $\beta \$ 跟随测量。在这种情况下，滤波器将快速响应目标的速度变化。另一方面，如果测量精度较低，我们更喜欢低 $\alpha \$ 和 $\beta \$ 。在这种情况下，滤波器可以平滑测量中的不确定性（误差）。然而，滤波器对目标速度变化的反应会慢得多。

示例摘要

我们推导出了 $\alpha - \beta$ 过滤器状态更新公式。我们还学习了状态外推方程。我们开发了一种基于 $\alpha - \beta$ 滤波器的一维动态系统估计算法，并求解了一个恒速目标的数值示例。

示例 3 – 在一个维度上跟踪加速的飞机

在这个例子中，我们使用 $\alpha - \beta$ 滤波器跟踪以恒定加速度移动的飞机。

在前面的示例中，我们跟踪了以 40m/s 的恒定速度移动的无人机。下图描述了目标范围和速度与时间的关系。

如您所见，距离函数是线性的。

现在让我们检查一下战斗机。这架飞机以50m/s的恒定速度移动20秒。然后飞机以8m/s的恒定加速度加速2再过 35 秒。

下图描述了目标距离、速度和加速度与时间的关系。

从图表中可以看出，飞机速度在前 20 秒内保持不变，然后线性增长。距离在前 20 秒线性增长，然后二次增长。

我们将使用上一个示例中使用的 $\alpha - \beta$ 过滤器跟踪这架飞机。

数值示例

考虑一维世界中的飞机径向向（或远离）雷达移动。

$\alpha - \beta$ 过滤器参数为：

$\alpha =0.2$
$\beta =0.1$

轨迹到轨迹的间隔为 5 秒。

迭代零

初始化

给出时间 $n=0$ 的初始条件：

预测

初始猜测应使用状态外推方程外推到第一个循环（ n=1 ）：

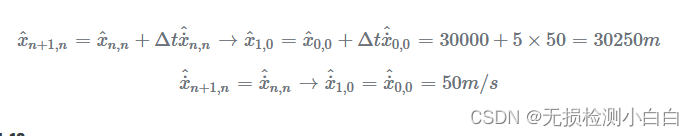
迭代 1-10

下表汇总了所有滤波器迭代：

结果分析

以下图表比较了前 75 秒范围内和速度的真实值、测量值和估计值。

您可以看到真实值或测量值与估计值之间存在恒定的差距。该间隙称为滞后误差。滞后错误的其他常见名称包括：

动态误差
系统误差
偏置误差
截断错误

在加速期间出现滞后错误。在加速周期之后，滤波器关闭间隙并收敛到真实值。但是，显著的滞后误差可能导致目标损耗。滞后误差在某些应用中是不可接受的，例如导弹制导或防空。

示例摘要

我们已经检查了目标加速度引起的滞后误差。

示例 4 – 使用 $\alpha -\beta -\gamma$ 滤波器跟踪加速的飞机

在这个例子中，我们使用 $\alpha -\beta -\gamma$ 过滤器跟踪飞机。

飞机以恒定的加速度移动。

$\alpha -\beta -\gamma$ 过滤器

$\alpha -\beta -\gamma$ 滤波器（有时称为 g-h-k 滤波器）考虑目标加速度。

因此，状态外推方程变为：

其中 $\ddot{x}_{n}$ 是加速度 x 的二阶导数）。

状态更新公式变为：

数值示例

让我们以前面示例中的场景为例：一架飞机以 50m/s 的恒定速度移动 20 秒，然后以 8m/s 的恒定加速度加速2再过 35 秒。

$\alpha - \beta - \gamma$ 过滤器参数为：

$\alpha = 0.5$
$\beta = 0.4.$
$\gamma = 0.1.$

轨迹到轨迹的间隔为 5 秒。

注意：我们使用不精确的雷达和低速目标来获得更好的图形表示。雷达在现实生活中通常更精确，目标可以更快。

迭代零

初始化

给出时间 n=0 的初始条件：

预测

初始猜测应使用状态外推方程外推到第一个周期（ n=1 ）：

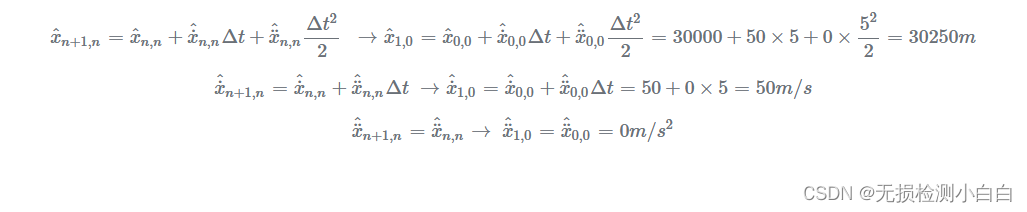
第一次迭代

在第一个循环（ n=1）中，初始猜测是先验估计：

步骤 1

雷达测量飞机航程：

步骤 2

使用状态更新公式计算当前估计值：

步骤 3

使用状态外推方程计算下一个状态估计值：

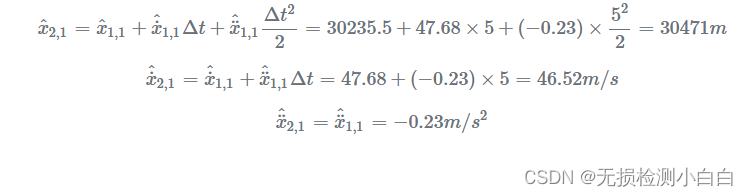
第二次迭代

在单位时间延迟之后，来自上述迭代的预测估计值将成为当前迭代中的先前估计值。

步骤 1

雷达测量飞机航程：

步骤 2

使用状态更新公式计算当前估计值：

步骤 3

使用状态外推方程计算下一个状态估计值：

迭代 3-10

下表汇总了连续迭代的计算：

结果分析

以下图表比较了前 50 秒的范围、速度和加速度的真实值、测量值和估计值。

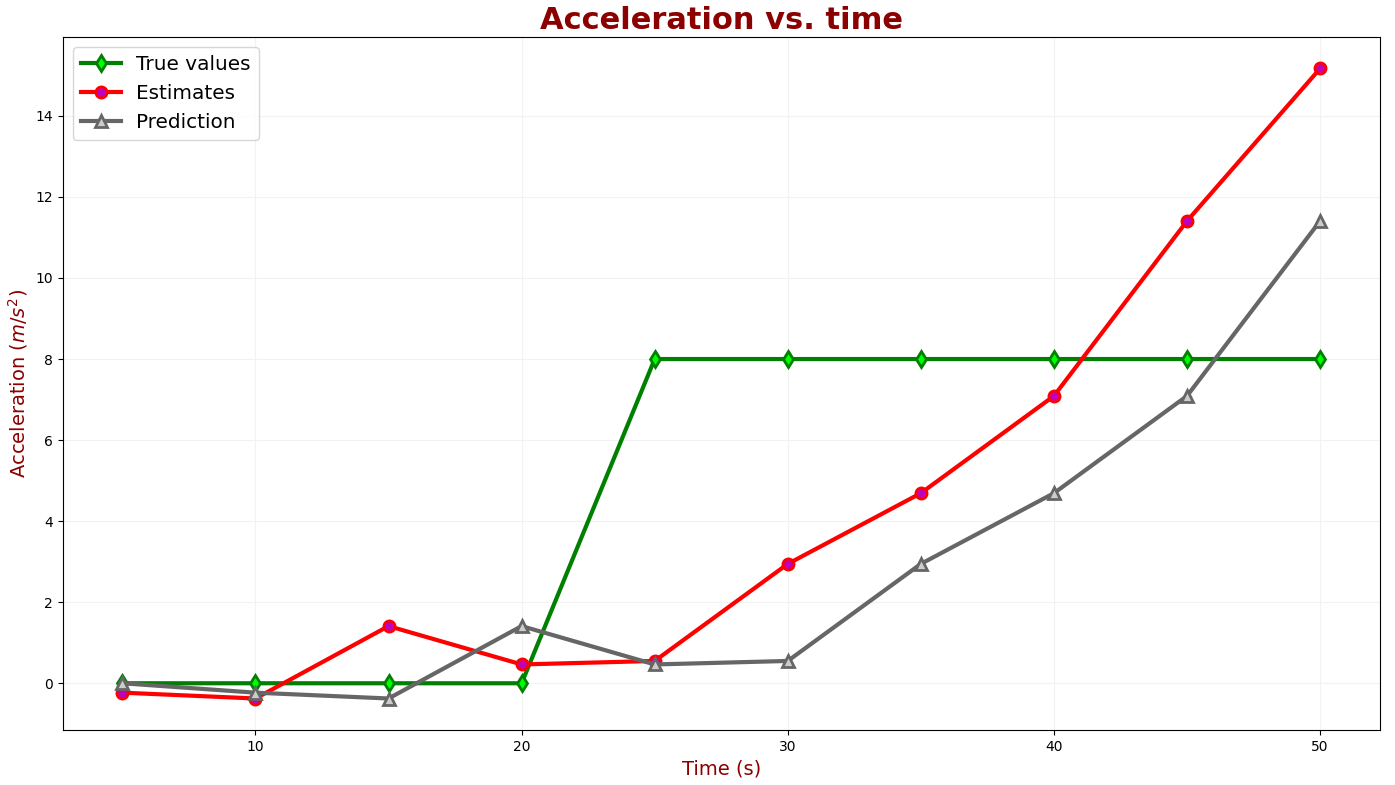
示例摘要

如您所见，具有包含加速度的动态模型方程的 $\alpha -\beta -\gamma$ 滤波器可以以恒定加速度跟踪目标并消除滞后误差。

但是在机动目标的情况下会发生什么？目标可以通过机动突然改变飞行方向。目标的动态模型还可以包括颠簸（改变加速度）。在这种情况下，具有常量 $\alpha -\beta -\gamma$ 系数的 $\alpha -\beta -\gamma$ 滤波器会产生估计误差，并且在某些情况下会丢失目标轨迹。

卡尔曼滤波器可以处理动态模型中的不确定性。这是我们的下一个主题，紧随总结之后。

$\alpha -\beta - (\gamma)$ 过滤器的摘要

有许多类型的 $\alpha -\beta - (\gamma)$ 过滤器，它们基于相同的原理：

当前状态估计基于状态更新公式。
以下状态估计（预测）基于动态模型方程。

这些滤波器之间的主要区别在于权重系数的选择 $\alpha -\beta - (\gamma)$ 。某些过滤器类型使用恒定加权系数;其他人计算每个过滤器迭代（周期）的加权系数。

选择 $\alpha$ 、 $\beta$ 和 $\gamma$ 对于估计算法的正确功能至关重要。

$\alpha -\beta - (\gamma)$ 参数应该是什么？

我将 $\alpha -\beta - (\gamma)$ 滤波器描述为卡尔曼滤波器的介绍，因此，我不会讨论这个主题。好奇的读者可以找到许多关于这个主题的书籍和论文。作为参考，我会推荐以下内容：

德克·坦纳，塔伦拉杰·辛格。“ $\alpha -\beta - (\gamma)$ 滤波器的优化设计”。纽约州立大学布法罗分校。

另一个重要问题是过滤器的启动，即为第一次过滤器迭代提供初始值。

以下列表包括最流行的 $\alpha -\beta - (\gamma)$ 滤波器：

维纳过滤器
贝叶斯滤波器
衰落记忆多项式滤波器
扩展内存（或增长内存）多项式滤波器
最小二乘过滤器
本尼迪克特-博德纳滤波器
集总过滤器
折扣最小二乘 \（ \alpha -\beta \）过滤器
临界阻尼 \（ \alpha -\beta \）滤波器
增长内存筛选器
卡尔曼滤波器
扩展卡尔曼滤波器
无味卡尔曼滤波器
扩展复数卡尔曼滤波器
高斯-埃尔米特卡尔曼滤波器
古巴卡尔曼滤波器
粒子过滤器

我希望写一个关于其中一些过滤器的教程。但本教程是关于卡尔曼滤波器的，这是以下示例的主题。

无损检测小白白

关注

3
点赞
踩
17

收藏

觉得还不错? 一键收藏
0
评论
卡尔曼滤波器简介——α−β−γ滤波器

卡尔曼滤波器简介——α−β−γ滤波器
复制链接

扫一扫

专栏目录

卡尔曼滤波器简介——α−β−γ滤波器

原文：The alpha - beta - gamma filter (kalmanfilter.net)

本章是介绍性的，它描述了α−β和α−β−γ滤波器。这些滤波器经常用于时间序列数据平滑。α−β-(γ)滤波的原则与卡尔曼滤波原理密切相关。

示例 1 – 加权黄金

估计算法

数值示例

结果分析

示例摘要

示例 2 – 在一个维度上跟踪等速飞机

过滤器

估计算法

数值示例

结果分析

示例摘要

示例 3 – 在一个维度上跟踪加速的飞机

数值示例

结果分析

示例摘要

示例 4 – 使用滤波器跟踪加速的飞机

数值示例

结果分析

示例摘要

过滤器的摘要

“相关推荐”对你有帮助么？

$\alpha -\beta$ 过滤器

示例 4 – 使用 $\alpha -\beta -\gamma$ 滤波器跟踪加速的飞机

$\alpha -\beta - (\gamma)$ 过滤器的摘要