PCA分析及CNS级别作图

 

从这节开始，就逐渐涉及转录组的基本可视化了，我们的可视化要做到CNS级别的图，争取做好分析，一步到位，让您有真正的收获！

PCA（主成分分析），具体的原理就不说了，自行百度。简单理解，PCA就是降维，将多维数据在2为平面理解和可视化。在转录组中的作用则是可以看出样本组间是否有差异，或者样本的一致性。组间差异大则两组分的开，反之则是差别不是很大。

示例数据用上节下载的GSE125424芯片数据表达矩阵，读入数据，并对数据进行初步的处理。

setwd("F:/生物信息学")
A <- read.table("GSE125424_series_matrix.txt",header = T,
                row.names = 1,sep = "\t",comment.char = "!")#这里注意，下载的芯片数据开有结尾包含有注释行，都是以！开头，所以要去除这些行
data <- t(A)#PCA分析需要将表达矩阵转置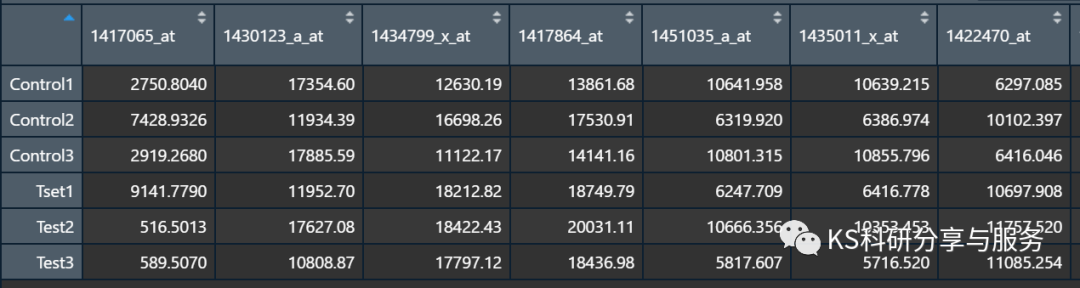   

PCA分析很简单，只需要一个函数就可以搞定。prcomp（）就可以，然后导出分析结果。

###PCA分析
data.pca <- prcomp(data, scale. = T)  #这是后续作图的文件
#输出特征向量
write.table(data.pca$rotation, file="PC.xls", quote=F, sep = "\t")
#输出新表
write.table(predict(data.pca), file="newTab.xls", quote=F, sep = "\t")
#输出PC比重
pca.sum=summary(data.pca)
write.table(pca.sum$importance, file="importance.xls", quote=F, sep = "\t")

接着就是PCA分析结果的可视化了，这里我们提供了两种方法。

1、factoextra包

加载包：

library(factoextra)

设置分组：

group=c(rep("Control",3),rep("Test",3))

可视化，由于factoextra是ggplot2的，所以在画完图后可以用ggplot2的方式进行修饰。

fviz_pca_ind(data.pca,
             col.ind=group,
             mean.point=F,
             addEllipses = T, 
             legend.title="Groups",
             ellipse.type="confidence",
             ellipse.level=0.9,
             palette = c("#CC3333", "#339999"))+ #Cell配色哦
  theme(panel.border = element_rect(fill=NA,color="black", size=1, linetype="solid"))#加个边框

结果很完美，非常满意！

2、ggbiplot包

看这包的名字就知道和ggplot2脱不了干系，先安装：

ibrary(devtools)
install_github("vqv/ggbiplot")
library(ggbiplot)

画图，画图数据和上一个一样：

ggbiplot(data.pca,obs.scale = 1,var.scale = 1,
         groups = group,ellipse = T,var.axes = F) +
  scale_color_brewer(palette = "Set1")  +
  theme(legend.direction = 'horizontal',legend.position = 'top') +
  geom_vline(xintercept = c(0), linetype = 6,color = "black") +
  geom_hline(yintercept = c(0),linetype = 6,color = "black") +
  theme_bw() + theme(panel.grid = element_line(colour = NA))

同样看起来非常完美，赏心悦目有没有！

PCA分析和作图就是这么简单，你学会了吗？