三相并网逆变器PI控制——离网模式

三相并网逆变器离网控制

逆变器并离网控制基本区别

  三相并网逆变器并网状态下，其主要功能是向大电网输送电能。此时系统并网点电压被大电网钳位，因此只需控制逆变器输出满足功率要求的电流，即可实现控制目标，故该状态下并网逆变器一般等效为电流源。

  三相并网逆变器离网运行状态下，其主要功能是输出满足负荷运行条件的电压，此时系统输出电流全部由负载自身参数决定。因此该状态下并网逆变器一般等效为电压源。

离网逆变器基本拓扑结构

  下图为离网状态下的逆变器拓扑结构，这里用纯电阻代替纯阻性负载：

  以逆变器指向负载电流方向为电流参考正方向，即图中$i_a$所指方向为正方向。

$$\{\begin{array}{c}{U}_a-L\frac{d{i}_a}{dt}-i_{a}R-U_{Ca}=0\\ U_b-L\frac{d{i}_b}{dt}-i_{b}R-U_{Cb}=0\\ U_c-L\frac{d{i}_c}{dt}-i_{c}R-U_{Cc}=0\\ C\frac{d{u}_{Ca}}{dt}=i_a-i_{ga}\\ C\frac{d{u}_{Cb}}{dt}=i_b-i_{gb}\\ C\frac{d{u}_{Cc}}{dt}=i_c-i_{gc}\end{array}\text{\hspace{1em}(1)}$$
  整理可得：
$$\{\begin{array}{c}\frac{d{i}_a}{dt}=\frac{1}{L}{U}_a-\frac{R}{L}{i}_a-\frac{1}{L}{U}_{Ca}\\ \frac{d{i}_b}{dt}=\frac{1}{L}{U}_b-\frac{R}{L}{i}_b-\frac{1}{L}{U}_{Cb}\\ \frac{d{i}_c}{dt}=\frac{1}{L}{U}_c-\frac{R}{L}{i}_c-\frac{1}{L}{U}_{Cc}\\ \frac{d{u}_{Ca}}{dt}=\frac{1}{C}{i}_a-\frac{1}{C}{i}_{ga}\\ \frac{d{u}_{Cb}}{dt}=\frac{1}{C}{i}_b-\frac{1}{C}{i}_{gb}\\ \frac{d{u}_{Cc}}{dt}=\frac{1}{C}{i}_c-\frac{1}{C}{i}_{gc}\end{array}\text{\hspace{1em}(2)}$$

  写成矩阵形式为：

$$\{\begin{array}{c}\left[\begin{array}{c}\frac{d{i}_a}{dt}\\ \frac{d{i}_b}{dt}\\ \frac{d{i}_c}{dt}\end{array}\right]=\frac{1}{L}\left[\begin{array}{c}{U}_a\\ U_b\\ U_c\end{array}\right]-\frac{R}{L}\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]-\frac{1}{L}\left[\begin{array}{c}{U}_{Ca}\\ U_{Cb}\\ U_{Cc}\end{array}\right]\\ \left[\begin{array}{c}\frac{d{U}_{Ca}}{dt}\\ \frac{d{U}_{Cb}}{dt}\\ \frac{d{U}_{Cc}}{dt}\end{array}\right]=\frac{1}{C}\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]-\frac{1}{C}\left[\begin{array}{c}{i}_{ga}\\ i_{gb}\\ i_{gc}\end{array}\right]\end{array}\text{\hspace{1em}(3)}$$

$\alpha \beta$坐标系下逆变器方程

  又已知abc-$\alpha \beta$正逆变换矩阵为：
$$\left[\begin{array}{c}{U}_{\alpha }\\ U_{\beta }\\ U_0\end{array}\right]=T_{abc-\alpha \beta }\left[\begin{array}{c}{U}_a\\ U_b\\ U_c\end{array}\right]=\frac{2}{3}\times \left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\\ 1& 1& 1\end{array}\right]\left[\begin{array}{c}{U}_a\\ U_b\\ U_c\end{array}\right]\text{\hspace{1em}(4)}$$

$$\left[\begin{array}{c}{U}_a\\ U_b\\ U_c\end{array}\right]=T_{\alpha \beta -abc}\left[\begin{array}{c}{U}_{\alpha }\\ U_{\beta }\\ U_0\end{array}\right]=\left[\begin{array}{ccc}1& 0& \frac{1}{2}\\ -\frac{1}{2}& \frac{\sqrt{3}}{2}& \frac{1}{2}\\ -\frac{1}{2}& -\frac{\sqrt{3}}{2}& \frac{1}{2}\end{array}\right]\left[\begin{array}{c}{U}_{\alpha }\\ U_{\beta }\\ U_0\end{array}\right]\text{\hspace{1em}(5)}$$

  这里补充了0轴是为了使变换矩阵变成方阵，利于求逆，实际上0轴不参与控制运算使用。

  对式（3）两边同时乘以$T_{abc-\alpha \beta }$即可将逆变器方程变换到$\alpha \beta$坐标系下，可得：
$$\begin{array}{c}{T}_{abc-\alpha \beta }\left[\begin{array}{c}\frac{d{i}_a}{dt}\\ \frac{d{i}_b}{dt}\\ \frac{d{i}_c}{dt}\end{array}\right]=\frac{1}{L}{T}_{abc-\alpha \beta }\left[\begin{array}{c}{U}_a\\ U_b\\ U_c\end{array}\right]-\frac{R}{L}{T}_{abc-\alpha \beta }\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]-\frac{1}{L}{T}_{abc-\alpha \beta }\left[\begin{array}{c}{U}_{Ca}\\ U_{Cb}\\ U_{Cc}\end{array}\right]\end{array}$$

这里注意只有
$$\left[\begin{array}{c}{U}_{\alpha }\\ U_{\beta }\\ U_0\end{array}\right]=T_{abc-\alpha \beta }\left[\begin{array}{c}{U}_a\\ U_b\\ U_c\end{array}\right]$$
因此$T_{abc-\alpha \beta }\left[\begin{array}{c}\frac{d{i}_a}{dt}\\ \frac{d{i}_b}{dt}\\ \frac{d{i}_c}{dt}\end{array}\right]$需要进行单独求取，求取过程如下：
$${\left[\begin{array}{c}{i}_{\alpha }\\ i_{\beta }\\ i_0\end{array}\right]}^{\prime }=(T_{abc-\alpha \beta }\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]{)}^{\prime }=(T_{abc-\alpha \beta }{)}^{\prime }\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]+(T_{abc-\alpha \beta })\left[\begin{array}{c}\frac{d{i}_a}{dt}\\ \frac{d{i}_b}{dt}\\ \frac{d{i}_c}{dt}\end{array}\right]$$

因此
$$T_{abc-\alpha \beta }\left[\begin{array}{c}\frac{d{i}_a}{dt}\\ \frac{d{i}_b}{dt}\\ \frac{d{i}_c}{dt}\end{array}\right]=(T_{abc-\alpha \beta }\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]{)}^{\prime }-(T_{abc-\alpha \beta }{)}^{\prime }\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]$$
而$(T_{abc-\alpha \beta })$为常数矩阵，因此
$$(T_{abc-\alpha \beta }{)}^{\prime }=0$$

所以：
$$T_{abc-\alpha \beta }\left[\begin{array}{c}\frac{d{i}_a}{dt}\\ \frac{d{i}_b}{dt}\\ \frac{d{i}_c}{dt}\end{array}\right]=\left[\begin{array}{c}\frac{d{i}_{\alpha }}{dt}\\ \frac{d{i}_{\beta }}{dt}\\ \frac{d{i}_0}{dt}\end{array}\right]$$
同理可得：
$$\{\begin{array}{c}\left[\begin{array}{c}\frac{d{i}_{\alpha }}{dt}\\ \frac{d{i}_{\beta }}{dt}\\ \frac{d{i}_0}{dt}\end{array}\right]=\frac{1}{L}\left[\begin{array}{c}{U}_{\alpha }\\ U_{\beta }\\ U_0\end{array}\right]-\frac{R}{L}\left[\begin{array}{c}{i}_{\alpha }\\ i_{\beta }\\ i_0\end{array}\right]-\frac{1}{L}\left[\begin{array}{c}{U}_{C\alpha }\\ U_{C\beta }\\ U_{C0}\end{array}\right]\\ \left[\begin{array}{c}\frac{d{U}_{C\alpha }}{dt}\\ \frac{d{U}_{C\beta }}{dt}\\ \frac{d{U}_{C0}}{dt}\end{array}\right]=\frac{1}{C}\left[\begin{array}{c}{i}_{\alpha }\\ i_{\beta }\\ i_0\end{array}\right]-\frac{1}{C}\left[\begin{array}{c}{i}_{g\alpha }\\ i_{g\beta }\\ i_{g0}\end{array}\right]\end{array}\text{\hspace{1em}(6)}$$

dq坐标系下逆变器方程

  又已知$\alpha \beta$-dq正逆变换矩阵为：
$$\left[\begin{array}{c}{U}_d\\ U_q\end{array}\right]=T_{\alpha \beta -dq}\left[\begin{array}{c}{U}_{\alpha }\\ U_{\beta }\end{array}\right]=\left[\begin{array}{cc}cos\phi & sin\phi \\ -sin\phi & cos\phi \end{array}\right]\left[\begin{array}{c}{U}_{\alpha }\\ U_{\beta }\end{array}\right]$$

$$\left[\begin{array}{c}{U}_{\alpha }\\ U_{\beta }\end{array}\right]=T_{dq-\alpha \beta }\begin{array}{c}{U}_d\\ U_q\end{array}=\left[\begin{array}{cc}cos\phi & -sin\phi \\ sin\phi & cos\phi \end{array}\right]\left[\begin{array}{c}{U}_d\\ U_q\end{array}\right]$$

  将上述$\alpha \beta$坐标下逆变器方程去掉0轴方程，并同时乘以变换矩阵$T_{\alpha \beta -dq}$可得：
$$T_{\alpha \beta -dq}\left[\begin{array}{c}\frac{d{i}_{\alpha }}{dt}\\ \frac{d{i}_{\beta }}{dt}\end{array}\right]=\frac{1}{L}{T}_{\alpha \beta -dq}\left[\begin{array}{c}{U}_{\alpha }\\ U_{\beta }\end{array}\right]-\frac{R}{L}{T}_{\alpha \beta -dq}\left[\begin{array}{c}{i}_{\alpha }\\ i_{\beta }\end{array}\right]-\frac{1}{L}{T}_{\alpha \beta -dq}\left[\begin{array}{c}{U}_{C\alpha }\\ U_{C\beta }\end{array}\right]$$
  同上述过程，需要求取$T_{\alpha \beta -dq}\left[\begin{array}{c}\frac{d{i}_{\alpha }}{dt}\\ \frac{d{i}_{\beta }}{dt}\end{array}\right]$,此时$\phi =\omega t$ ,$(T_{\alpha \beta -dq}{)}^{\prime }$ 不再为0。
$$(T_{\alpha \beta -dq}{)}^{\prime }=\left[\begin{array}{cc}-\omega sin\phi & \omega cos\phi \\ -\omega cos\phi & -\omega sin\phi \end{array}\right]$$

$$\begin{gathered} T_{\alpha \beta -dq}\left[\begin{array}{c}\frac{d{i}_{\alpha }}{dt}\\ \frac{d{i}_{\beta }}{dt}\end{array}\right]==\left[\begin{array}{c}\frac{d{i}_d}{dt}\\ \frac{d{i}_q}{dt}\end{array}\right]-\left[\begin{array}{cc}-\omega sin\phi & \omega cos\phi \\ -\omega cos\phi & -\omega sin\phi \end{array}\right]\left[\begin{array}{c}{i}_{\alpha }\\ i_{\beta }\end{array}\right]=\left[\begin{array}{cc}-\omega sin\phi & \omega cos\phi \\ -\omega cos\phi & -\omega sin\phi \end{array}\right](T_{\alpha \beta -dq}{)}^{-1}\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right] \\ =\left[\begin{array}{cc}-\omega sin\phi & \omega cos\phi \\ -\omega cos\phi & -\omega sin\phi \end{array}\right](T_{\alpha \beta -dq}{)}^{-1}\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]=\omega \left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right] \end{gathered}$$

   代入系统方程可得dq坐标系下的逆变器方程为：
$$\{\begin{array}{c}\left[\begin{array}{c}\frac{d{i}_d}{dt}\\ \frac{d{i}_q}{dt}\end{array}\right]=\frac{1}{L}\left[\begin{array}{c}{U}_d\\ U_q\end{array}\right]-\frac{R}{L}\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]-\frac{1}{L}\left[\begin{array}{c}{U}_{Cd}\\ U_{Cq}\end{array}\right]+\omega \left[\begin{array}{c}{i}_q\\ -i_d\end{array}\right]\\ \left[\begin{array}{c}\frac{d{U}_{Cd}}{dt}\\ \frac{d{U}_{Cq}}{dt}\end{array}\right]=\frac{1}{C}\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]-\frac{1}{C}\left[\begin{array}{c}{i}_{gd}\\ i_{gq}\end{array}\right]+\omega \left[\begin{array}{c}{U}_{Cq}\\ -U_{Cd}\end{array}\right]\end{array}\text{\hspace{1em}(7)}$$
  此时可以发现系统d轴方程存在与q轴耦合的现象，因此需要对系统进行精确控制需要进行dq轴解耦。

对式（7）进行拉普拉斯变换可得：
$$\{\begin{array}{c}{i}_d=i_{gd}+sC{U}_{Cd}-\omega C{U}_{Cq}\\ i_q=i_{gq}+sC{U}_{Cq}+\omega C{U}_{Cd}\\ U_d=(sL+R)i_d+U_{Cd}-\omega L{i}_q\\ U_q=(sL+R)i_q+U_{Cq}+\omega L{i}_d\end{array}\text{\hspace{1em}(8)}$$

用式（8）可以绘制如下框图。

  根据逆变器本体模型可以设置双PI控制原理图，因为通过解耦后结合PI控制器即可实现精准控制。

并网逆变器PI控制器定值跟踪

对于PI控制器
$$\begin{gathered} G_{(s)}=K_P(1+\frac{K_i}{s})=\frac{K_{P}s+K_P{K}_i}{s} \\ G(j\omega )=\frac{K_{P}j\omega +K_P{K}_i}{j\omega } \end{gathered}$$
因此：
$$G(j0)=\frac{K_{P}j0+K_P{K}_i}{j0}=\infty$$
此时闭环传函为：
$$A=\frac{G_{(j0)}}{1+G_{(j0)}}=1$$
所以 PI控制器对频率为0的信号（直流信号）可以实现无静差跟踪！因此在以上过程中需要将逆变器控制模型变换到dq轴，因为dq变换是以PLL输出电压角度进行变换，所以三相电流在dq坐标系下（d轴分量为电流幅值，q轴分量为零）。解耦是为了消除其他轴对PI控制的影响。

仿真结果

SPWM调制信号：

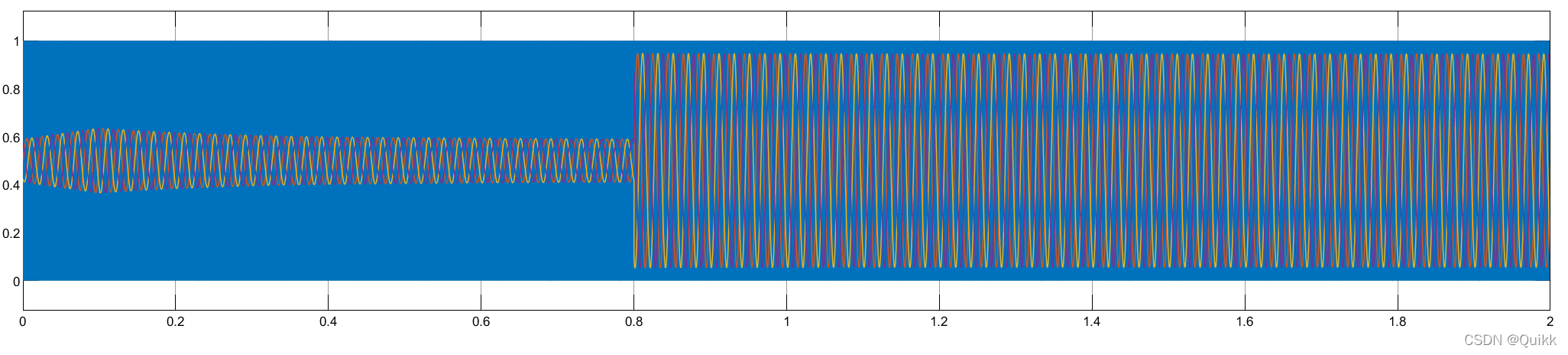
输出线电压（未滤波器前）：

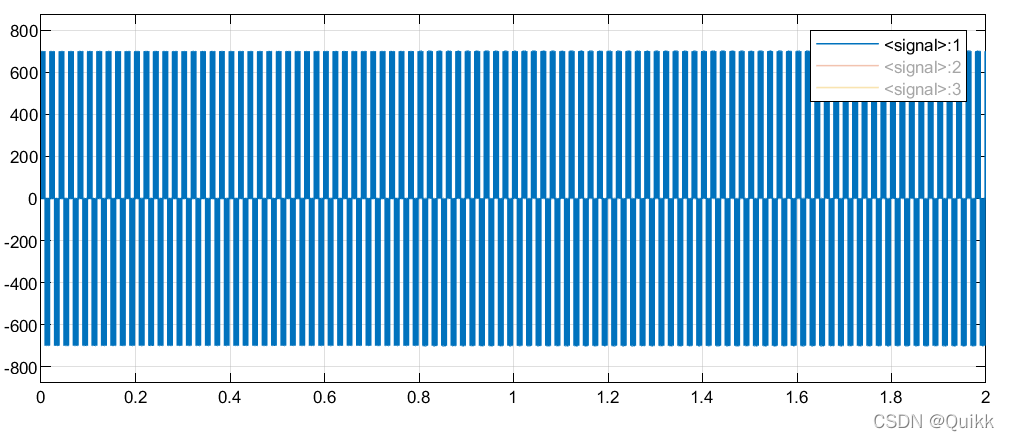
负载侧相电压（0.1s并网，0.8s给定功率阶跃）：

输出功率：

仿真模型：模型链接