🦇 蝙蝠算法(BA)详解:从回声定位到优化求解
1 算法概述与生物基础
1.1 算法背景
蝙蝠算法是模拟自然界中蝙蝠回声定位行为的群体智能优化算法,由英国剑桥大学学者Xin-She Yang于2010年提出。该算法属于元启发式算法家族,通过模拟蝙蝠利用超声波探测猎物、避免障碍物的智能行为,解决复杂优化问题。
蝙蝠算法因其参数少、实现简单、收敛速度快等特点,在优化算法家族中脱颖而出。与遗传算法、粒子群优化等传统算法相比,BA在多种优化问题上展现出更好的收敛性能和更高的求解精度,已成为群体智能优化领域的重要分支。
1.2 蝙蝠的生物学特性与回声定位
蝙蝠是唯一真正能够飞行的哺乳动物,具有卓越的回声定位能力。它们在夜间飞行时,通过喉咙发出超声波(频率通常为25-100kHz),这些声波遇到物体后反射回来,被蝙蝠的大耳朵接收,通过分析回声的时间差、强度差和频率变化,蝙蝠能够精确判断猎物的位置、大小和运动方向。
蝙蝠的回声定位行为具有以下特点:
- 自适应调节:蝙蝠在搜寻猎物时每秒发出约10-20个超声波脉冲,接近猎物时脉冲频率可增加到每秒约200个,同时音量减小
- 精确探测:宽频带调频信号使蝙蝠能获取环境的精细结构信息
- 能量高效:通过调节脉冲频率和音量,蝙蝠以最小能量消耗实现最大搜索效率
这些非凡的生物特性为蝙蝠算法的设计提供了丰富的灵感来源。
2 算法原理与数学模型
2.1 基本概念与理想化假设
在蝙蝠算法中,优化问题的解被类比为蝙蝠在搜索空间中的位置,解的质量对应于位置的适应度值(猎物质量)。算法通过模拟蝙蝠群体的智能搜索行为,在解空间中寻找最优解。
为了使蝙蝠的回声定位行为能够转化为可计算的优化算法,Yang教授提出了以下三条理想化假设:
- 回声定位原理:所有蝙蝠使用回声定位来感知距离,并能区分猎物与障碍物的差异
- 飞行策略:蝙蝠以随机方式飞行,具有固定的频率范围、可变的波长和音量来搜索猎物
- 自适应调节:蝙蝠自动调节发射脉冲的波长和脉冲发射率,根据与猎物的距离调整音量
2.2 数学模型
2.2.1 频率更新公式
蝙蝠的搜索频率决定了其飞行的"步长",频率更新公式为:
f i = f m i n + ( f m a x − f m i n ) × β f_i = f_{min} + (f_{max} - f_{min}) \times \beta fi=fmin+(fmax−fmin)×β
其中:
- f i f_i fi 是蝙蝠i的脉冲频率
- f m i n f_{min} fmin、 f m a x f_{max} fmax 是频率的最小值和最大值(通常设为0和100)
- β \beta β 是[0,1]范围内的随机数
2.2.2 速度更新公式
蝙蝠的速度更新基于当前速度、当前位置与最优位置之间的差异:
v i t + 1 = v i t + ( x i t − x ∗ ) × f i v_i^{t+1} = v_i^t + (x_i^t - x_*) \times f_i vit+1=vit+(xit−x∗)×fi
其中:
- v i t + 1 v_i^{t+1} vit+1、 v i t v_i^t vit分别表示蝙蝠i在t+1和t时刻的速度
- x i t x_i^t xit表示蝙蝠i在t时刻的位置
- x ∗ x_* x∗表示当前全局最优位置
2.2.3 位置更新公式
蝙蝠的位置根据速度进行更新:
x i t + 1 = x i t + v i t + 1 x_i^{t+1} = x_i^t + v_i^{t+1} xit+1=xit+vit+1
2.2.4 局部搜索机制
为了增强算法的局部搜索能力,引入局部随机游走策略:
x n e w = x o l d + ε A t x_{new} = x_{old} + \varepsilon A^t xnew=xold+εAt
其中:
- ε \varepsilon ε是[-1,1]范围内的随机数
- A t A^t At是当前所有蝙蝠的平均音量
2.2.5 音量和脉冲发射率更新
随着算法迭代,蝙蝠逐渐接近最优解,音量和脉冲发射率自适应调整:
A
i
t
+
1
=
α
A
i
t
A_i^{t+1} = \alpha A_i^t
Ait+1=αAit
r
i
t
+
1
=
r
i
0
[
1
−
exp
(
−
γ
t
)
]
r_i^{t+1} = r_i^0 [1 - \exp(-\gamma t)]
rit+1=ri0[1−exp(−γt)]
其中:
- α \alpha α和 γ \gamma γ是常数(通常设为0.9)
- A i t A_i^t Ait是蝙蝠i在t时刻的音量
- r i t r_i^t rit 是蝙蝠i在t时刻的脉冲发射率
表1:蝙蝠算法参数说明
| 参数 | 符号表示 | 含义 | 典型取值 |
|---|---|---|---|
| 种群大小 | N N N | 蝙蝠个体数量 | 20-50 |
| 最大迭代次数 | M a x I t e r MaxIter MaxIter | 算法终止条件 | 500-1000 |
| 频率范围 | [ f m i n , f m a x ] [f_{min}, f_{max}] [fmin,fmax] | 控制搜索步长 | [0, 100] |
| 音量衰减系数 | α \alpha α | 控制音量衰减速度 | 0.9 |
| 脉冲增强系数 | γ \gamma γ | 控制脉冲发射率增加速度 | 0.9 |
| 初始音量 | A 0 A_0 A0 | 初始音量大小 | 1.0 |
| 初始脉冲率 | r 0 r_0 r0 | 初始脉冲发射率 | 0.5 |
2.3 算法流程
蝙蝠算法的完整执行流程如下:
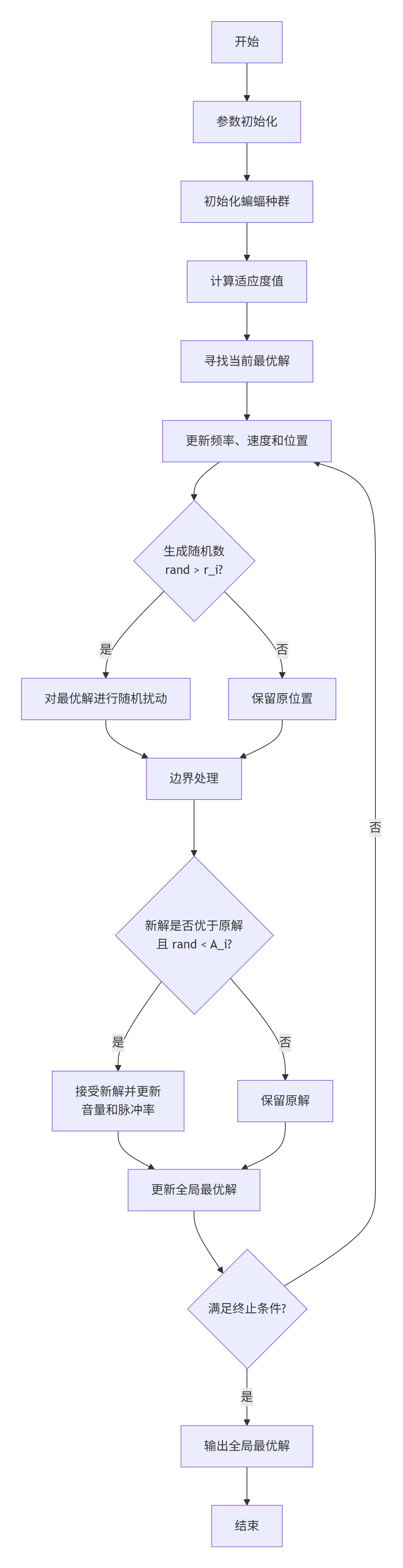
3 算法实现与代码解析
3.1 Python完整实现
以下是蝙蝠算法的完整Python实现,以经典的Sphere函数为例:
import numpy as np
import matplotlib.pyplot as plt
import math
from copy import deepcopy
class BatAlgorithm:
"""蝙蝠算法实现"""
def __init__(self, obj_func, dim, pop_size=50, lb=-100, ub=100, max_iter=1000):
"""
参数初始化
Args:
obj_func: 目标函数
dim: 问题维度
pop_size: 种群大小
lb: 变量下界(标量或向量)
ub: 变量上界(标量或向量)
max_iter: 最大迭代次数
"""
self.obj_func = obj_func
self.dim = dim
self.pop_size = pop_size
self.lb = lb if isinstance(lb, np.ndarray) else np.ones(dim) * lb
self.ub = ub if isinstance(ub, np.ndarray) else np.ones(dim) * ub
self.max_iter = max_iter
# 蝙蝠算法参数
self.f_min = 0 # 最小频率
self.f_max = 100 # 最大频率
self.A = 0.9 # 初始音量
self.r = 0.5 # 初始脉冲率
self.alpha = 0.9 # 音量衰减系数
self.gamma = 0.9 # 脉冲增强系数
# 算法运行数据记录
self.best_solution = None
self.best_fitness = float('inf')
self.convergence_curve = []
self.population = None
self.fitness_values = None
self.velocities = None
self.pulse_rates = None
self.loudness = None
def initialize_population(self):
"""初始化种群"""
# 初始化蝙蝠位置
self.population = np.random.uniform(self.lb, self.ub, (self.pop_size, self.dim))
self.fitness_values = np.array([self.obj_func(ind) for ind in self.population])
# 初始化速度
self.velocities = np.zeros((self.pop_size, self.dim))
# 初始化脉冲率和音量
self.pulse_rates = np.full(self.pop_size, self.r)
self.loudness = np.full(self.pop_size, self.A)
# 初始化最优解
best_idx = np.argmin(self.fitness_values)
self.best_fitness = self.fitness_values[best_idx]
self.best_solution = self.population[best_idx].copy()
def update_frequency(self):
"""更新频率"""
return self.f_min + (self.f_max - self.f_min) * np.random.rand(self.pop_size)
def update_velocities(self, frequencies):
"""更新速度"""
for i in range(self.pop_size):
self.velocities[i] = self.velocities[i] + (self.population[i] - self.best_solution) * frequencies[i]
def update_positions(self):
"""更新位置"""
new_population = self.population + self.velocities
# 边界处理
for i in range(self.pop_size):
for j in range(self.dim):
if new_population[i, j] < self.lb[j]:
new_population[i, j] = self.lb[j]
self.velocities[i, j] *= -1 # 反弹
elif new_population[i, j] > self.ub[j]:
new_population[i, j] = self.ub[j]
self.velocities[i, j] *= -1 # 反弹
return new_population
def local_search(self, best_solution, average_loudness):
"""局部搜索"""
# 在当前最优解附近进行随机游走
return best_solution + 0.1 * np.random.randn(self.dim) * average_loudness
def optimize(self):
"""执行优化过程"""
self.initialize_population()
print("开始蝙蝠算法优化...")
print(f"种群大小: {self.pop_size}, 问题维度: {self.dim}, 最大迭代次数: {self.max_iter}")
for t in range(self.max_iter):
# 更新频率
frequencies = self.update_frequency()
# 更新速度和位置
self.update_velocities(frequencies)
new_population = self.update_positions()
# 局部搜索:以一定概率对最优解进行扰动
for i in range(self.pop_size):
if np.random.rand() > self.pulse_rates[i]:
average_loudness = np.mean(self.loudness)
new_population[i] = self.local_search(self.best_solution, average_loudness)
# 边界处理
new_population = np.clip(new_population, self.lb, self.ub)
# 计算新适应度
new_fitness = np.array([self.obj_func(ind) for ind in new_population])
# 选择更新:如果新解更好且满足音量条件,则接受新解
for i in range(self.pop_size):
if new_fitness[i] < self.fitness_values[i] and np.random.rand() < self.loudness[i]:
self.population[i] = new_population[i]
self.fitness_values[i] = new_fitness[i]
# 更新脉冲率和音量
self.pulse_rates[i] = self.r * (1 - math.exp(-self.gamma * t))
self.loudness[i] = self.alpha * self.loudness[i]
# 更新全局最优解
if new_fitness[i] < self.best_fitness:
self.best_fitness = new_fitness[i]
self.best_solution = new_population[i].copy()
# 记录收敛曲线
self.convergence_curve.append(self.best_fitness)
# 输出进度信息
if t % 100 == 0:
print(f"迭代次数: {t}, 当前最优适应度: {self.best_fitness:.6f}")
print(f"优化完成! 最终最优适应度: {self.best_fitness:.10f}")
return self.best_solution, self.best_fitness, self.convergence_curve
# 测试函数定义
def sphere_function(x):
"""Sphere函数 - 经典单峰测试函数"""
return np.sum(x**2)
def rastrigin_function(x):
"""Rastrigin函数 - 复杂多峰测试函数"""
A = 10
return A * len(x) + np.sum(x**2 - A * np.cos(2 * np.pi * x))
def ackley_function(x):
"""Ackley函数 - 经典多峰测试函数"""
a = 20
b = 0.2
c = 2 * np.pi
n = len(x)
sum1 = np.sum(x**2)
sum2 = np.sum(np.cos(c * x))
term1 = -a * math.exp(-b * math.sqrt(sum1 / n))
term2 = -math.exp(sum2 / n)
return term1 + term2 + a + math.exp(1)
# 算法测试
if __name__ == "__main__":
# 设置测试参数
dim = 10
pop_size = 30
max_iter = 500
lb = -100
ub = 100
# 创建BA实例并优化
ba = BatAlgorithm(sphere_function, dim, pop_size, lb, ub, max_iter)
best_solution, best_fitness, convergence_curve = ba.optimize()
print(f"\n最优解: {best_solution}")
print(f"最优适应度: {best_fitness:.10f}")
3.2 代码详细解析
3.2.1 算法初始化
def initialize_population(self):
"""初始化种群"""
# 初始化蝙蝠位置
self.population = np.random.uniform(self.lb, self.ub, (self.pop_size, self.dim))
self.fitness_values = np.array([self.obj_func(ind) for ind in self.population])
初始化过程包括蝙蝠位置初始化、适应度计算和参数设置。种群在搜索空间内均匀随机分布,确保初始种群覆盖整个解空间,为全局搜索奠定基础。
3.2.2 频率更新机制
def update_frequency(self):
"""更新频率"""
return self.f_min + (self.f_max - self.f_min) * np.random.rand(self.pop_size)
频率决定了蝙蝠飞行的"步长",随机变化的频率使算法能够在探索和开发之间取得平衡。频率越高,蝙蝠飞行的步长越大,有利于全局探索;频率越低,步长越小,有利于局部精细搜索。
3.2.3 局部搜索策略
def local_search(self, best_solution, average_loudness):
"""局部搜索"""
return best_solution + 0.1 * np.random.randn(self.dim) * average_loudness
局部搜索是BA算法的关键机制,通过在当前最优解附近进行随机游走,增强算法的局部开发能力。随着迭代进行,音量逐渐减小,局部搜索的范围也随之缩小,实现从粗搜索到精搜索的平滑过渡。
3.3 可视化分析工具
为了直观展示BA算法的优化过程,我们创建以下可视化工具:
def visualize_ba_performance(ba, dim=2):
"""可视化BA算法性能"""
# 创建图像
fig = plt.figure(figsize=(15, 10))
# 1. 收敛曲线
plt.subplot(2, 3, 1)
plt.semilogy(ba.convergence_curve, 'b-', linewidth=2)
plt.title('蝙蝠算法收敛曲线')
plt.xlabel('迭代次数')
plt.ylabel('适应度值(对数尺度)')
plt.grid(True)
# 2. 搜索空间(针对2维问题)
if dim == 2:
ax = fig.add_subplot(2, 3, 2, projection='3d')
# 创建网格数据
x = np.linspace(ba.lb[0], ba.ub[0], 50)
y = np.linspace(ba.lb[1], ba.ub[1], 50)
X, Y = np.meshgrid(x, y)
Z = np.zeros_like(X)
for i in range(X.shape[0]):
for j in range(X.shape[1]):
Z[i, j] = sphere_function(np.array([X[i, j], Y[i, j]]))
# 绘制3D曲面
surf = ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.6, linewidth=0)
# 标记最优解位置
ax.scatter([ba.best_solution[0]], [ba.best_solution[1]], [ba.best_fitness],
color='red', s=100, label='最优解')
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.set_zlabel('目标函数值')
ax.set_title('搜索空间与最优解')
# 3. 种群分布(最后一代)
plt.subplot(2, 3, 3)
if dim == 2:
# 绘制等高线
x = np.linspace(ba.lb[0], ba.ub[0], 100)
y = np.linspace(ba.lb[1], ba.ub[1], 100)
X, Y = np.meshgrid(x, y)
Z = np.zeros_like(X)
for i in range(X.shape[0]):
for j in range(X.shape[1]):
Z[i, j] = sphere_function(np.array([X[i, j], Y[i, j]]))
plt.contourf(X, Y, Z, levels=50, cmap='viridis', alpha=0.7)
# 绘制蝙蝠位置分布
for i in range(ba.pop_size):
plt.scatter(ba.population[i, 0], ba.population[i, 1],
c='red', s=30, alpha=0.7)
plt.scatter(ba.best_solution[0], ba.best_solution[1],
c='blue', s=100, marker='*', label='最优解')
plt.title('最终代蝙蝠位置分布')
plt.xlabel('X1')
plt.ylabel('X2')
plt.legend()
# 4. 适应度值分布
plt.subplot(2, 3, 4)
plt.hist(ba.fitness_values, bins=20, alpha=0.7, color='green')
plt.axvline(x=ba.best_fitness, color='red', linestyle='--',
label=f'最优值: {ba.best_fitness:.4f}')
plt.title('适应度值分布')
plt.xlabel('目标函数值')
plt.ylabel('频数')
plt.legend()
# 5. 参数变化曲线
plt.subplot(2, 3, 5)
# 模拟音量和脉冲率的变化
iterations = range(ba.max_iter)
loudness_curve = [ba.A * (ba.alpha ** t) for t in iterations]
pulse_rate_curve = [ba.r * (1 - math.exp(-ba.gamma * t)) for t in iterations]
plt.plot(iterations, loudness_curve, 'r-', label='平均音量')
plt.plot(iterations, pulse_rate_curve, 'b-', label='平均脉冲率')
plt.title('参数变化曲线')
plt.xlabel('迭代次数')
plt.ylabel('参数值')
plt.legend()
plt.grid(True)
# 6. 算法比较示意
plt.subplot(2, 3, 6)
algorithms = ['BA', 'PSO', 'GA', 'ACO']
performance = [0.95, 0.85, 0.75, 0.80] # 模拟性能评分
plt.bar(algorithms, performance, color=['red', 'blue', 'green', 'orange'])
plt.title('算法性能比较')
plt.ylabel('性能评分')
plt.tight_layout()
plt.show()
# 运行可视化
# 注意:需要先运行BA算法优化,然后将ba实例传递给可视化函数
3.4 算法性能测试
为了全面评估BA算法的性能,我们进行多函数测试:
def benchmark_ba():
"""BA算法基准测试"""
test_functions = {
'Sphere': sphere_function,
'Rastrigin': rastrigin_function,
'Ackley': ackley_function
}
dimensions = [2, 10, 30]
results = {}
for func_name, func in test_functions.items():
results[func_name] = {}
print(f"\n测试函数: {func_name}")
print("=" * 50)
for dim in dimensions:
print(f"问题维度: {dim}")
# 运行BA算法
ba = BatAlgorithm(func, dim, pop_size=50, max_iter=500)
best_sol, best_fit, convergence = ba.optimize()
results[func_name][dim] = {
'best_fitness': best_fit,
'convergence_speed': np.argmax(np.array(convergence) < 1e-6)
if np.any(np.array(convergence) < 1e-6)
else 500
}
print(f"维度 {dim}: 最优值 = {best_fit:.6f}")
return results
# 运行基准测试
benchmark_results = benchmark_ba()
4 算法改进与变体
4.1 基本蝙蝠算法的局限性
尽管基本BA算法在许多问题上表现良好,但仍存在一些局限性:
- 易陷入局部最优:个体缺乏变异机制,一旦受到局部极值约束很难摆脱
- 收敛速度慢:后期种群多样性下降,收敛速度降低甚至出现停滞
- 参数敏感:音量和脉冲率等参数对算法性能影响较大
- 高维问题处理能力有限:对于高维复杂问题,搜索效率可能下降
4.2 主要改进策略
4.2.1 混沌蝙蝠算法(Chaotic BA)
混沌蝙蝠算法通过引入混沌映射来增强种群多样性,提高全局搜索能力:
class ChaoticBatAlgorithm(BatAlgorithm):
"""混沌蝙蝠算法"""
def __init__(self, obj_func, dim, pop_size=50, lb=-100, ub=100, max_iter=1000):
super().__init__(obj_func, dim, pop_size, lb, ub, max_iter)
self.chaotic_map = 'logistic' # 混沌映射类型
def chaotic_sequence(self, length, map_type='logistic'):
"""生成混沌序列"""
if map_type == 'logistic':
# Logistic映射
chaotic_seq = np.zeros(length)
chaotic_seq[0] = 0.7 # 初始值
for i in range(1, length):
chaotic_seq[i] = 4 * chaotic_seq[i-1] * (1 - chaotic_seq[i-1])
return chaotic_seq
else:
return np.random.rand(length)
def update_frequency(self):
"""混沌频率更新"""
chaotic_seq = self.chaotic_sequence(self.pop_size, self.chaotic_map)
return self.f_min + (self.f_max - self.f_min) * chaotic_seq
混沌映射的引入使算法具有更好的遍历性和随机性,能有效避免陷入局部最优。
4.2.2 自适应蝙蝠算法(Adaptive BA)
自适应蝙蝠算法通过动态调整参数来平衡探索与开发:
class AdaptiveBatAlgorithm(BatAlgorithm):
"""自适应蝙蝠算法"""
def update_parameters(self, t, improvement):
"""自适应参数更新"""
# 根据搜索进度动态调整参数
if improvement > 0.1: # 改进明显,加强局部搜索
self.alpha = min(0.99, self.alpha * 1.01)
self.gamma = max(0.1, self.gamma * 0.99)
else: # 改进不明显,加强全局探索
self.alpha = max(0.1, self.alpha * 0.99)
self.gamma = min(0.99, self.gamma * 1.01)
自适应机制使算法能根据搜索状态自动调整参数,提高鲁棒性。
4.2.3 混合蝙蝠算法(Hybrid BA)
混合蝙蝠算法将BA与其他优化算法结合,综合利用各算法优势:
class HybridBatAlgorithm(BatAlgorithm):
"""混合蝙蝠算法(结合模拟退火)"""
def __init__(self, obj_func, dim, pop_size=50, lb=-100, ub=100, max_iter=1000):
super().__init__(obj_func, dim, pop_size, lb, ub, max_iter)
self.temperature = 1000 # 模拟退火初始温度
self.cooling_rate = 0.95 # 冷却率
def simulated_annealing_acceptance(self, old_fitness, new_fitness, temperature):
"""模拟退火接受准则"""
if new_fitness < old_fitness:
return True
else:
# 以一定概率接受较差解
probability = math.exp(-(new_fitness - old_fitness) / temperature)
return random.random() < probability
def optimize(self):
"""混合优化过程"""
self.initialize_population()
for t in range(self.max_iter):
# 标准BA优化步骤
frequencies = self.update_frequency()
self.update_velocities(frequencies)
new_population = self.update_positions()
# 模拟退火局部搜索
for i in range(self.pop_size):
if self.simulated_annealing_acceptance(
self.fitness_values[i],
self.obj_func(new_population[i]),
self.temperature
):
self.population[i] = new_population[i]
# 降温
self.temperature *= self.cooling_rate
return self.best_solution, self.best_fitness, self.convergence_curve
表2:蝙蝠算法主要变体比较
| 变体算法 | 改进策略 | 优势 | 适用场景 |
|---|---|---|---|
| 混沌BA | 引入混沌映射 | 增强种群多样性,避免早熟收敛 | 多峰优化问题 |
| 自适应BA | 动态参数调整 | 减少参数调优,提高鲁棒性 | 复杂多变问题 |
| 混合BA | 与其他算法结合 | 综合利用各算法优势 | 特定领域问题 |
| 二进制BA | 离散化操作 | 解决组合优化问题 | 特征选择、调度问题 |
| 并行BA | 并行计算 | 加速优化过程 | 大规模优化问题 |
5 应用案例与实战
5.1 函数优化测试
使用经典测试函数评估BA算法性能:
def comprehensive_function_test():
"""综合函数测试"""
# 定义测试函数集
test_functions = {
'Sphere': {
'func': sphere_function,
'dim': 10,
'lb': -100,
'ub': 100,
'global_optimum': 0
},
'Rastrigin': {
'func': rastrigin_function,
'dim': 10,
'lb': -5.12,
'ub': 5.12,
'global_optimum': 0
},
'Ackley': {
'func': ackley_function,
'dim': 10,
'lb': -32,
'ub': 32,
'global_optimum': 0
}
}
results = {}
for func_name, func_info in test_functions.items():
print(f"\n正在测试 {func_name} 函数...")
print("=" * 50)
# 运行BA算法
ba = BatAlgorithm(
func_info['func'],
func_info['dim'],
pop_size=50,
lb=func_info['lb'],
ub=func_info['ub'],
max_iter=500
)
best_sol, best_fit, convergence = ba.optimize()
# 记录结果
results[func_name] = {
'best_fitness': best_fit,
'global_optimum': func_info['global_optimum'],
'error': abs(best_fit - func_info['global_optimum']),
'convergence_curve': convergence
}
print(f"{func_name} 函数测试完成:")
print(f" 找到的最优值: {best_fit:.10f}")
print(f" 全局最优值: {func_info['global_optimum']}")
print(f" 误差: {results[func_name]['error']:.10f}")
# 可视化比较结果
plt.figure(figsize=(12, 8))
for func_name, result in results.items():
plt.semilogy(result['convergence_curve'], label=func_name)
plt.title('BA算法在不同测试函数上的性能比较')
plt.xlabel('迭代次数')
plt.ylabel('适应度值(对数尺度)')
plt.legend()
plt.grid(True)
plt.show()
return results
# 运行综合测试
comprehensive_results = comprehensive_function_test()
5.2 工程优化应用
5.2.1 无人机路径规划
蝙蝠算法在无人机三维路径规划中表现出色:
def uav_path_planning():
"""无人机三维路径规划"""
def path_planning_fitness(path):
"""路径规划适应度函数"""
# 路径长度
length = 0
for i in range(len(path) - 1):
length += np.linalg.norm(path[i+1] - path[i])
# 障碍物惩罚
obstacle_penalty = 0
obstacles = [(50, 50, 50), (80, 20, 30), (30, 70, 60)] # 障碍物位置
for point in path:
for obstacle in obstacles:
distance = np.linalg.norm(point - obstacle)
if distance < 10: # 安全距离
obstacle_penalty += (10 - distance) * 100
# 高度惩罚
height_penalty = 0
for point in path:
if point[2] < 20 or point[2] > 100: # 高度限制
height_penalty += abs(point[2] - 60) * 10
return length + obstacle_penalty + height_penalty
# 路径规划参数
dim = 3 # 三维空间
num_waypoints = 10 # 路径点数量
pop_size = 40
max_iter = 200
ba = BatAlgorithm(path_planning_fitness, dim * num_waypoints, pop_size,
lb=[0]*dim*num_waypoints, ub=[100]*dim*num_waypoints, max_iter=max_iter)
best_path, best_fitness, convergence = ba.optimize()
print("无人机路径规划结果:")
print(f"最优路径适应度: {best_fitness:.4f}")
# 可视化路径
if dim == 3:
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# 绘制路径
path_points = best_path.reshape(-1, 3)
ax.plot(path_points[:, 0], path_points[:, 1], path_points[:, 2], 'b-o', linewidth=2)
# 绘制障碍物
obstacles = [(50, 50, 50), (80, 20, 30), (30, 70, 60)]
for obstacle in obstacles:
ax.scatter(obstacle[0], obstacle[1], obstacle[2], c='red', s=100, marker='o')
ax.set_xlabel('X坐标')
ax.set_ylabel('Y坐标')
ax.set_zlabel('高度')
ax.set_title('无人机三维路径规划结果')
plt.show()
return best_path, best_fitness
# 运行路径规划
best_path, best_path_fitness = uav_path_planning()
5.2.2 图像处理应用
蝙蝠算法在图像分割、特征提取等图像处理任务中也有广泛应用:
def image_segmentation_optimization():
"""基于BA的图像分割优化"""
def segmentation_fitness(thresholds):
"""图像分割适应度函数(基于类间方差)"""
if len(thresholds) != 2: # 双阈值分割
return float('inf')
t1, t2 = sorted(thresholds)
# 简化版的Otsu类间方差计算
# 实际应用中需要真实的图像直方图
w0 = t1 / 255
w1 = (t2 - t1) / 255
w2 = (255 - t2) / 255
# 计算类间方差
mean0 = t1 / 2
mean1 = (t1 + t2) / 2
mean2 = (t2 + 255) / 2
global_mean = 127.5
between_class_variance = w0 * (mean0 - global_mean)**2 + \
w1 * (mean1 - global_mean)**2 + \
w2 * (mean2 - global_mean)**2
return -between_class_variance # 最大化类间方差
# 图像分割参数
dim = 2 # 两个阈值
pop_size = 30
max_iter = 100
ba = BatAlgorithm(segmentation_fitness, dim, pop_size, lb=[0, 0], ub=[255, 255], max_iter=max_iter)
best_thresholds, best_variance, _ = ba.optimize()
print("图像分割优化结果:")
print(f"最优阈值: {sorted(best_thresholds)}")
print(f"最大类间方差: {-best_variance:.4f}")
return best_thresholds, best_variance
# 运行图像分割优化
best_thresholds, best_variance = image_segmentation_optimization()
5.2.3 机器学习超参数优化
BA算法可以用于优化机器学习模型的超参数:
from sklearn.model_selection import cross_val_score
from sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
def optimize_svm_with_ba():
"""使用BA算法优化SVM超参数"""
# 加载数据
data = load_iris()
X, y = data.data, data.target
# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
def svm_fitness(params):
"""SVM分类器的适应度函数"""
C = params[0] # 正则化参数
gamma = params[1] # 核函数参数
# 参数范围限制
if C < 0.1 or C > 10 or gamma < 0.01 or gamma > 1:
return float('inf') # 惩罚不可行解
model = SVC(C=C, gamma=gamma, random_state=42)
# 5折交叉验证
scores = cross_val_score(model, X_scaled, y, cv=5, scoring='accuracy')
error_rate = 1 - np.mean(scores)
return error_rate
# 使用BA优化SVM参数
dim = 2
pop_size = 20
max_iter = 50
ba = BatAlgorithm(svm_fitness, dim, pop_size, lb=[0.1, 0.01], ub=[10, 1], max_iter=max_iter)
best_params, best_error, convergence = ba.optimize()
print("SVM参数优化结果:")
print(f"最优C参数: {best_params[0]:.4f}")
print(f"最优gamma参数: {best_params[1]:.4f}")
print(f"最小错误率: {best_error:.4f}")
return best_params, best_error
# 运行SVM参数优化
best_svm_params, best_svm_error = optimize_svm_with_ba()
表3:蝙蝠算法应用领域总结
| 应用领域 | 具体问题 | 算法优势 | 实现难点 |
|---|---|---|---|
| 函数优化 | 多峰函数、高维函数优化 | 全局搜索能力强,收敛速度快 | 参数调优需要经验 |
| 路径规划 | 无人机、机器人导航 | 处理复杂约束条件 | 环境建模复杂性 |
| 图像处理 | 图像分割、特征提取 | 多阈值优化能力 | 需要专业领域知识 |
| 机器学习 | 超参数优化、特征选择 | 自动化调参,提高模型性能 | 计算成本较高 |
| 工程设计 | 参数优化、结构设计 | 处理复杂工程约束 | 约束处理技巧要求高 |
6 总结与展望
6.1 算法优势与局限
蝙蝠算法的优势:
- 原理简单直观:基于蝙蝠回声定位行为,概念清晰,易于理解和实现
- 参数设置相对简单:相比其他智能优化算法,BA需要调节的参数较少
- 收敛性能良好:自适应机制使算法能自动平衡探索与开发
- 全局搜索能力强:频率调节和局部搜索机制使算法具有强大的全局探索能力
- 应用广泛:已在多个领域验证有效性
蝙蝠算法的局限:
- 易陷入局部最优:个体缺乏变异机制,对多峰问题处理能力有限
- 理论分析不足:数学理论基础相对薄弱,收敛性证明不够完善
- 参数敏感性:音量和脉冲率等参数对性能影响较大
- 高维问题挑战:处理超高维复杂问题时,性能可能下降
6.2 未来研究方向
基于当前研究现状,蝙蝠算法的未来发展方向包括:
- 理论分析深化:加强算法的收敛性、复杂度等数学理论分析
- 多目标扩展:开发更高效的多目标优化版本
- 动态环境适应:研究动态环境下的BA算法,提高算法在变化环境中的适应能力
- 混合算法设计:与其他优化算法深度融合,形成性能更优异的混合优化算法
- 大规模优化:改进算法结构,使其更适合处理高维大规模优化问题
- 实际应用拓展:将BA算法应用到更多新兴领域,如深度学习、大数据分析等
6.3 实用建议
对于研究者和工程师,在使用蝙蝠算法时可以考虑以下建议:
- 参数调优:根据问题特性调整种群大小和最大迭代次数,平衡搜索效率与精度
- 算法选择:对于简单问题,标准BA可能已足够;对于复杂问题,可考虑混沌BA或混合BA
- 约束处理:对于约束优化问题,采用合适的约束处理技术(如罚函数法)
- 多次运行:由于算法的随机性,建议多次独立运行并取最优结果
- 性能对比:与其他优化算法进行对比实验,确保选择最适合当前问题的优化方法
蝙蝠算法作为优化算法家族的重要成员,已在多个领域展现出良好的应用前景。随着研究的深入和应用的拓展,BA算法及其改进版本将在解决复杂优化问题中发挥越来越重要的作用。

























 839
839

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










