端到端的图像压缩----《Variational Image Compression With A Scale Hyperprior》论文笔记

论文地址：https://arxiv.org/abs/1802.01436

代码地址：https://github.com/tensorflow/compression

变分自编码器理论介绍（个人认为讲的最详细）：https://www.sohu.com/a/226209674_500659

变分自编码器论文地址：https://arxiv.org/abs/1312.6114

变分自编码器代码地址（非官方）：https://github.com/kvfrans/variational-autoencoder

Balle  google大神，入门必读。该文章仅供本人笔记用，如果问题欢迎讨论。

一 简介

       该模型并入了一个超级优先级，用来捕获特征图之间的空域冗余问题。这种优先的边信息的使用在传统编码中已经通用，但是在自编码器中还未得到开发。且该模型与之前的模型不同，超先验网络结构是与自编码器一起进行端到端的训练优化的。

二 内容

       在以往的图像压缩方法中，用于压缩潜在表示的熵模型通常表示为联合分布，甚至完全分解的分布 $p_{\hat{y}}（\hat{y}）$。注意，我们需要区分潜在表示的的实际边际分布和熵模型对于潜在表示的熵模型分布。虽然通常假设熵模型具有参数化形式，并且参数适合数据，但是边缘是未知的分布，当熵模型估计潜在表示出现值越精准，则其越接近理论熵值。编码器/解码器对使用它们的共享熵模型可以实现的最小平均码长由两个分布之间的香农交叉熵给出：$$R=E_{\hat{y}\sim m}[-lo{g}_2{p}_{\hat{y}}(\hat{y})]$$则当模型的估计分布等于实际的边际分布的时候，此时熵值达到最小。这揭示了当潜在表示的实际分布存在统计依赖的关系的时候，使用完全分解的熵模型将会导致次优（非最优的压缩性能）。

       在常规压缩方法中，该辅助信息的结构是手工设计的。相反，本文中介绍的模型本质上是学习熵模型的潜在表示，就像基础压缩模型学习图像的表示一样。该模型是端到端的优化模型，所以通过学习平衡信息量和预期的熵模型改进，可以使总的预期代码长度最小。这是通过变分自动编码器（VAE），概率生成模型和近似推理模型增强正式表达的方式来完成的。 Ballé（2017）之前曾指出，一些基于自动编码器的压缩方法在形式上等同于VAE，其中如上所述的熵模型对应于潜在表示中的先验模型。在这里，我们使用这种形式主义来表明，可以将边信息视为熵模型参数的先验信息，从而使它们成为潜在表示的先决条件。具体来说，本文扩展了Ballé（2017年）等人提出的模型。它具有先验网络，并具有一个超先验的功能，即表示潜在表示的空间相邻元素在其比例尺上倾向于一起变化。

2.2 数据流程

图1.整体网络框架图

       输入图片经过主编码器 $ga$ 获得了输出 $y$ ，即通过编码器得到的潜在特征表示，经过量化器 $Q$ 后得到输出$\hat{y}$，超先验网络对 $\hat{y}$ 进行尺度（$\sigma$）捕获，对潜在表示每一个点进行均值为0，方差为 $\sigma$ 的高斯建模，不同于以往的方法，以往的方式通过对整体潜在特征进行建模，即一个熵模型在推理阶段应用在所有的特征值熵，而超先验架构为每个特征点都进行了熵模型建模，通过对特征值的熵模型获取特征点的出现情况以用于码率估计和熵编码。

       由于算术/范围编码器在编解码阶段都需要解码点的出现概率或者CDF（累计概率分布）表。故而需要将这部分信息传输到解码端，以用于正确的熵解码。故而超先验网络对这部分信息先压缩成 $z$,通过对 $z$ 进行量化熵编码传输至超先验解码端，通过超先验解码端解码学习潜在表示 $y$ 的建模参数。通过超先验网络获取得到潜在表示 $y$ 的建模分布后，通过对其建模并且对量化后的 $\hat{y}$ 进行熵编码得到压缩后的码流文件，而通过熵解码得到 $\hat{y}$，传统的编解码框架中往往设定反量化模块，而在解码网络中，包含了反量化的功能。故而在反量化模块在论文中并未部署，再将熵解码结果 $\hat{y}$ 输入到主解码端，得到最终的重建图片 $\hat{x}$ 。对于整个网络的参数优化问题，依旧采用整体的率失真函数：$$L=\lambda \cdot D+R$$其中 $D$ 代表重建图像与原图的失真度，$R=R_{\hat{y}}+R_{\hat{z}}$ 代表整体框架的压缩码率。

       上述量化会引入误差，这种误差在有损压缩的情况下是可以容忍的，同时该模型也遵循Balle在2017年论文中的量化方式，采用添加均匀噪声的形式近似量化操作，传统方式通过调整量化步长的形式进行率失真控制，而端到端的优化技术通过对码率和失真的权衡进行控制，如使用上述公式中的 $\lambda$ 进行率失真折衷。

假设熵编码技术有效运行，则可以再次将其写为交叉熵：$$R=E_{x\sim p_x}[-lo{g}_2{p}_{\hat{y}}(Q(g_a(x;{\varphi }_g)))]$$ 其中 $Q$ 表示量化函数，而$p_{\hat{y}}$表示熵模型。在这种情况下，潜在表示的边际分布来自（未知）图像分布$p_x$，$Q$ 量化形式，以及分析变换的属性都会影响最终实际的编码码率值。

2.3 变分自编码器

图2.变分自编码器

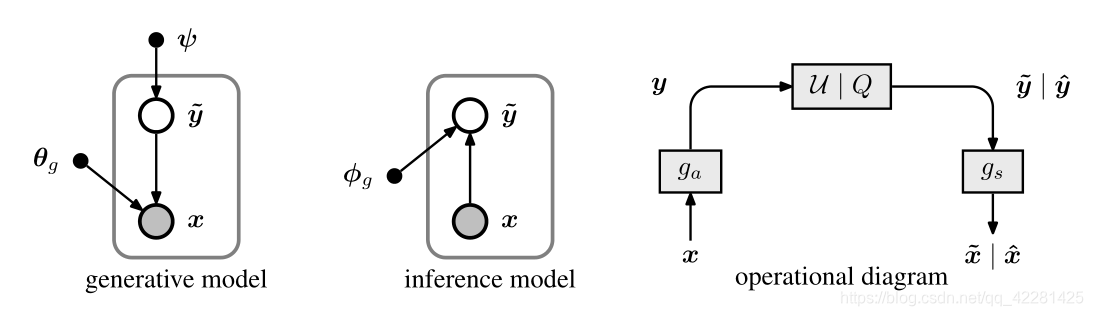
优化问题可以表示为变分自动编码器，也就是说，图像的自编码的编码器和解码器类似于图像的概率生成模型与推理模型（图2）。在变分推论中，目标是通过最小化他们对KL散度的期望（期望后验概率趋向于正太分布，并且保持变分自编码器的生成模式不退化为常规自编码器），以参数变分密度$q(\tilde{y}|x)$ 近似被认为是难解的真实后验$p_{\tilde{y}|x}(\tilde{y}|x)$。在数据分布$p_x$上的差异：$$E_{x\sim p_x}{D}_{KL}[q||p_{\tilde{y}|x}]=E_{x\sim p_x}{E}_{\tilde{y}\sim q}[logq(\tilde{y}|x)-log{p}_{x|\tilde{y}}(x|\tilde{y})-log{p}_{\tilde{y}}(\tilde{y})]+const$$通过将参数密度函数与变换编码框架进行匹配，可以了解到，KL散度的最小化等效于针对率失真性能优化压缩模型。我们在这里已经指出，第一项将评估为零，第二项和第三项分别对应于加权失真和比特率。让我们仔细看看每个术语。首先，“推理”的机制是计算图像的分析变换并添加均匀噪声（作为量化的替代），因此:$$q(\tilde{y}|x,{\varphi }_g)=\prod _{i}U(\widetilde{y_i}|y_i-1/2,y_i+1/2)->with->y=g_a(x;{\varphi }_g)$$其中$U$表示以$y_i$为中心的均匀分布。由于均匀分布的宽度是恒定的（等于1），因此KL散度中的第一项在技术上估计为零，并且可以从损失函数中删除(存疑)。

其中第二项对应了编码框架中的失真度，对于上述公式假定$$p_{x|\tilde{y}}(x|\tilde{y},{\theta }_g)=N(x|\tilde{x},(2\lambda {)}^{-1}1)-->with-->\tilde{x}=g_s(\tilde{y};{\theta }_g)$$表示在参数神经网络中，$\tilde{x}$ 已经由 $\tilde{y}$ 从生成器中运行得到，并且通过率失真进行了 $\lambda$ 的权衡，即KL散度最小时,第二项去除负号使得对数似然模型最大化：$log{p}_{x|\tilde{y}}(x|\tilde{x})$，等价于 $\tilde{y}$ 通过解码器的重构图与原始图片的失真最小化，直接理解可以解释为：根据解码得到的像素点 $\tilde{x}$ 推测 $x$ 的后验概率，当两者像素值越接近的时候，其得到的后验概率越大，则 $-log{p}_{x|\tilde{y}}(x|\tilde{x})$ 的计算值（即自信息）越小。因此等价于图像编码中的失真项。

第三项更便于理解，$-log{p}_{\tilde{y}}(\tilde{y})$ 在信息论中即表示 $\tilde{y}$ 的自信息，其对应了编码框架中的码率估计模型或者说由熵编码后待编码点的码率大小。
      

2.4 思路介绍

图2.潜在表示可视化图，最左边是原图，中左是得到的潜在表示（选取熵率最大的那一张） $y$，中右表示通过超先验网络捕获到的尺度信息即（ $\sigma$）的特征图，最右边则是归一化之后的，通过 $y/\sigma$得到的，可以看出除以 $\sigma$之后，消除了空间结构冗余。

根据上图可以看出，对于编码器的结果 $y$ 存在结构冗余，房子的结构上依旧保留了下来，并且可以看出，捕获的 $\sigma$在结构上与未消除的结构冗余是一致的，对一组目标变量之间的依存关系进行建模的标准方法是引入隐含变量，条件是假定目标变量是独立的（Bishop，1999）。我们引入了一组额外的随机变量 $\sigma$来捕获空间相关性,假定通过 $\sigma$ 消除后的变量为独立标准正太分布模型。$$p_{\tilde{y}|\tilde{z}}(\tilde{y}|\tilde{z},{\theta }_h)=\prod _i(N(0,{\tilde{\sigma }}_i^2)\ast U(-1/2,1/2))(\widetilde{y_i})$$对应的意思是 ${\prod }_i(N(0,{\tilde{\sigma }}_i^2)\ast U(-1/2,1/2))$ 为 $\widetilde{y_i}$ 的概率密度函数，其中 $p_{\tilde{y}|\tilde{z}}(\tilde{y}|\tilde{z},{\theta }_h)$ 表示某个 $y_i$ 在被先验认知为正太分布，即确认了 $\tilde{z}$ 和超参数 $\theta$的情况下，得到的正太分布的方差值，在训练阶段的量化为均匀噪声，通过卷积形式松弛概率密度（概率密度函数图形更加平缓）。 个人以为公式最后的$({\tilde{y}}_i)$是不是可以删除？

同理对于公式$$p_{\tilde{z}|\psi }(\tilde{z}|\psi )=\prod _i(p_{z_i|{\psi }^i}({\psi }^{(i)})\ast U(-1/2,1/2)(\widetilde{z_i})$$其中${\prod }_i(p_{z_i|{\psi }^i}({\psi }^{(i)})$这部分为$FactoredEntropymodel$通过离线学习得到的概率密度函数，通过对所有的点离线建模，统一认为所有的点服从上述的概率密度函数，同理 $U(-1/2,1/2)$ 的卷积运算表示量化过程的均匀噪声的添加，对概率密度具有松弛作用，不利于准确的码率估计，但是量化操作对于熵编码降低码率是必要的。最后的$({\tilde{z}}_i)$也能删除吧？

全文思路建立在编码器提取潜在特征的特征存在一定的结构冗余，这部分结构冗余即一些像素点存在相关性，本文的思路即如何消除这部分的相关性呢？

• 首先通过超先验网络对潜在特征点进行结构层次的信息捕获，通过超先验感知潜在点的结构信息，原始的方式是基于统计的方式，不是内容自适应，无法识别结构信息。
• 对潜在特征点进行自适应建模，由于算数编码的性质，在编码某一像素点，其概率值估计地越精准，则编码效率越高，而捕获这种结构实质的作用是通过 $\sigma$ 参数告诉熵编码器，这个位置根据捕获到地结构，其概率在原来统计熵模型的情况下是没办法捕获这种结构通过对源模型进行高斯分布，通过方差参数捕获到的结构对概率进行调整。
• 这种熵模型是可以改动的，因为实际中真正的概率不一定符合高斯模型，目前最新的是高斯混合模型。其中

三 核心代码

3.1 整体流程

  y = analysis_transform(x)  //编码器
  z = hyper_analysis_transform(abs(y)) //超先验编码获得z
  z_tilde, z_likelihoods = entropy_bottleneck(z, training=True)  //对z进行量化，以及码率估计
  sigma = hyper_synthesis_transform(z_tilde) //解码z，得到对应的sigma 参数，即方差
  scale_table = np.exp(np.linspace(
      np.log(SCALES_MIN), np.log(SCALES_MAX), SCALES_LEVELS)) //构建分组边界
  conditional_bottleneck = tfc.GaussianConditional(sigma, scale_table) //实例化高斯分布的熵率模型
  y_tilde, y_likelihoods = conditional_bottleneck(y, training=True) //量化y，以及估计y的码率
  x_tilde = synthesis_transform(y_tilde) //根据量化后的值，重构图像

不赘述四个编码器的代码，就是卷积层以及GDN层的叠加，核心在于介绍$GaussianConditional这个模块$，该模块训练过程返回两个数值，量化以及每个待编码值的出现概率的估计。

3.2

outputs = self._quantize(inputs, "noise" if training else "dequantize") //对输入进行量化
likelihood = self._likelihood(outputs) //对量化后的数值进行熵率估计。
  
'''训练过程进行添加（-0.5，0.5）的均匀噪声，推理过程则四舍五入。'''
def _quantize(self, inputs, mode):
    # Add noise or quantize (and optionally dequantize in one step).
    half = tf.constant(.5, dtype=self.dtype)
    _, _, _, input_slices = self._get_input_dims()

    if mode == "noise":
      noise = tf.random.uniform(tf.shape(inputs), -half, half)
      return tf.math.add_n([inputs, noise])

    medians = self._medians[input_slices]
    outputs = tf.math.floor(inputs + (half - medians))

    if mode == "dequantize":
      outputs = tf.cast(outputs, self.dtype)
      return outputs + medians
    else:
      assert mode == "symbols", mode
      outputs = tf.cast(outputs, tf.int32)
      return outputs

def _likelihood(self, inputs):
    lower = self._logits_cumulative(inputs - half, stop_gradient=False) //获取分布函数的下界
    upper = self._logits_cumulative(inputs + half, stop_gradient=False) //获取分布函数的上界
    # Flip signs if we can move more towards the left tail of the sigmoid.
    sign = -tf.math.sign(tf.math.add_n([lower, upper]))
    sign = tf.stop_gradient(sign)
    likelihood = abs(tf.math.sigmoid(sign * upper) - tf.math.sigmoid(sign * lower)) //上界减去下界后即可得到估计的概率值。
    return likelihood

在假设 $y$ 服从均值为0，方差为 $\sigma$ 的正太分布后，可以根据这一点对logits_cumulative 进行重构，可以直接根据已知方差参数的正太概率密度函数进行上下界的分布函数求解得到出现的概率情况。替换上述$logits-cumulative$ 为下面的 $standardized-cumulative$

  def _likelihood(self, inputs):
    values = inputs
    # This assumes that the standardized cumulative has the property
    # 1 - c(x) = c(-x), which means we can compute differences equivalently in
    # the left or right tail of the cumulative. The point is to only compute
    # differences in the left tail. This increases numerical stability: c(x) is
    # 1 for large x, 0 for small x. Subtracting two numbers close to 0 can be
    # done with much higher precision than subtracting two numbers close to 1.
    values = abs(values)
    upper = self._standardized_cumulative((.5 - values) / self.scale)
    lower = self._standardized_cumulative((-.5 - values) / self.scale)
    likelihood = upper - lower
    return likelihood

  def _standardized_cumulative(self, inputs):
    half = tf.constant(.5, dtype=self.dtype)
    const = tf.constant(-(2 ** -0.5), dtype=self.dtype)
    # Using the complementary error function maximizes numerical precision.
    return half * tf.math.erfc(const * inputs)

四 性能结论

性能上相较于BPG（HEVC帧内编码）差了一点，但是相比于原始的2017年的论文的优化上，在R-D性能上，同码率下提高了一点几个db,可以说奠定了大部分图像压缩研究的基础。总之两个字，牛X。