初学者对于SVM的一点点学习心得

详解SVM

SVM是由Vapnik和同事于1992年提出的一种分类算法。由于其优异的分类性能以及在解决线性和非线性问题中都具有的优秀效果，一经提出，就受到广泛欢迎，甚至作为机器学习领域的经典算法之一。作者在刚开始接触SVM时也是一头雾水，特别是看了很多推导SVM的博客，感觉都有点似懂非懂，不久前有幸在b站上观看了清华大学袁博老师的数据挖掘课程，被袁博老师深入浅出的讲解深深折服。至此，作者对SVM才有了一定程度上的了解，因此，在本篇文章中，作者把对SVM的学习心得整理为了一篇博客，与大家分享。本文将按照SVM的整个发展历程对SVM进行简单推导，整个推导过程深深受到了袁博老师的影响（附：清华大学袁博老师的《数据挖掘》课程链接）。

SVM的发展历程

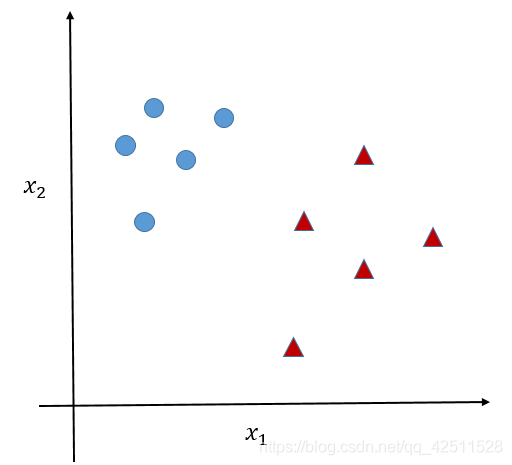
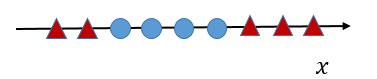
SVM作为机器学习领域的经典算法之一，相信很多同学都听过它的大名。其优异的分类性能使之成为工业界应用范围最广的聚类算法之一。但SVm这座宏伟的大楼不是一蹴而就的，其可以追溯到上个世纪60年代，当时就是作为最简单的线性分类器提出来的，目的也非常纯粹，就是为了解决最简单的线性分类问题，如下图所示，我们希望训练出一个超平面将蓝色点和红色点分开。

在解决了这个问题之后，人们发现实际中很多问题不是像上图那样理想，蓝色点和红色点泾渭分明，很容易被分开。实际上，在很多情况下，由于噪声的存在，

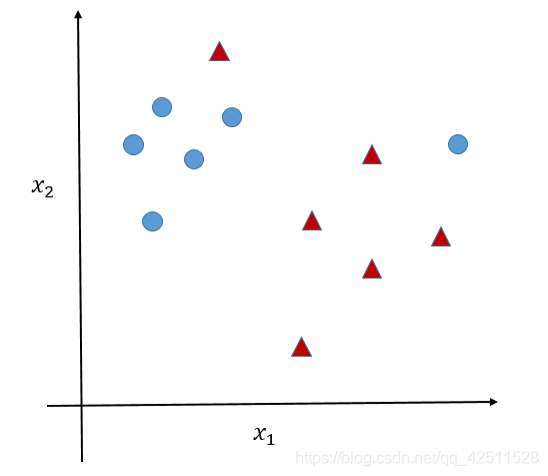
如图所示，有个别离群点混入了相对的点集团中，导致之前的Linear Classifier找不到合适的超平面进行分割，此时就产生了进阶版SVM–具有Soft Margin的SVM。

研究到这里，SVM已经彻底解决了线性分类问题。但相对于线性分类问题，非线性分类问题才是实际中最为常见的问题，我们举一个简单的例子，

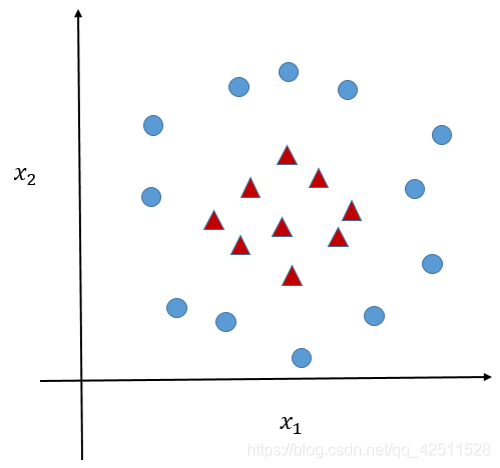
很明显可以看出，无论用何种超平面，都无法正确分割上图中的红点和蓝点。因此较真的科学家们就开始尝试改进SVM来解决非线性分类问题，然而，没想到幸运的是，真的有人研究出了可以用于解决非线性分类的改进版SVM–基于kernel核函数的SVM。这位大牛便是我们一开始就提到过的Vapnik。

但后面我们要讲到，如果强行用核函数的话，很可能由于计算复杂度太高，导致问题的难度噌噌噌往上涨（就和练功一个道理，如果练功用力过度，很容易急火攻心、走火入魔，甚至香消玉殒）。所以最后一部分，我们就讲一个小小的Kernel Trick，通过这个小trick，解决SVM就如同探囊取物一般简单。

Linear Classifier

在构建Linear Classifier之前，我们需要先搞明白理想的分类器是什么样子？

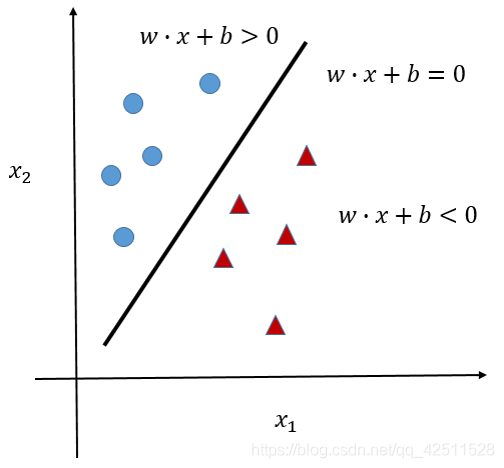
如上图所示，假如我们产生了一个超平面$w\cdot x+b=0$，则如何能区分蓝色点和红色点呢？学过初等数学的话，就会知道当一条直线为$w\cdot x+b=0$时，这条直线的一侧必然是$w\cdot x+b>0$，另一侧必然是$w\cdot x+b<0$。那我们将直线换成超平面也是一样的，且基于超平面的这个特点，我们可以得到分类器的核心公式：
$$\begin{array}{rl}f(x,w,b)& =sign(g(x))\\ & =sign(w\cdot x+b)\end{array}$$
其中，$sign()$是符号函数，如图所示。

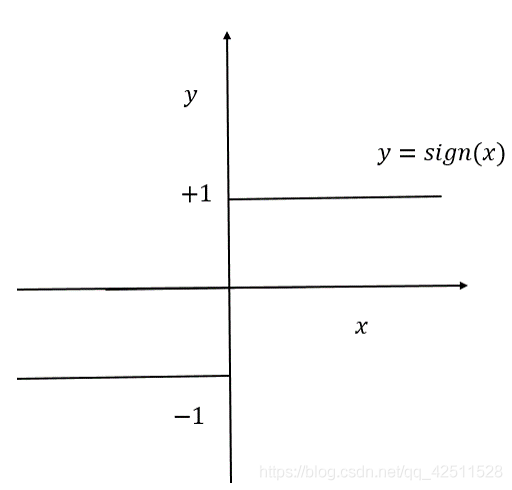
这里，我们认为设定蓝色点的$label=+1$，红色点的$label=-1$。通过这个分类器的核心公式，我们就可以将蓝色点和红色点完美地区分开来。因此下面的所有内容都是关于如何构建这个$g(x)=w\cdot x+b$，也即如何设定一对合适的参数$w$和$b$。

在思考$w$和$b$之前，我们先熟悉一个知识点，点到超平面的距离如何计算？如下图所示。

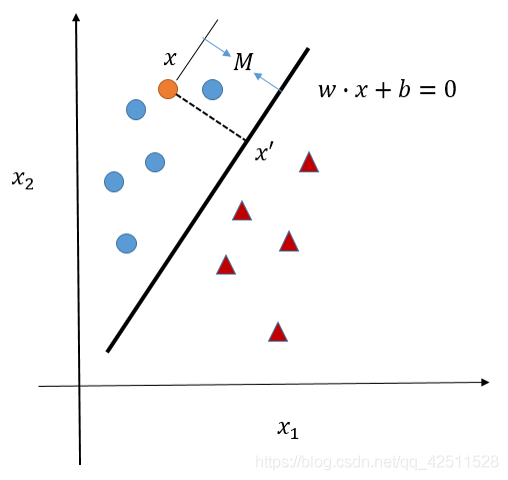
这里，我们设$x$到超平面$w\cdot x+b=0$的距离为$M$。则，根据点到（超平面）直线的距离公式，
$$M=||x-x^{\prime }||=\frac{|g(x)|}{||w||}$$
其中，当$x=(0,0)（原点）$时，$M=\frac{|g(0,0)|}{||w||}$。

知道了这个距离公式后，我们就可以接着思考构建合适超平面的问题了。我们要思考的第一个问题便是，如下图所示，可以用于正确分类红点和蓝点的超平面有很多，那么哪一个超平面是我们需要的最佳超平面呢？

在这个问题的基础上，我们就引出了Margin的概念。我们定义Margin为分类的超平面和对应类别最近的样本点之间的距离，如图所示。

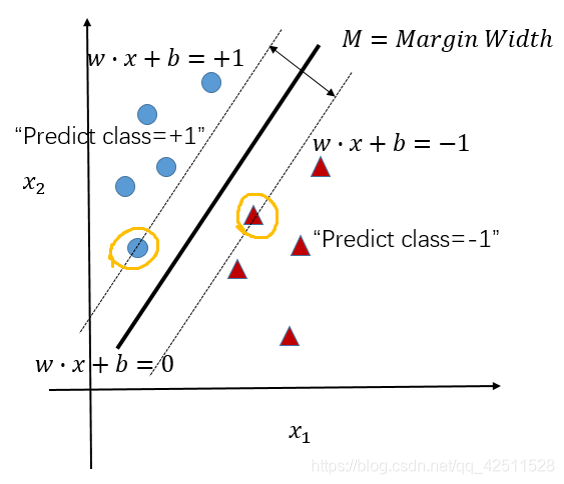
我们这里认为规定M=Margin Width，很明显可以看到，不同的超平面对应的Margin Width并不相同。虽然每一种超平面都实现了对已有数据点的完美分割，但我们不知道当前超平面对未知数据点的分类效果。因此，为了保证最佳分类效果，我们选择Margin Width最大的超平面作为最优超平面，用数学公式表达为：
$$maxM$$
因此，我们又将问题转化为了如何表达$M$。为了表达$M$，我们这里又人为规定一下，如上图所示，Margin的两个边界分别为$w\cdot x+b=+1$和$w\cdot x+b=-1$，至于为什么这么规定？因为无论$w\cdot x+b=$多少，都与最终结果无关，大家也可以尝试一下，比如：$w\cdot x+b=0.5$等等。通过设置$w\cdot x+b=+1$和$w\cdot x+b=-1$这两条边界，我们也就规定了这些数据点中，大于等于$+1$的数据点为蓝点，小于等于$-1$的点为红点，超平面为$w\cdot x+b=0$。

到这里，我们就可以发现，超平面的确定只与两条边界有关，换句话说，只与边界上的数据点有关（如上图，我用黄线圈了起来）。至于其它数据点如何分布，本质上与超平面没什么关系。因此，边界上的点才是关键点，我们将这些点称之为支持向量。可以想象，即使我们有上千万的数据点，但真正构成支持向量的点可能只有几十个。如果能将这几十个点找到，问题的计算复杂度将大大降低。

假如$w\cdot x+b=+1$上有一点$x^{+1}$，则该点到超平面的距离为$M_{x^{+}}=\frac{|g(x^{+})|}{||w||}$；$w\cdot x+b=+1$上有一点$x^{+1}$时，同理。因此，$M=\frac{2}{||w||}$。我们的目标便是$max\frac{2}{||w||}$。

但在$max\frac{2}{||w||}$的同时，我们还需要保证超平面成功分类，因此必须要保证：
$$\begin{gathered} w\cdot x_i+b\ge 1,if{y}_i=+1 \\ w\cdot x_i+b\le -1,if{y}_i=-1 \end{gathered}$$
将这两个式子合并一下，就可以得到：
$$y_i\ast (w\cdot x_i+b)-1\ge 0$$

最终，我们就可以得到，一个完整的优化目标，
$$\begin{array}{r}maxM=\frac{2}{||w||}\\ s.t.y_i\ast (w\cdot x_i+b)-1\ge 0\end{array}$$

Linear SVM

上节讲到，SVM分类器的核心问题归根结底就是解决下面的这个二次优化问题。
$$\begin{array}{r}maxM=\frac{2}{||w||}\\ s.t.y_i\ast (w\cdot x_i+b)-1\ge 0\end{array}$$
但这个不是一般求解优化问题的标准形式，因此，我们将这个式子稍稍变一下，变为标准形式：
$$\begin{array}{r}minM=\frac{1}{2}{w}^{T}w\\ s.t.y_i\ast (w\cdot x_i+b)-1\ge 0\end{array}$$
注意，这里将$||w||$变为$w^{T}w$是为了计算方便，不会影响后面的结果。

因此，本节中，作者就带领大家一起尝试求解这个优化问题。既然这个是含限制条件的优化问题，那我们就自然而然要想到Lagrange乘子法（忘了的同学可以自行百度，重新学习一下）。当然，要注意一下，我们在高等数学中学过的lagrange乘子法是用于等式约束的，而这里是不等式约束，会有一点小小的不同，我们后面会讲到。这里我们继续，采用lagrange乘子法的结果是
$$L_p=\frac{1}{2}||w|{|}^2-\sum _{i=1}^l{\alpha }_i{y}_i(w{x}_i+b)+\sum _{i=1}^l{\alpha }_i\text{\hspace{1em}(1)}$$

既然是用lagrange乘子法，那就必然要对每一个变量进行求导，
$$f(x)=\{\begin{array}{rl}& \frac{\partial L_p}{\partial w}=0\Rightarrow w=\sum _{i=1}^l{\alpha }_i{y}_i{x}_i\\ & \frac{\partial L_p}{\partial b}=0\Rightarrow \sum _{i=1}^l{\alpha }_i{y}_i=0\end{array}\text{\hspace{1em}(2)}$$
然后，再将(2)式代回(1)式中，就可以得到下面这个式子，
$$\begin{array}{rl}{L}_D& =\sum _{i=1}^l{\alpha }_i-\frac{1}{2}\sum _{i,j}^l{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i{x}_j\\ & =\sum _{i=1}^l{\alpha }_i-\frac{1}{2}{\alpha }^{T}H\alpha \\ s.t.& \sum _{i=1}^l{\alpha }_i{y}_i=0,{\alpha }_i\ge 0\end{array}\text{\hspace{1em}(3)}$$
其中， $H_{ij}=y_i{y}_j{x}_i{x}_j$，注意这里${\alpha }_i\ge 0$就是由于lagrange乘子法的不等式约束产生的。

这里(3)与(1)是对偶问题。再一般情况下，对偶问题是不等价的，但在SVM的情况下，这个对偶问题满足了KKT条件，就等价了（至于什么是KKT条件，感兴趣的同学可以自行百度）。因而，我们就可以转而研究$L_D$了。

$L_D$是一个只和$\alpha$有关的二次优化问题，优化方法有很多，最流行的是SMO算法，有兴趣的同学可以自己看看。在求解$L_D$后，就会得到很多$\alpha$的值。这里要注意，很多$\alpha$都等于0，只有一小部分$\alpha >0$，我们就把非0的$\alpha$对应的点称为support vector。

Soft Margin

在上一节中，我们已经成功求解了SVM问题，但由于在实际中存在大量噪声，如图所示。

因此，不存在超平面能将二者完全分离。此时，我们就要将SVM的表达式稍稍做一些修改，加入Soft Margin，如下图所示。

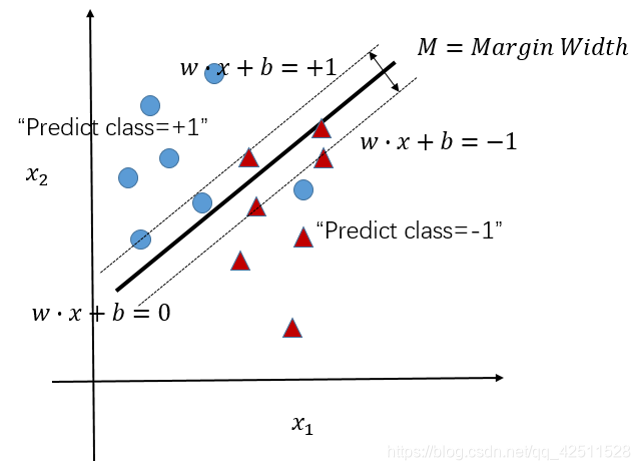
所谓Soft Margin，是指放宽约束条件。原来的约束条件是$y_i\ast (w\cdot x_i+b)-1\ge 0$，我们将其放宽为$y_i\ast (w\cdot x_i+b)-1+{\xi }_i\ge 0$，其中${\xi }_i\ge 0$。之前的约束条件的意思是保证所有数据点都在2个Margin（$wx+b=+1$和$wx+b=-1$）之外，而今，由于噪声的影响，我们将约束条件拓宽为允许有少量数据点位于2个Margin内，甚至极少数点可以越过$wx+b=0$这个超平面。同时将优化目标$\Phi (w)=\frac{1}{2}{w}^{T}w$修改为$\Phi (w)=\frac{1}{2}{w}^{T}w+C\cdot {\sum }_{i=0}^l{\xi }_i$，其中，$C\cdot {\sum }_{i=1}^l{\xi }_i$作为惩罚项，通过设置较大的$C$值，使得${\xi }_i$不要过大。至此，优化函数就修改为了
$$\begin{array}{rl}& min\Phi (w)=\frac{1}{2}{w}^{T}w+C\cdot \sum _{i=0}^l{\xi }_i\\ & s.t.y_i\ast (w\cdot x_i+b)-1+{\xi }_i\ge 0\end{array}$$
和上一节类似，我们还是采用Lagrange乘子法，可以得到
$$L_P=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^l{\xi }_i-\sum _{i=1}^l{\alpha }_i[y_i(w{x}_i+b)-1+{\xi }_i]-\sum _{i=1}^l{\mu }_i{\xi }_i\text{\hspace{1em}(4)}$$

经过求导，就可以得到
$$f(x)=\{\begin{array}{rl}& \frac{\partial L_p}{\partial w}=0\Rightarrow w=\sum _{i=1}^l{\alpha }_i{y}_i{x}_i\\ & \frac{\partial L_p}{\partial b}=0\Rightarrow \sum _{i=1}^l{\alpha }_i{y}_i=0\\ & \frac{\partial L_p}{\partial {\xi }_i}=0\Rightarrow C={\alpha }_i+{\mu }_i\end{array}\text{\hspace{1em}(5)}$$
将(5)代入(4)式，就可以得到
$$\begin{array}{rl}& L_D=\sum _{i=1}^l{\alpha }_i-\frac{1}{2}{\alpha }^{T}H\alpha \\ & s.t.0\le {\alpha }_i\le C,\sum _{i=1}^l{\alpha }_i{y}_i=0\end{array}\text{\hspace{1em}(6)}$$
可以发现，(6)与(3)式非常相似，只多了一个参数C，这个参数在写程序时需要我们手动设置。要求解$L_D$问题，还是用我们提过的SMO算法就可以。

Kernel函数解决Nonlinear Classifier问题

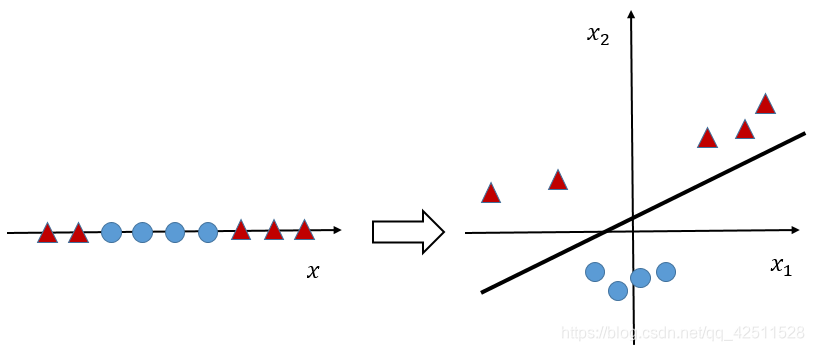
之前我们求解得到的SVM完美解决了线性分类问题，但生活中大量存在线性不可分问题或非线性问题，如下图所示。

左右两张图就是非线性分类的典型例子。我们先讲讲左图，左图是一维数据点分布。很明显，我们无法用一个超平面将这对数据点分为两类。那我们又非常希望解决这个问题，该怎么办呢？科学家们想到了一个非常巧妙的方法–升维，即我们自定义一个函数，将1维投影到2维，投影结果如下图所示：

如果我们能制定一个合适的投影规则，将1维投影到2维后是不是很容易区分。上面那幅右图也是同理，蓝点和红点的分界面是一个$x_1^2+x_2^2=r^2$的圆，不是我们想要的超平面的样子，我们就指定一个规则，将其做个简单的映射$x\to \Phi (x)$，这里$\Phi (x)=x^2$（当然，这里没有升维），就可以得到下图：

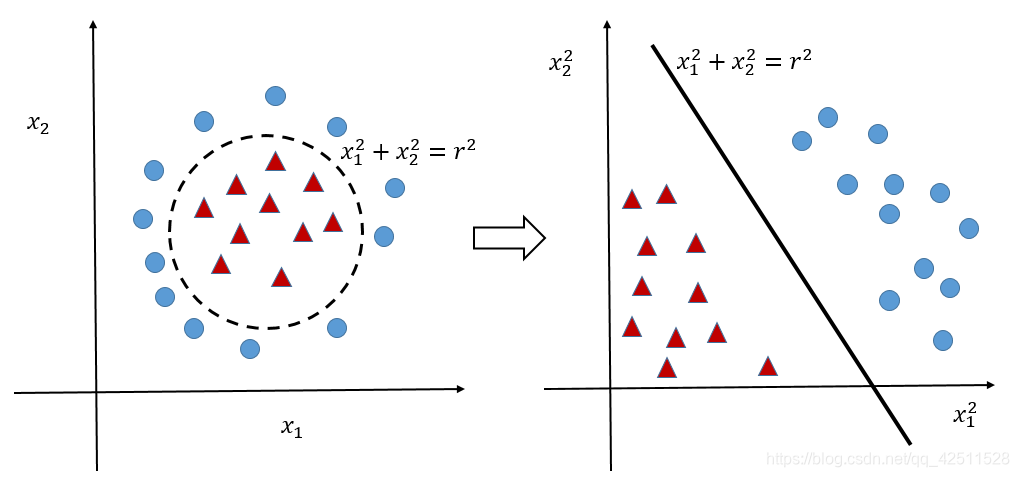
很明显，经过一个简单的映射，就可以将非线性问题转化为线性问题，从而实现分类。这里，我们介绍几种固定的映射方法，例如：
$$\Phi (x)=[1,\sqrt{2}{x}_1,\sqrt{2}{x}_2,...,\sqrt{2}{x}_m,x_1^2,x_2^2,...,x_m^2,\sqrt{2}{x}_1{x}_2,\sqrt{2}{x}_1{x}_3,...,\sqrt{2}{x}_1{x}_m,\sqrt{2}{x}_2{x}_3,...,\sqrt{2}{x}_2{x}_m,...,\sqrt{2}{x}_{m-1}{x}_m{]}^T$$
这个映射关系被称为Quadratic Basis Functions，由常数项、一次项、纯二次项和二次交叉项组成。就好比，原问题只有$[x_1,x_2,...,x_m{]}^T$，$m$项，即$m$维空间，但经过这个映射关系，变成了$C_{m+2}^2=\frac{(m+2)(m+1)}{2}$维空间，约等于$\frac{m^2}{2}$维空间。其实上面那个$\Phi (x)=x^2$的映射就可以视为Quadratic Basis Functiona的特例，只不过由于上图那个问题的特殊性，我们将常数项、一次项、二次交叉项全部省略为0了。

而且，这个Quadratic Basis Functions有一个很好的性质：
当
$$\Phi (a)=[1,\sqrt{2}{a}_1,\sqrt{2}{a}_2,...,\sqrt{2}{a}_m,a_1^2,a_2^2,...,a_m^2,\sqrt{2}{a}_1{a}_2,\sqrt{2}{a}_1{a}_3,...,\sqrt{2}{a}_1{a}_m,\sqrt{2}{a}_2{a}_3,...,\sqrt{2}{a}_2{a}_m,...,\sqrt{2}{a}_{m-1}{a}_m{]}^T$$
和
$$\Phi (b)=[1,\sqrt{2}{b}_1,\sqrt{2}{b}_2,...,\sqrt{2}{b}_m,b_1^2,b_2^2,...,b_m^2,\sqrt{2}{b}_1{b}_2,\sqrt{2}{b}_1{b}_3,...,\sqrt{2}{b}_1{b}_m,\sqrt{2}{b}_2{b}_3,...,\sqrt{2}{b}_2{b}_m,...,\sqrt{2}{b}_{m-1}{b}_m{]}^T$$
时，
$$\Phi (a)\cdot \Phi (b)=1+\sum _{i=1}^{m}2a_i{b}_i+\sum _{i=1}^m{a}_i^2{b}_i^2+\sum _{i=1}^{m-1}\sum _{j=i+1}^{m}2a_i{a}_j{b}_i{b}_j$$
注意，这里$\Phi (a)\cdot \Phi (b)$是对应项相乘求和，比如：$1\cdot 1=1、\sqrt{2}{a}_1\cdot \sqrt{2}{b}_1+\sqrt{2}{a}_2\cdot \sqrt{2}{b}_2+...\sqrt{2}{a}_m\cdot \sqrt{2}{b}_m={\sum }_{i=1}^{m}2a_i{b}_i$等等。

与此对应，可以很惊喜地发现，
$$\begin{array}{rl}(a\cdot b+1{)}^2& =(a\cdot b{)}^2+2a\cdot b+1\\ & =(\sum _{i=1}^m{a}_i{b}_i{)}^2+2\sum _{i=1}^m{a}_i{b}_i+1\\ & =...\\ & =1+\sum _{i=1}^{m}2a_i{b}_i+\sum _{i=1}^m{a}_i^2{b}_i^2+\sum _{i=1}^{m-1}\sum _{j=i+1}^{m}2a_i{a}_j{b}_i{b}_j\end{array}$$
可以得到， $(a\cdot b+1{)}^2=\Phi (a)+\Phi (b)$，Amazing吧！大家可能不知道这意味着什么？因为我们之后利用SVM将低维投射到高维时，经常需要计算$\Phi (a)\cdot \Phi (b)$，但是在$\frac{m^2}{2}$维空间的计算复杂度是$O(m^2)$（因为要分别对$\frac{m^2}{2}$项做乘法运算，数量级是$m^2$，就把$\frac{1}{2}$省略了），计算复杂度非常高。但现在，我们就可以直接在$m$维空间中做$a\cdot b$，再加1和平方，计算复杂度就只有$O(m)$，被大大减小。

换句话说，我们就是在没增加计算复杂度的情况下实现了非线性分类。

Kernel Trick

上一节主要讲了如何解决非线性分类问题，提出了向高维投影的思想，并发现借助数学变换，可以用较低的计算复杂度实现高维向量的计算。那这个向高维映射和我们的SVM有什么关系呢？再回到我们推导的SVM的结果，分类器的表达式为$g(x)=wx+b$，其中，$w={\sum }_{i=1}^l{\alpha }_i{y}_i{x}_i$，$b=\frac{1}{N_s}{\sum }_{s\in S}(y_s-{\sum }_{m\in S}{\alpha }_m{y}_m{x}_m{x}_s)$（$b$的计算就是利用了$b=y-wx$，只不过是把$S$个点都计算了一遍，求了个均值）。但是这里计算出来的$wx+b=0$只适用于线性分类器，要做到解决非线性问题的话，就要用到上节讲过的升维了。

具体做法就是$x_i{x}_j\Rightarrow \Phi (x_i)\Phi (x_j)$，即$w={\sum }_{i=1}^l{\alpha }_i{y}_i\Phi (x_i)$，$b=\frac{1}{N_s}{\sum }_{s\in S}(y_s-{\sum }_{m\in S}{\alpha }_m{y}_m\Phi (x_m)\Phi (x_s)$，对应的分类器就为
$$\begin{array}{rl}g(x)& =wx+b\\ & =\sum _{i=1}^l{\alpha }_i{y}_i\Phi (x_i)\Phi (x)+\frac{1}{N_s}\sum _{s\in S}(y_s-\sum _{m\in S}{\alpha }_m{y}_m\Phi (x_m)\Phi (x_s)\end{array}$$
只不过还是我们之前说过的问题，直接计算$\Phi (x)$的复杂度太高，而$\Phi (x_i)\Phi (x_j)$可用$x_i{x}_j$进行计算。因此，我们以后都是直接计算$K(x_i,x_j)=\Phi (x_i)\Phi (x_j)$，不再单独计算$\Phi (x)$（这里，$K()$就是核函数的意思）。

因此，我们最终得到的非线性分类器就是
$$g(x)=\sum _{i=1}^l{\alpha }_i{y}_{i}K(x_i,x)+\frac{1}{N_s}\sum _{s\in S}(y_s-\sum _{m\in S}{\alpha }_m{y}_{m}K(x_m,x_s))$$
这便是我们想要的结果。

附录

1、几种常见的核函数：
Polynomial: $K(x_i,x_j)=(x_i\cdot x_j+1{)}^d$也就是我们之前提过的个Quadratic Basis Functions，可以将m维映射到$\frac{m^2}{2}$维空间。
Gaussian: $K(x_i,x_j)=exp(-\frac{||x_i-x_j|{|}^2}{2{\sigma }^2})$，映射到无穷维空间（最常用的核函数）。
Hyperbolic Tangent: $K(x_i,x_j)=tanh(k{x}_i{x}_j+c)$，映射到多少维（我不清楚，感兴趣的话，自己查一下）。
2、问题：是不是所有线性不可分问题映射到高维空间中都可以解决？
答：是的。因为有一个指标，叫“VC dimension”。其是用来描述模型的能力指数。如果说存在h个点，这h个点无论怎么被打标签，模型M都可以将其成功分开，则模型M的VBC dimension = h。

什么意思呢？n维空间的超平面的h值=n+1,比如：2维空间的超平面的h=3，即在2维空间中，如果有3个点，无论这3个点怎么摆放，都可以被一个超平面分开，如下图所示。

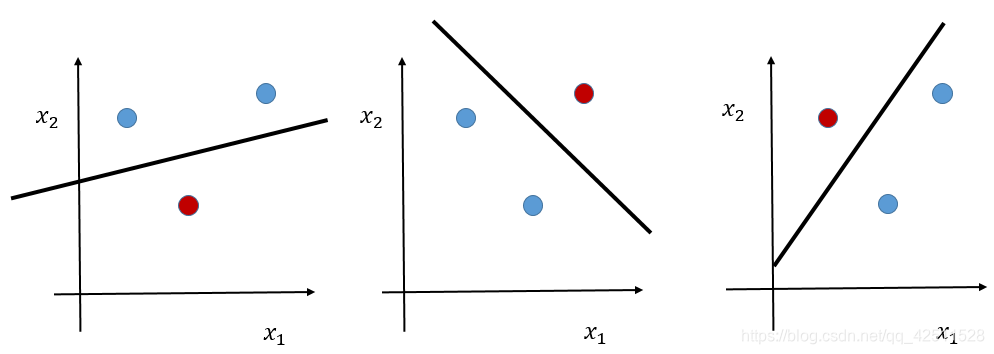
因此，无论有多少个点，就好比有50万个数据点，我们将其升到至少50万-1维空间，就一定可以存在一个超平面将这50万的数据点完美二分类，当然这里说的是最保守的估计（即所有数据点毫无规律，非常难分）。

这里就是简单讲一下VC dimension的概念，如果想了解的更多，可以自行百度。