前言
我们能够知道,一旦旋转已知,那么平移和比例因子也很容易得到。问题的难点在于如何解出旋转。已知三个非共线的点,我们可以很容易地在左边和右边的坐标系中构造一个有用的三角(图2)。把第一个点作为原点,连接第一个点和第二个点,并把该方向作为新x轴的方向。在这三个点构成的平面上,将新的y轴与新的x轴成直角。然后使用右手规则,画出与x,y轴都正交的新z轴。在左右坐标系中都进行这种构造。将这些构造的三角中的一个转化为另一个三角的旋转也是将两个基本的笛卡尔坐标系统联系起来的旋转。这个旋转很容易得到,我们将在下面详细说明。
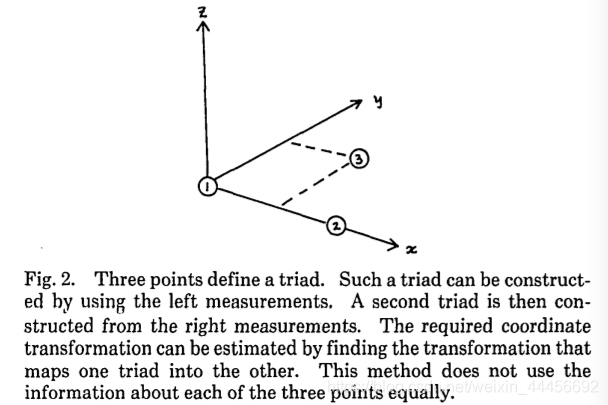
求解思路
让我们把三个点在两个坐标系的中坐标分别记作 r l 1 , r l 2 , r l 3 r_{l1},r_{l2},r_{l3} rl1,rl2,rl3和 r r 1 , r r 2 , r r 3 r_{r1},r_{r2},r_{r3} rr1,rr2,rr3。则:
x 1 = r l 2 − r l 1 x_{1}=r_{l2}-r_{l1} x1=rl2−rl1
然后
x ^ 1 = x 1 ∣ ∣ x 1 ∣ ∣ \hat{x}_{1}=\frac{x_{1}}{||x_{1}||} x^1=∣∣x1∣∣x1
是在左坐标系中新x轴方向上的单位向量。然后设
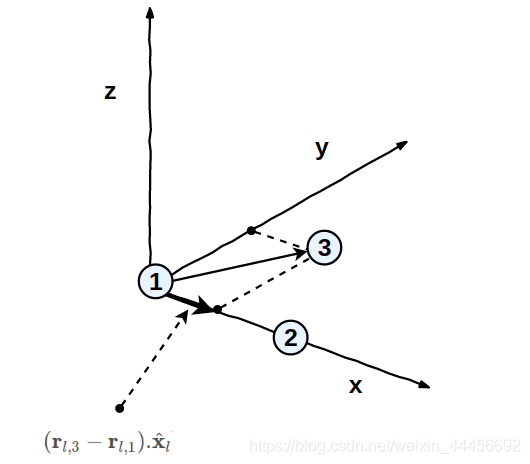
y 1 = ( r l 3 − r l 1 ) − [ ( r l 3 − r l 1 ) ⋅ x ^ 1 ] x ^ 1 y_{1}=(r_{l3}-r_{l1})-[(r_{l3}-r_{l1})\cdot\hat{x}_{1}]\hat{x}_{1} y1=(rl3−rl1)−[(rl3−rl1)⋅x^1]x^1
- [ ( r l 3 − r l 1 ) ⋅ x ^ 1 ] [(r_{l3}-r_{l1})\cdot\hat{x}_{1}] [(rl3−rl1)⋅x^1]表示 [ ( r l 3 − r l 1 ) [(r_{l3}-r_{l1}) [(rl3−rl1)在 x ^ \hat{x} x^上的投影(两向量点乘,得到结果为标量)。 [ ( r l 3 − r l 1 ) ⋅ x ^ 1 ] [(r_{l3}-r_{l1})\cdot\hat{x}_{1}] [(rl3−rl1)⋅x^1]最后在乘以 x ^ 1 \hat{x}_{1} x^1(即 ( [ ( r l 3 − r l 1 ) ⋅ x ^ 1 ] x ^ 1 ([(r_{l3}-r_{l1})\cdot\hat{x}_{1}]\hat{x}_{1} ([(rl3−rl1)⋅x^1]x^1)得到向量(因为此时 x ^ 1 \hat{x}_{1} x^1表示的是x轴的单位向量)。这里操作的目的是能够得到 r l 3 r_{l3} rl3在 x x x轴的分量(这里的 x x x轴是由 r l 1 r_{l1} rl1和 r l 2 r_{l2} rl2组成的)。
2. ( r l 3 − r l 1 ) − [ ( r l 3 − r l 1 ) ⋅ x ^ 1 ] x ^ 1 (r_{l3}-r_{l1})-[(r_{l3}-r_{l1})\cdot\hat{x}_{1}]\hat{x}_{1} (rl3−rl1)−[(rl3−rl1)⋅x^1]x^1最后相减得到了垂直于 x x x轴的向量 y 1 y_{1} y1(而且这个向量 y 1 y_{1} y1是过 r l 3 r_{l3} rl3的)。
如图:
单位向量:
y ^ 1 = y 1 ∣ ∣ y 1 ∣ ∣ \hat{y}_{1}=\frac{y_{1}}{||y_{1}||} y^1=∣∣y1∣∣y1
是左坐标系中新y轴的方向向量。最后,我们使用叉乘::
z ^ 1 = x 1 ^ × y ^ 1 \hat{z}_{1}=\hat{x_{1}}\times\hat{y}_{1} z^1=x1^×y^1
得到左坐标系中新 z z z轴的方向向量。同样的,我们能在右坐标系中得到相应的 x ^ r , y ^ r , z ^ r \hat{x}_{r},\hat{y}_{r},\hat{z}_{r} x^r,y^r,z^r。我们所求的旋转就是将 x ^ 1 , y ^ 1 , z ^ 1 \hat{x}_{1},\hat{y}_{1},\hat{z}_{1} x^1,y^1,z^1分别变换到 x ^ r , y ^ r , z ^ r \hat{x}_{r},\hat{y}_{r},\hat{z}_{r} x^r,y^r,z^r的旋转。现在将列向量邻接起来形成矩阵 M 1 M_{1} M1和 M r M_{r} Mr:
M 1 = [ x ^ 1 y ^ 1 z ^ 1 ] M_{1} =\begin{matrix} [\hat{x}_{1}& \hat{y}_{1} &\hat{z}_{1} ] \end{matrix} M1=[x^1y^1z^1] , M r = [ x ^ r y ^ r z ^ r ] M_{r} =\begin{matrix} [\hat{x}_{r}& \hat{y}_{r} &\hat{z}_{r} ] \end{matrix} Mr=[x^ry^rz^r]
给一个左坐标系中的向量 r 1 r_{1} r1,则
M 1 T r 1 M_{1}^{T}r_{1} M1Tr1
给出了矢量r沿着新构造的三角轴(其实就是新坐标系)的分量。将其乘以 M r M_{r} Mr就可以将它映射到右坐标系中,所以:
r r = M r M r T r r r_{r}=M_{r}M^{T}_{r}r_{r} rr=MrMrTrr
如何理解两个上面等式怎么来的?我是这么理解的:这里应该是少说了一个世界坐标系,一共是有三个坐标系,左右手坐标系+一个世界坐标系。上面的等式是都转化成了在世界坐标系下来做等号的。例如:在世界坐标系下有一个点 p p p, p p p乘以 M 1 M_{1} M1得到左手坐标系上的表示为 r 1 r_{1} r1, p p p乘以 M r M_{r} Mr得到右手坐标系上的表示为 r r r_{r} rr,即 r 1 = M 1 p r_{1}=M_{1}p r1=M1p和 r r = M r p r_{r}=M_{r}p rr=Mrp。
所以进一步的,能推出: p = M 1 − 1 r 1 = M 1 T r 1 p=M_{1}^{-1}r_{1}=M_{1}^{T}r_{1} p=M1−1r1=M1Tr1和 r r = M r p = M r M r T r r r_{r}=M_{r}p=M_{r}M^{T}_{r}r_{r} rr=Mrp=MrMrTrr。
从中能够得到旋转矩阵:
R = M r M l T R=M_{r}M_{l}^{T} R=MrMlT
R是一个正交矩阵,因为
M
r
M_{r}
Mr和
M
l
M_{l}
Ml都是正交的。以上就是通过三个点来求旋转的封闭解的方案。注意到它选择性的使用了三个点的信息。事实上,如果我们重编号这些点,我们会得到一个不同的旋转,除非数据是完美的。也要注意,这种方法不能扩展到超过三个点的情况。
即使仅有三个点,我们也应该使用最小二乘法去解这个问题,因为这里的约束大于未知参数的个数(也就是列出来的方程是一个超定方程组,需求其最小二乘解)。平移和比例因子的最小二乘解会在2.C和2.E小节中讲到。寻找最优旋转矩阵在第四章讲到。
转载,侵权请联系!





















 1787
1787











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








