数值优化学习笔记（二）C++实现牛顿法

本篇里面是结合有Armijio condition的实现，所以对步长的选取可能更好一些。
关于最速下降法的实现，在本人的另一篇博客里面也有实现，同时里面也简单介绍了本篇文章里面要实现的函数RosenBrock。
牛顿法是对函数进行二阶泰勒展开，会使用到函数的二阶高维信息，所以更精确一些，但随之而来的就是计算二维Hessian时带来的计算量，求逆矩阵时甚至达到了$O(n_3)$。
以下是函数的梯度计算结果和Hessian计算结果：

具体的牛顿法实现步骤在之前的博客里面也有介绍，这里我把流程截图了过来（请原谅没有太多时间把这些敲成latex公式）

下图是输入为（1.5，3）时的输出：

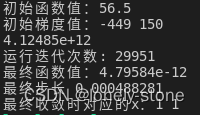
具体代码实现：

#include<iostream>
#include<algorithm>
#include<fstream>
#include<iomanip>
#include<chrono>
#include<ctime>
#include<sstream>
#include<vector>
#include<cmath>
#include<iterator>
#include<map>
#include<string.h>

#include <complex>
#include <set>
#include <Eigen/StdVector>
#include <Eigen/Dense>
#include <Eigen/Core>
#include <unsupported/Eigen/MatrixFunctions>

using namespace std;
using namespace Eigen;

// 函数值
double RosenBrock(const Eigen::VectorXd x)
{
    double res = 0.0;
    for(int i = 0; i <= int(x.size()/2 - 1); ++i)
    {
        res += 100 * pow(pow(x(2*i),2) - x(2*i+1), 2) + pow(x(2*i) - 1, 2);
    }
    return res;
} 
// 算函数梯度
Eigen::VectorXd gradient(const Eigen::VectorXd x)
{
    Eigen::VectorXd res(x.size());
    for(int i = 0; i <= int(x.size()/2 - 1); ++i)
    {
        res(2*i) = 400 * (pow(x(2*i), 3) - x(2*i)*x(2*i+1)) + 2 * (x(2*i) - 1);
        res(2*i+1) = -200 * (pow(x(2*i), 2) - x(2*i+1));
    }
    return res;
}
// Hessian
Eigen::MatrixXd Hessian(const Eigen::VectorXd x)
{
    Eigen::MatrixXd H(x.size(), x.size());
    for(int i = 0; i < x.size()/2; ++i){
        H(2*i,2*i) = 400 * (3 * pow(x(2*i), 2) - x(2*i+1)) + 2;
        H(2*i,2*i+1) = -400 * x(2*i);
        H(2*i+1,2*i) = -400 * x(2*i);
        H(2*i+1,2*i+1) = 200;
    }
    return H;
}

int main() {
    Eigen::VectorXd x(2);
    x << 1.5,3;
    cout <<"初始函数值：" << RosenBrock(x) <<endl;
    
    // iteration initialization
    double t = 1.0;
    double c = 0.5;
    double sigma = 1e-5;
    Eigen::VectorXd gra = gradient(x);
    Eigen::VectorXd d = gra * (-1);
    cout <<"初始梯度值：";
    for(int i = 0; i < x.size(); ++i) cout << gra(i) << " ";
    cout << endl;

    cout << RosenBrock(x + d) <<endl;
    int cnt = 0;

    while(sqrt(gra.adjoint()*gra) > sigma)
    {
        Eigen::VectorXd tt = gra * c *t;
        double tmp = d.adjoint() * tt;
        while(RosenBrock(x + d*t) > RosenBrock(x) + tmp)
        {
            // update
            t /= 2;
            tt = gra * c *t;
            tmp = d.adjoint() * tt;
        }
        x += d*t;
        Eigen::MatrixXd M = Hessian(x);
        gra = gradient(x);
        d = M.inverse() * gra * (-1);
        ++ cnt;
    }
    cout <<"运行迭代次数: "<<  cnt <<endl;
    cout << "最终函数值：" << RosenBrock(x) <<endl;
    cout << "最终步长 " << t <<endl;
    cout << "最终收敛时对应的x：";
    for(int i = 0; i < x.size(); ++i) cout << x(i) << " ";
    cout << endl;
    return 1;
}