谱方法学习笔记-下(超详细)

谱方法学习笔记📒

谱方法学习笔记-上(超详细)
声明：鉴于CSDN使用 $KaTeX$ 渲染公式，$\text{KATEX}$ 与 $LaTeX$ 不同，不支持直接的交叉引用命令，如\label和\eqref。$\text{KATEX}$专注于数学公式的呈现，而不提供完整的文档生成功能。因此，为了保证显示正常，本文中所有公式均已删除编号和交叉引用。由此可能导致一些可读性上的不便，请读者谅解。

傅里叶谱方法求解基本偏微分方程—二维 Schnakenberg 模型

Schnakenberg模型是一种描述化学反应动力学的数学模型，旨在研究化学反应中自组织现象和空间模式的形成。

该模型最早由德国化学家Heinrich Otto Wieland提出，后由德国数学家Theodor Schnakenberg在其博士论文中进行了推导和解析，并得到了该模型的名字。

Schnakenberg模型的意义在于，它可以模拟一系列反应中出现的自组织现象，例如化学波、化学斑图、化学分叉等。这些现象是由于反应物浓度分布在空间上的不均匀性导致的，通过Schnakenberg模型可以更好地理解这些现象，并为实验提供一定的指导和验证。

此外，Schnakenberg模型还可以应用于其他领域，例如生物学、物理学、生态学等。在这些领域中，该模型可以用于研究许多自组织现象，例如细胞分裂、病毒传播、生态系统演化等。

这个模型描述的是两种化学物质之间的反应过程。具体来说，化学物质 $u$ 会被消耗掉，同时生成化学物质$v$。反应速率的大小取决于$u$ 和$v$的浓度，而扩散系数则描述了物质在空间中的扩散速度。

Schnakenberg模型有许多有趣的特性和行为。例如，在某些参数范围内，这个模型的解可以显示出空间上的分布和时间上的演化，形成有序的斑图（patterns）。这些斑图包括静态和动态的形态，它们的形状和数量取决于模型参数的取值。这种有序结构的出现和演化，可以通过Schnakenberg模型来解释和理解实验室中观察到的许多化学反应和生物学现象。具体来说，当模型的参数取值适当时，Schnakenberg模型的解会形成一个包含不同浓度级别的周期性结构。这种周期性结构被称为Turing结构，是由Alan Turing在1952年提出的一种理论模型。Turing结构是许多自组织系统中的一种普遍现象，例如斑马条纹、蝴蝶翅膀上的斑点等。
在Schnakenberg模型中，Turing结构的出现是由反应和扩散之间的相互作用所导致的。具体来说，当扩散系数足够大时，化学物质可以在空间上扩散，使得浓度分布均匀。但当反应速率较慢时，这些化学物质在局部区域内聚集起来，并且在一定的空间尺度上发生反应。这个过程会导致局部区域内的浓度发生变化，从而形成周期性的结构。
需要注意的是，Turing结构的出现是非线性动力学的一个重要特征。这种结构的产生和演化需要考虑多个因素之间的相互作用，因此通常需要使用数值计算和数学分析的方法来研究其性质和行为。

需要注意的是，Schnakenberg模型是一种简化的模型，它假设了化学物质的浓度在空间和时间上均匀分布，没有考虑一些具体的生物或化学体系的细节和复杂性。因此，这个模型只能作为一种基本的参考模型，而不是具体体系的精确描述。

近年来，Schnakenberg模型被广泛应用于不同领域的研究中，包括流体力学、生物学、材料科学等。这个模型的理论和数值分析方法也在不断地发展和完善，为我们深入理解和探究复杂动态系统的性质和行为提供了有力的工具和平台。

斑图（pattern）是一类普遍存在于自然界、在时间或空间上具有某种规律的非均匀宏观结构。反应-扩散系统 (reaction-diffusion system) 是斑图理论中研究得最为广 泛的系统, 它起源于化学反应系统, 但又不局限于此, 还广泛应用于生物学、物理学、医学、金融学等。Schnakenberg 模型是反应-扩散系统中的一个有趣的模型, 数学形式如下:
$$\{\begin{array}{l}\frac{\partial u}{\partial t}=\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}\right)u+\gamma \left(a-u+u^{2}v\right)\\ \frac{\partial v}{\partial t}=d\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}\right)v+\gamma \left(b-u^{2}v\right)\end{array}$$
其中, $u$ 和 $v$ 可看做两种化学反应物质的浓度, $x、y$ 为空间坐标, $t$ 为时间, $a、b、d$ 、 $\gamma$ 为常数。对式 (3-38) 做二维傅里叶变换, 可将其转化为偏微分方程组:

$$\{\begin{array}{l}\frac{\partial \hat{u}}{\partial t}=-\left(k_x^2+k_y^2\right)\hat{\hat{u}}+\gamma \cdot F\left\{a-F^{-1}[\hat{u}]+F^{-1}[\hat{u}{]}^2{F}^{-1}[\hat{v}]\right\}\\ \frac{\partial \hat{v}}{\partial t}=-d\left(k_x^2+k_y^2\right)\hat{v}+\gamma \cdot F\left\{b-F^{-1}[\hat{u}{]}^2{F}^{-1}[\hat{v}]\right\}\end{array}$$

参数取值为: $a=0.1,b=0.8,d=26,\gamma =100$ 。为了得到靶型波, 将初始条件设置为: $u$ 在 $x-y$ 平面原点处为 1 , 在其他位置为 $0,v$ 在整个 $x-y$ 平面上均为 1 。利用傅里叶谱方法 求解该模型的代码如下。

主程序代码

clear all; close all;
L=16; N=64;
kx=2*pi/L*[0:N/2-1 -N/2:-1]; ky=kx;
[kX,kY]=meshgrid(kx,ky);
K2=kX.^2+kY.^2;
%初始条件
u=zeros(N); u(N/2,N/2)=1; v=ones(N);
ut=fft2(u); vt=fft2(v);
uvt=[ut(:); vt(:)];
%求解
a=0.1; b=0.8; d=26; gamma=100; t=[0:0.1:0.3];
[t,uvtsol]=ode45('schnakenberg',t,uvt,[],K2,N,gamma,a,b,d);
%画图
for n=1:4
    subplot(2,2,n)
    gca=pcolor(ifft2(reshape(uvtsol(n,1:N^2),N,N))); axis off
    set(gca,'LineStyle','none'), shading interp
    title(['t=' num2str(t(n))]), axis('square'),
%     colormap('gray')
end

程序输出的结果如图所示，这与化学实验中观察到的靶型波一致。

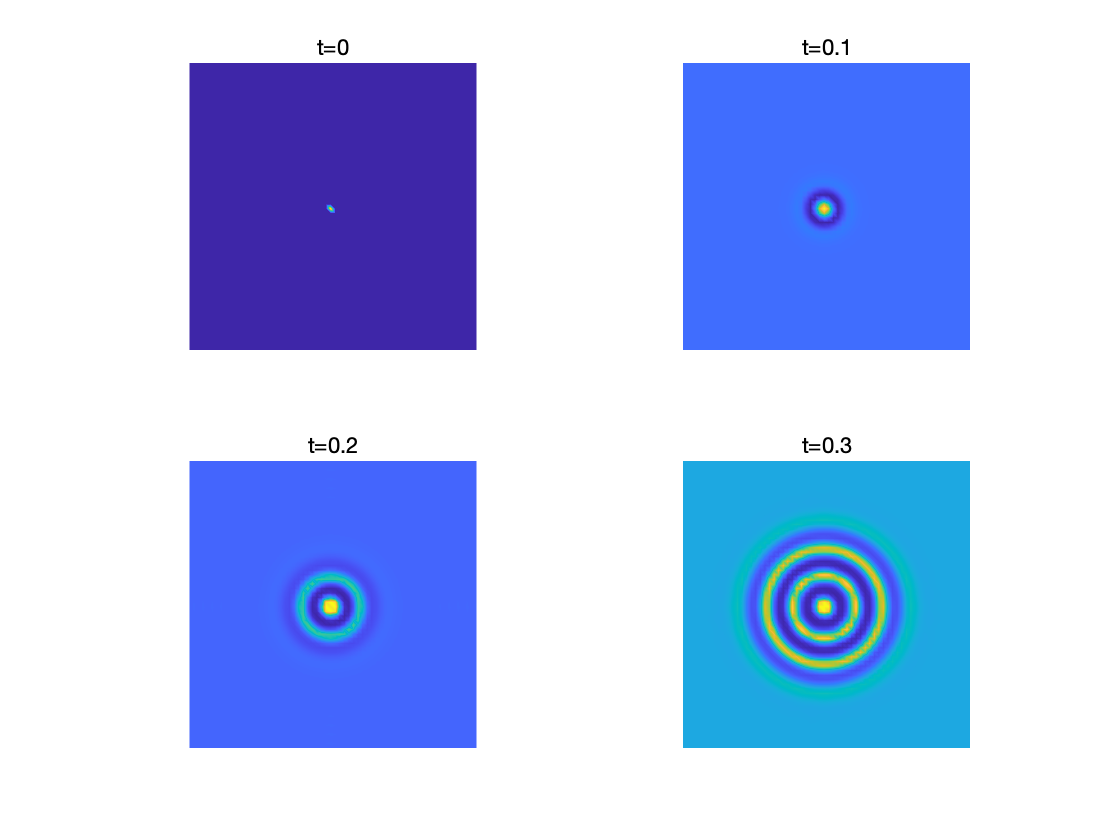
Matlab 将计算结果制作成 gif 动画

引言

求解包含时间的偏微分方程 (组) 将得到随着时间变化的数值结果, 把这样的数据制作成 gif 动画并结合到幻灯片中, 在毕业答辩、小组讨论、课堂教学等场合有着广泛的应用。生动的彩色 gif 动画具有很强的表现力, 令人刮目相看, 大大提高了报告人所讲述理论结果的直观性、生动性、观赏性。

函数介绍

生成 gif 动画主要用到 $4$ 个函数: getframe、frame2im、rgb2ind、imwrite。

1. getframe 函数的一般调用形式为: F=getframe(h), 其作用是截取句柄为 h 的窗口内的一帧图像。

2. frame2im 函数的作用是把一帧截图转为图像数据。

3. rgb2ind 函数的作用是将 RGB 图像转换为索引图像, 一般调用形式为: [X, map]= rgb2ind(RGB,n) 。其中, X、map 分别为转换后的图像数据和颜色表数据, RGB 为转换前的图像数据, n 指定 map 中的颜色数。

4. imwrite 函数的作用是将图像数据写入图像文件, 一般调用形式为: imwrite(X,map,filename,fmt,Param1,Val1,Param2,Val2...)。其中, X、map 意义同上, filename 为文件名, fmt 为文件格式,Param1,Val1,Param2,Val2... 为若干可选参数及其取值。如：参数 LoopCount 为动画的循环播放次数, 这里设为 inf, 即无穷大。参数 DelayTime 为每帧间隔时间, 单位秒。参数 WriteMode 为写入文件的模式, 有覆盖 overwrite (默认) 和追加 append 两种选择。

Matlab源代码

生成 gif 动画的示例代码如下:

---

clear
clc
close
x=-1:0.02:1;y=x;
[X,Y]=meshgrid(x,y);
filename='test.gif';
for a=1:10
    u=a*exp(-10*(X.^2+Y.^2));
    mesh(x,y,u),axis([-1 1 -1 1 0 10]),drawnow
    im=frame2im(getframe(gcf));
    [A,map]=rgb2ind(im,256);
    if a==1
        %先以覆盖模式写入指定的gif文件
        imwrite(A,map,filename,'gif','LoopCount',Inf,'DelayTime',0.1);
    else
        %再以追加模式将每一帧写入gif文件
        imwrite(A,map,filename,'gif','WriteMode','append','DelayTime',0.1);
    end
end

---

运行代码之后在当前目录下生成 gif 文件, 该动画显示了一个三维高斯函数的峰值逐渐增大的过程。

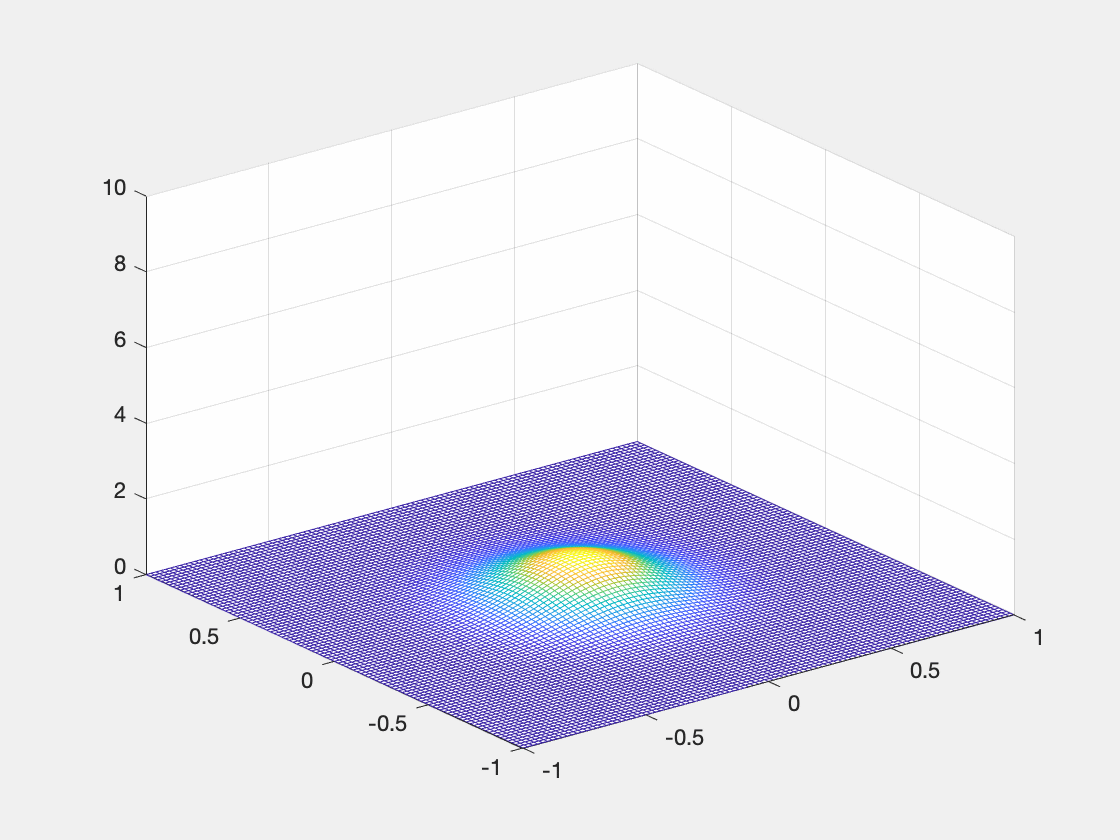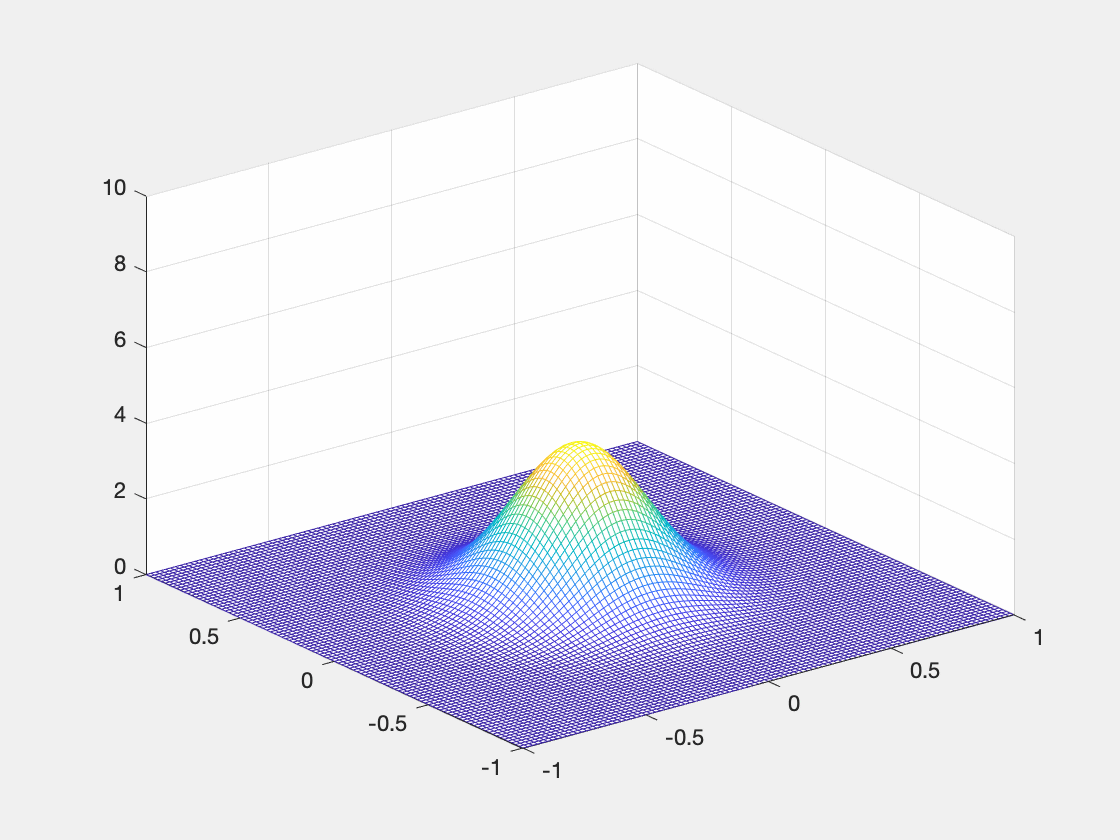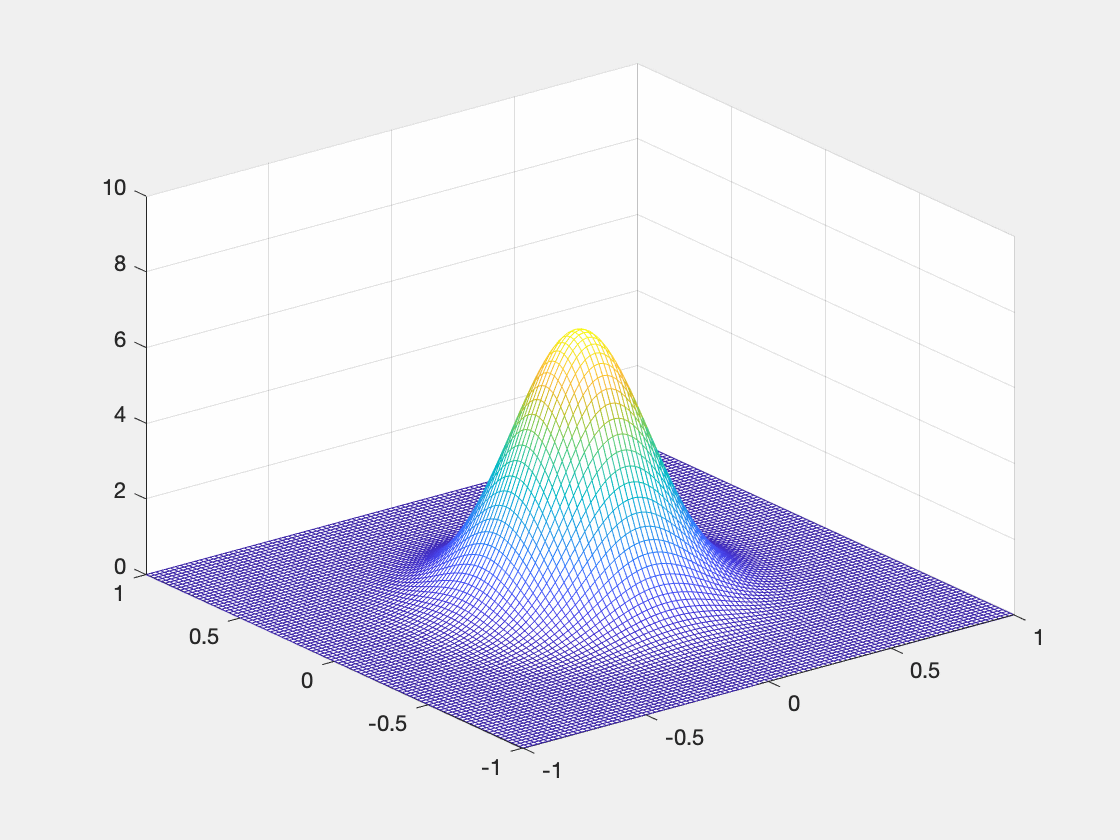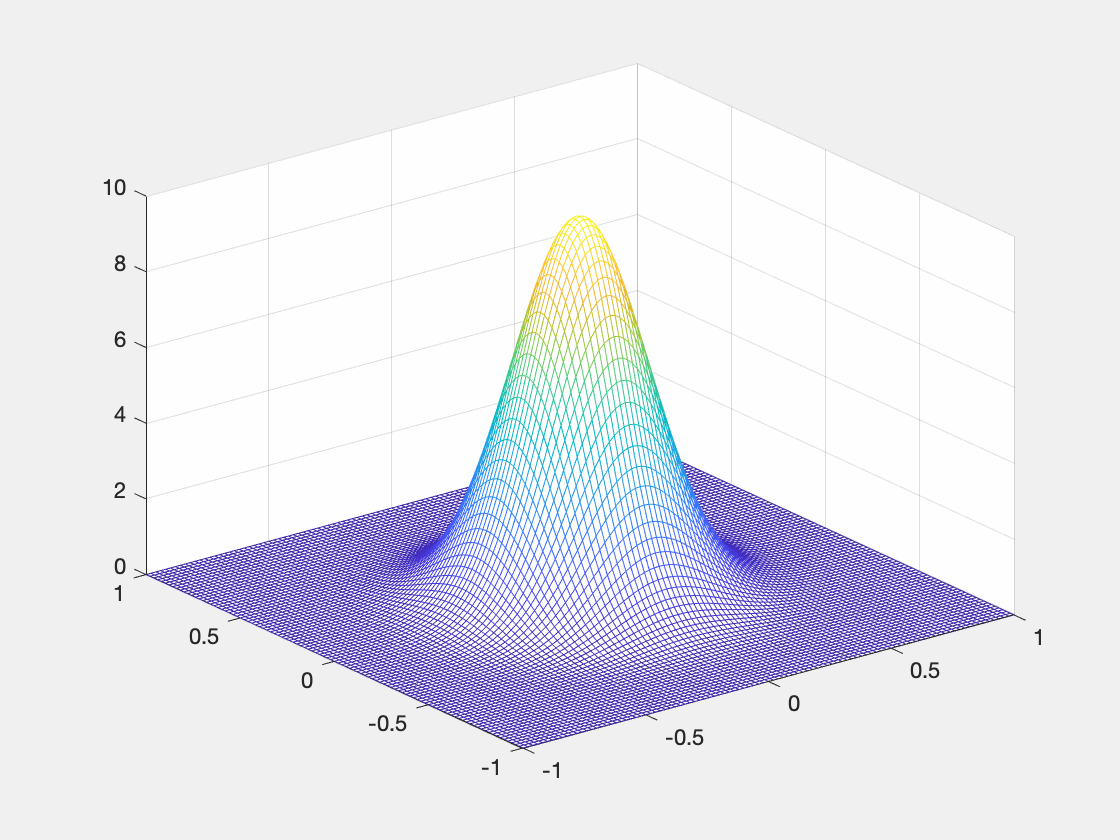
为了更加直观的感受求解 Schnakenberg 模型得到的靶型波，此处结合上述操作将计算结果制作成如下 gif 动画。

修改后的程序源代码：

clear all; close all;
L=16; N=64;
kx=2*pi/L*[0:N/2-1 -N/2:-1]; ky=kx;
[kX,kY]=meshgrid(kx,ky);
K2=kX.^2+kY.^2;
%初始条件
u=zeros(N); u(N/2,N/2)=1; v=ones(N);
ut=fft2(u); vt=fft2(v);
uvt=[ut(:); vt(:)];
%求解
a=0.1; b=0.8; d=26; gamma=100; t=[0:0.01:1];
[t,uvtsol]=ode45('schnakenberg',t,uvt,[],K2,N,gamma,a,b,d);
%画图
filename = 'output.gif'; % 设置保存的gif文件名
for n = 1:length(t)
    gca=pcolor(ifft2(reshape(uvtsol(n,1:N^2),N,N))); axis off
    set(gca,'LineStyle','none'), shading interp
    title(['t=' num2str(t(n))]), axis('square'),
    % colormap('gray')



    % 捕捉当前子图并转换为gif图像帧
    frame = getframe(gcf);
    im=frame2im(getframe(gcf));
    [A,map]=rgb2ind(im,256);

    % 写入gif图像文件
    if n == 1
        %先以覆盖模式写入指定的gif文件
        imwrite(A,map,filename,'gif','LoopCount',Inf,'DelayTime',0.01);
    else
        %再以追加模式将每一帧写入gif文件
        imwrite(A,map,filename,'gif','WriteMode','append','DelayTime',0.01);
    end
end

谱求导矩阵

谱求导矩阵的导出和应用

在生产实践过程中, 某些函数关系的具体表达式是未知的, 只能通过实验测量得到该函数上的一些离散的数据点.所以, 人们希望通过这些离散的数据点构造一个已知函数来近似地描述并替代未知函数.此外, 尽管有些函数的表达式是已知的, 但由于太过复杂繁琐, 不便对其进行理论计算和数值分析, 所以也有必要构造一个简单函数来替代它.

上述问题用数学语言表达为: 已知在区间 $[a,b]$ 上的 $N$ 个位置 $x_1,x_2,\dots ,x_N$ 的函数值 $u_1$, $u_2,\dots ,u_N$, 求一个函数 $p(x)$ 通过所有已知点 $\left(x_1,u_1\right),\left(x_2,u_2\right),\dots ,\left(x_N,u_N\right)$, 即:

$$u_j=p\left(x_j\right),j=1,2,\dots ,N$$

其中, 用 $p(x)$ 近似未知函数的方法称为插值法 (interpolation), $p(x)$ 称为插值函数.下面介绍用谱方法确定插值函数 $p(x)$ 的过程, 并将其用于计算离散数据的各阶导数、偏微分方程 (组) 的数值求解.

谱方法插值

考虑在区间 $[0,2\pi ]$ 上、具有周期性边界条件的插值问题.在此区间上间距为 $h$ 的 $N$ 个位置 $x_1,x_2,\dots ,x_N$ 对应的函数值为 $u_1,u_2,\dots ,u_N$ .其中, $x_j=jh,h=2\pi /N$, 即:

$$\frac{\pi }{h}=\frac{N}{2}$$

在推导前先做 3 点说明:

(1) 选择区间 $[0,2\pi ]$ 是为了方便讨论, 在该区间上得出的结论同样适用于对其平移得到的其他区间 (如 $[-\pi ,\pi ]$ ), 并可以通过乘以缩放因子方便地将结论转化到其他长度非 $2\pi$的任意区间上 (如 $[-L,L])$ .

(2) 所谓周期性边界条件, 是指 $N$ 个函数值 $u_1,u_2,\dots ,u_N$ 可等效地看做是无穷多个函数值 $\dots ,u_{-1},u_0,u_1,\dots ,u_{N-1},u_N,u_{N+1},\dots$ 的一部分, 并存在 $u_{j+mN}=u_j$ 的关系 ( $m$ 为任意整数).这里把讨论的函数当做周期为 $2\pi$ 的周期函数处理.

(3) $N$ 的奇偶会导致接下来的推导细节有所差异, 但过程是相似的, 所以此处只分析 $N$ 为偶数的情况.

若对序列 $u_1,u_2,\dots ,u_N$ 做离散傅里叶变换, 那么空域（时域）上的间隔 $h$ 决定了频域上的区间为 $[-\pi /h,\pi /h]$ .由式 % \eqref{4-2} , 该区间也可写为 $[-N/2,N/2]$ .本部分中的离散傅里叶变换对定义为:

$$\begin{array}{r}{\hat{u}}_k=h\sum _{j=1}^N{\mathrm{e}}^{-\mathrm{i}k{x}_j}{u}_j,k=-\frac{N}{2}+1,\dots ,\frac{N}{2}{u}_j=\frac{1}{2\pi }\sum _{k=-N/2+1}^{N/2}{\mathrm{e}}^{\mathrm{i}k{x}_j}{\hat{u}}_k,j=1,\dots ,N\end{array}$$

这与前面给出的 Matlab 中离散傅里叶变换对的定义略有不同, 但实质是一样的.注意到式 % \eqref{4-4} 中的频率分量并不是完全对称的, $k$ 中有 $0、\pm 1、\pm 2、\cdots \cdots 、\pm (N/2-1)、N/2$,却没有 $-N/2$, 这在求解插值函数时会引起一些小小的问题.所以, 令 ${\hat{u}}_{-N/2}={\hat{u}}_{N/2}$, 并重新定义离散傅里叶逆变换为:

$$u_j=\frac{1}{2\pi }\sum _{k=-N/2}^{N/2}{}^{\prime }{\mathrm{e}}^{\mathrm{i}k{x}_j}{\hat{u}}_k,j=1,\dots ,N$$

其中, “ ${\Sigma }^{\prime }$ 代表求和时在 $k=\pm N/2$ 的项上乘以 $1/2$ .需要强调的是, 式 % \eqref{4-3} 和式 % \eqref{4-4} 仍然是离散傅里叶变换对的定义, 式 % \eqref{4-5} 仅是用于确定插值函数 $p(x)$ 的.求 $p(x)$ 时需要把式 % \eqref{4-5} 中的 $x_j=jh$ 推广到 $[0,2\pi ]$ 上的任意实数 $x$, 即:

$$p(x)=\frac{1}{2\pi }\sum _{k=-N/2}^{N/2}{}^{\prime }{\mathrm{e}}^{\mathrm{i}kx}{\hat{u}}_k,x\in [0,2\pi ]$$

确定插值函数的步骤是这样的：先用式 % \eqref{4-3} 将序列 $u_1,u_2,\dots ,u_N$ 变换为 ${\hat{u}}_{-N/2+1}$, ${\hat{u}}_{-N/2+2},\dots ,{\hat{u}}_{N/2}$, 令 ${\hat{u}}_{-N/2}={\hat{u}}_{N/2}$, 再根据序列 ${\hat{u}}_{-N/2},{\hat{u}}_{-N/2+1},\dots ,{\hat{u}}_{N/2}$ 通过式 % \eqref{4-6} 得到 $p(x)$ .这样得到的插值函数 $p(x)$ 可用来求序列 $u_1,u_2,\dots ,u_N$ 在 $x_j$ 处的各阶导数, 即:

$${\frac{{\partial }^{n}p(x)}{\partial x^n}|}_{x=x_j}$$

上面介绍的是通过谱方法计算插值函数 $p(x)$ 来估算序列 $u_1,u_2,\dots ,u_N$ 在 $x_j$ 处的导数的基本原理.接下来, 为了把上述过程转化为方便的矩阵运算, 采用如下思路: 首先求出周期 $\delta$ 函数的插值函数 $S_N(x)$, 然后将任意序列 $u_1,u_2,\dots ,u_N$ 写为周期 $\delta$ 函数的线性组合, 进而可把它的插值函数 $p(x)$ 写为 $S_N(x)$ 的线性组合, 最后找到 $p(x)$ 和 $S_N(x)$ 在 $x_1,x_2,\dots ,x_N$ 处导数的关系并写为矩阵形式, 给出针对任意序列 $u_1,u_2,\dots ,u_N$ 的谱求导矩阵.

谱求导矩阵

周期 $\delta$ 函数定义为:

$${\delta }_j=\{\begin{array}{ll}1,& (j\%N=0)\\ 0,& (j\%N\ne 0)\end{array}$$

其中, 百分号 “ $\%$ ” 代表求余运算, 周期 $\delta$ 函数在 $j=mN$ ( $m$ 为任意整数) 时取值为 1 ,其他情况为 0 , 它所对应的横坐标为 $x_j=jh$ .利用式 % \eqref{4-3} 求周期 $\delta$ 函数的离散傅里叶变换, 结果为一常数 $h$ :

$${\hat{\delta }}_k=h\sum _{j=1}^N{\mathrm{e}}^{-\mathrm{i}k{x}_j}{\delta }_j=h,k=-\frac{N}{2}+1,\dots ,\frac{N}{2}$$

再利用式 % \eqref{4-6} 求周期 $\delta$ 函数的插值函数:

$$\begin{array}{rl}p(x)& =\frac{h}{2\pi }\sum _{k=-N/2}^{N/2}{}^{\prime }{\mathrm{e}}^{\mathrm{i}kx}\\ & =\frac{h}{2\pi }\left(\frac{1}{2}\sum _{k=-N/2}^{N/2-1}{\mathrm{e}}^{\mathrm{i}kx}+\frac{1}{2}\sum _{k=-N/2+1}^{N/2}{\mathrm{e}}^{\mathrm{i}kx}\right)\\ & =\frac{h}{2\pi }\left(\frac{1}{2}{\mathrm{e}}^{-\frac{\mathrm{i}}{2}x}\sum _{k=-N/2+1/2}^{N/2-1/2}{\mathrm{e}}^{\mathrm{i}kx}+\frac{1}{2}{\mathrm{e}}^{\frac{\mathrm{i}}{2}x}\sum _{k=-N/2+1/2}^{N/2-1/2}{\mathrm{e}}^{\mathrm{i}kx}\right)\\ & =\frac{h}{2\pi }\cos (x/2)\sum _{k=-N/2+1/2}^{N/2-1/2}{\mathrm{e}}^{\mathrm{i}kx}\\ & =\frac{h}{2\pi }\cos (x/2)\frac{{\mathrm{e}}^{\mathrm{i}(-N/2+1/2)x}-{\mathrm{e}}^{\mathrm{i}(N/2+1/2)x}}{1-{\mathrm{e}}^{\mathrm{i}x}}\\ & =\frac{h}{2\pi }\cos (x/2)\frac{{\mathrm{e}}^{-\mathrm{i}(N/2)x}-{\mathrm{e}}^{\mathrm{i}(N/2)x}}{{\mathrm{e}}^{-\mathrm{i}x/2}-{\mathrm{e}}^{\mathrm{i}x/2}}\\ & =\frac{h}{2\pi }\cos (x/2)\frac{\sin (Nx/2)}{\sin (x/2)}\end{array}$$

由式 % \eqref{4-2} , 最终得到的周期 $\delta$ 函数的插值函数为周期 sinc 函数 $S_N$ :

$$S_N(x)=\frac{\sin (\pi x/h)}{(2\pi /h)\tan (x/2)}$$

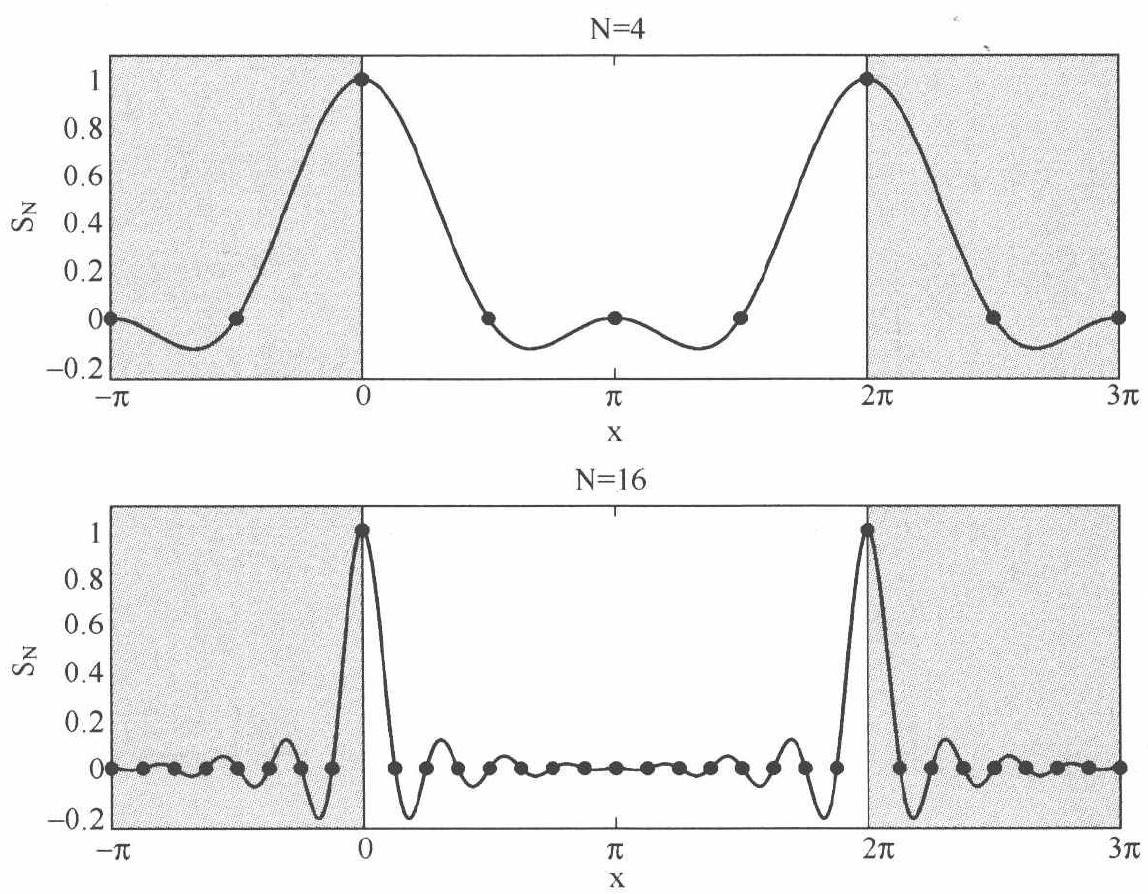
可以证明, ${S_N(x)|}_{x\to 0}=1$ .下图（曲线为周期 $\mathrm{sinc}$ 函数, 黑点为周期 $\delta$ 函数, 上下两图分别对应 $N=4$ 和 $N=16$） 显示了周期 $\delta$ 函数以及它的插值函数一一周期 sinc 函数 $S_N(x)$, 二者的周期均为 $2\pi$, 无论 $N$ 取值为 4 还是 16 , 后者都精确、巧妙地经过了前者的所有离散点.

若将区间 $[0,2\pi ]$ 上的序列 $u_1,u_2,\dots ,u_N$ 写为周期 $\delta$ 函数的线性叠加, 即:
$$u_j=\sum _{m=1}^N{u}_m{\delta }_{j-m}$$

那么, 将其中的周期 $\delta$ 函数替换为周期 $\mathrm{sinc}$ 函数 $S_N$, 就得到序列 $u_1,u_2,\dots ,u_N$ 的插值函数 $p(x)$ :

$$p(x)=\sum _{m=1}^N{u}_m{S}_N\left(x-x_m\right)$$

注意到 $p(x)$ 就是 $S_N(x)$ 的线性组合,如果用 $p(x)$ 来估算序列 $u_1,u_2,\dots ,u_N$ 在 $x_j=jh$ 处的 1 阶导数, 则有:

$$p^{\prime }\left(x_j\right)=\sum _{m=1}^N{u}_m{S}_N^{\prime }\left(x_j-x_m\right)$$

其中, $x_j-x_m=(j-m)h$ .将上式写为矩阵形式:

$$\left(\begin{array}{c}{p}^{\prime }\left(x_1\right)\\ p^{\prime }\left(x_2\right)\\ p^{\prime }\left(x_3\right)\\ ⋮\\ p^{\prime }\left(x_N\right)\end{array}\right)=\left(\begin{array}{ccccc}{S}_N^{\prime }(0)& S_N^{\prime }(-h)& S_N^{\prime }(-2h)& \cdots & S_N^{\prime }((1-N)h)\\ S_N^{\prime }(h)& S_N^{\prime }(0)& S_N^{\prime }(-h)& & \\ S_N^{\prime }(2h)& S_N^{\prime }(h)& S_N^{\prime }(0)& & \\ ⋮& & & \ddots & \\ S_N^{\prime }((N-1)h)& & & & \end{array}\right)\left(\begin{array}{c}{u}_1\\ u_2\\ u_3\\ ⋮\\ u_N\end{array}\right)$$

因此, 只需在向量 ${\left(u_1,u_2,\dots ,u_N\right)}^{\mathrm{T}}$ 上乘以一个 $N$ 阶方阵即可得到由它的谱方法插值函数 $p(x)$的导数组成的向量 ${\left(p^{\prime }\left(x_1\right),p^{\prime }\left(x_2\right),\dots ,p^{\prime }\left(x_N\right)\right)}^{\mathrm{T}}$, 这个 $N$ 阶方阵就是谱求导矩阵 (spectral differentiation matrix).下文用 ${\mathbf{D}}_N$ 来表示 1 阶 $N\times N$ 谱求导矩阵, ${\mathbf{D}}_N^{(n)}$ 表示 $n$ 阶 $N\times N$ 谱求导矩阵.周期 $\mathrm{sinc}$ 函数 $S_N(x)$ 在 $x_j=jh$ 处的 1 阶导数为:

$$S_N^{\prime }\left(x_j\right)=\{\begin{array}{cc}0,& (j\%N=0)\\ (-1{)}^j/2\cdot \cot (jh/2),& (j\%N\ne 0)\end{array}$$

将其代入到式 % \eqref{4-15} 中的 $N$ 阶方阵, 得到 1 阶谱求导矩阵:

$${\mathbf{D}}_N=\left(\begin{array}{ccccc}0& & & & -\frac{\cot (1h/2)}{2}\\ -\frac{\cot (1h/2)}{2}& \ddots & & \ddots & \frac{\cot (2h/2)}{2}\\ \frac{\cot (2h/2)}{2}& \ddots & & -\frac{\cot (3h/2)}{2}& \\ -\frac{\cot (3h/2)}{2}& & \ddots & & ⋮\\ ⋮& \ddots & \ddots & \frac{\cot (1h/2)}{2}& \\ \frac{\cot (1h/2)}{2}& & & & 0\end{array}\right)$$

类似地, 还可以得到高阶谱求导矩阵.周期 $\mathrm{sinc}$ 函数 $S_N(x)$ 在 $x_j=jh$ 处的 2 阶导数为:

$$S_N^{\prime \prime }\left(x_j\right)=\{\begin{array}{cc}-\frac{{\pi }^2}{3h^2}-\frac{1}{6},& (j\%N=0)\\ -\frac{(-1{)}^j{\csc }^2(jh/2)}{2},& (j\%N\ne 0)\end{array}$$

那么, 2 阶谱求导矩阵为:

$$D_N^{(2)}=\left(\begin{array}{ccc}\ddots & ⋮& \\ \ddots & -\frac{1}{2}{\csc }^2\left(\frac{2h}{2}\right)& \\ \ddots & \frac{1}{2}{\csc }^2\left(\frac{1h}{2}\right)& \\ & -\frac{{\pi }^2}{3h^2}-\frac{1}{6}& \\ & \frac{1}{2}{\csc }^2\left(\frac{1h}{2}\right)& \ddots \\ & -\frac{1}{2}{\csc }^2\left(\frac{2h}{2}\right)& \ddots \\ & ⋮& \ddots \end{array}\right)$$

周期 sinc 函数 $S_N(x)$ 在 $x_j=jh$ 处的 3 阶导数为:

$$S_N^m\left(x_j\right)=\{\begin{array}{cc}0,& (j\%N=0)\\ (-1{)}^j\cot \left(\frac{jh}{2}\right)\left[\frac{3}{4}{\csc }^2\left(\frac{jh}{2}\right)-\frac{{\pi }^2}{2h^2}\right],& (j\%N\ne 0)\end{array}$$

同样得到 3 阶谱求导矩阵:
$$D_N^{(3)}=(\begin{array}{cccc}0& & & -\cot \left(\frac{1h}{2}\right)\left[\frac{3}{4}{\cos }^2\left(\frac{1h}{2}\right)-\frac{{\pi }^2}{2h^2}\right]\\ -\cot \left(\frac{1h}{2}\right)\left[\frac{3}{4}{\csc }^2\left(\frac{1h}{2}\right)-\frac{{\pi }^2}{2h^2}\right]& \ddots & \ddots & \cot \left(\frac{2h}{2}\right)\left[\frac{3}{4}{\csc }^2\left(\frac{2h}{2}\right)-\frac{{\pi }^2}{2h^2}\right]\\ \cot \left(\frac{2h}{2}\right)\left[\frac{3}{4}{\csc }^2\left(\frac{2h}{2}\right)-\frac{{\pi }^2}{2h^2}\right]& & \ddots & -\cot \left(\frac{3h}{2}\right)\left[\frac{3}{4}{\csc }^2\left(\frac{3h}{2}\right)-\frac{{\pi }^2}{2h^2}\right]\\ -\cot \left(\frac{3h}{2}\right)\left[\frac{3}{4}{\csc }^2\left(\frac{3h}{2}\right)-\frac{{\pi }^2}{2h^2}\right]& \ddots & & ⋮\\ ⋮& \ddots & \ddots & \cot \left(\frac{1h}{2}\right)\left[\frac{3}{4}{\csc }^2\left(\frac{1h}{2}\right)-\frac{{\pi }^2}{2h^2}\right]\\ \cot \left(\frac{1h}{2}\right)\left[\frac{3}{4}{\csc }^2\left(\frac{1h}{2}\right)-\frac{{\pi }^2}{2h^2}\right]& & & 0\end{array})$$

构造 $n$ 阶谱求导矩阵 ${\mathbf{D}}_N^{(n)}$ 的一般方法为:

(1) 求周期 sinc 函数 $S_{N}(x)$ 在 $x_{j}=j h$ 处的 $n$ 阶导数 $S_{N}^{(n)}\left(x_{j}\right)$ .

(2) $\boldsymbol{D}_{N}^{(n)}$ 的第 1 列为 $\left(S_{N}^{(n)}\left(x_{N}\right), S_{N}^{(n)}\left(x_{1}\right), S_{N}^{(n)}\left(x_{2}\right), \ldots, S_{N}^{(n)}\left(x_{N-1}\right)\right)^{\mathrm{T}}$, 第 2 列为 $\left(S_{N}^{(n)}\left(x_{N-1}\right)\right.$, $\left.S_{N}^{(n)}\left(x_{N}\right), S_{N}^{(n)}\left(x_{1}\right), \ldots, S_{N}^{(n)}\left(x_{N-2}\right)\right)^{\mathrm{T}}$, 第 3 列为 $\left(S_{N}^{(n)}\left(x_{N-2}\right), S_{N}^{(n)}\left(x_{N-1}\right), S_{N}^{(n)}\left(x_{N}\right), \ldots, S_{N}^{(n)}\left(x_{N-3}\right)\right)^{\mathrm{T}} \cdots \cdots$依此类推.

此外, 周期函数 $S_N^{(n)}(x)$ 的奇偶性是由 $n$ 的奇偶决定的, 这在构造 ${\mathbf{D}}_N^{(n)}$ 时可以产生一些便利:

$${\frac{{\partial }^n{S}_N(x)}{\partial x^n}|}_{x=x_j}={(-1{)}^n\frac{{\partial }^n{S}_N(x)}{\partial x^n}|}_{x=x_{N-j}}$$

当 $n$ 为奇数时, 必有:

$${\frac{{\partial }^n{S}_N(x)}{\partial x^n}|}_{x=x_j}=0,j\%N=0$$

当 $n$ 为偶数时, $S_N^{(n)}(x)$ 在 $x=x_j$ 处 $(j\%N=0)$ 的取值是无穷小/无穷小的形式, 需要用洛必达法则求它的极限, 即:

$${\frac{{\partial }^n{S}_N(x)}{\partial x^n}|}_{x=x_j}=\underset{x\to 0}{\lim }\frac{{\partial }^n{S}_N(x)}{\partial x^n},j\%N=0$$

人工计算 $S_N(x)$ 的 $n$ 阶导数的工作量随着阶数 $n$ 的增大而显著增加, 比较省时省力的方法是利用 Matlab 的符号运算功能, 调用 diff 函数和 limit 函数求导、求极限, 并结合 toeplitz 函数, 可实现程序自动生成 ${\mathbf{D}}_N^{(n)}$, 有兴趣的读者可以自行尝试.

由于谱求导矩阵 ${\mathbf{D}}_N^{(n)}$ 是在计算区间长度为 $2\pi$ 的前提下构造的, 所以若实际的计算区间长度为 $L$, 则必须在 ${\mathbf{D}}_N^{(n)}$ 上乘以缩放系数才可保证结果正确, 即: $(2\pi /L{)}^n{\mathbf{D}}_N^{(n)}$ .

下面给出使用谱求导矩阵 ${\mathbf{D}}_N、{\mathbf{D}}_N^{(2)}、{\mathbf{D}}_N^{(3)}$ 对 $u(x)={\mathrm{e}}^{\sin (\pi x)}$ 求 $1、2、3$ 阶导数, 并与精确解

$u^{\prime }(x)=\pi \cos (\pi x){\mathrm{e}}^{\sin (\pi x)}$

$u^{\prime \prime}(x)=\pi^{2} \mathrm{e}^{\sin (\pi x)}\left[\cos ^{2}(\pi x)-\sin (\pi x)\right] $

$ u^{\prime \prime \prime}(x)=\pi^{3} \mathrm{e}^{\sin (\pi x)} \cos (\pi x)\left[\cos ^{2}(\pi x)-3 \sin (\pi x)-1\right]$

比较的实例.代码如下:

clear all; close all;
L=2; N=32;
x=L/N*[-N/2:N/2-1]'; 
%构造谱求导矩阵
h=2*pi/N; column=[0 0.5*(-1).^(1:N-1).*cot((1:N-1)*h/2)]';
D=(2*pi/L)*toeplitz(column,column([1 N:-1:2]));
column=[-pi^2/(3*h^2)-1/6 -0.5*(-1).^(1:N-1)./sin(h*(1:N-1)/2).^2];
D2=(2*pi/L)^2*toeplitz(column);
column=[0 (-1).^(1:N-1).*cot((1:N-1)*h/2).*( ...
    -pi^2/(2*h^2)+3/4*csc((1:N-1)*h/2).^2)]';
D3=(2*pi/L)^3*toeplitz(column,column([1 N:-1:2]));
%导数的精确解
u=exp(sin(pi*x));
du_exact(:,1)=pi*cos(pi*x).*u;
du_exact(:,2)=pi^2*(cos(pi*x).^2-sin(pi*x)).*u;
du_exact(:,3)=pi^3*cos(pi*x).*(cos(pi*x).^2-3*sin(pi*x)-1).*u;
%谱方法求导
du_Fourier(:,1)=D*u;
du_Fourier(:,2)=D2*u;
du_Fourier(:,3)=D3*u;
error=max(abs(du_exact-du_Fourier));
%画图
labels={'u''(x)','u''''(x)','u''''''(x)'};
for n=1:4
    subplot(2,2,n)
    if n==1
        plot(x,u,'k','LineWidth',1.5)
        xlabel x, ylabel u(x), title('u(x)=e^{sin(\pix)}')
    else
        plot(x,du_exact(:,n-1),'k',x,du_Fourier(:,n-1),'.r' ...
            ,'MarkerSize',13,'LineWidth',1.5)
        title(['Error_{max}=' num2str(error(n-1))])
        xlabel x, ylabel(labels(n-1))
    end
end

如下图（用谱求导矩阵计算 $u(x)={\mathrm{e}}^{\sin (\pi x)}$ 的 $1、2、3$ 阶导数（点）并与精确解（曲线）比较）所示, 曲线为精确的 $u(x)、u^{\prime }(x)、u^{\prime \prime }(x)$ 和 $u^{\prime \prime \prime }(x)$, 点为利用谱求导矩阵计算得到的 $u^{\prime }\left(x_j\right)、u^{\prime \prime }\left(x_j\right)$ 和 $u^{\prime \prime \prime }\left(x_j\right)$ .在 $N$ 的取值仅为 32 的情况下, 用谱求导矩阵计算 $u(x)={\mathrm{e}}^{\sin (\pi x)}$ 的 $1、2、3$ 阶导数与精确解的最大误差分别在 $10^{-14}、10^{-12}、10^{-10}$数量级.

用谱求导矩阵求解偏微分方程的步骤

与之前一样, 待求解的偏微分方程的普遍形式为:

$$\frac{{\partial }^{n}u}{\partial t^n}=Lu+N(u)$$

其中, $u(x,t)$ 为 $x、t$ 的函数, $L$ 代表线性算符, $N(u)$ 为非线性项.通过函数代换可将等号左边的 $n$ 阶导数 ${\partial }^n/\partial t^n$ 降到 1 阶, 所以下面分析式 % \eqref{4-26} 的求解过程, 这与式 % \eqref{4-25} 降阶后得到的方程组的解法是一样的.

$$\frac{\partial u}{\partial t}=Lu+N(u)$$

用谱求导矩阵数值求解式 % \eqref{4-26} 的步骤如下:

(1) 在 $x$ 轴上的计算区间内, 将 $x$ 离散化为 $N$ 个等间距的位置 $\mathbf{x}={\left(x_1,x_2,\dots ,x_N\right)}^{\mathrm{T}}$, 相应地, 将函数 $u$ 离散化为 $N$ 维向量 $\mathbf{u}={\left(u_1,u_2,\dots ,u_N\right)}^{\mathrm{T}}$ .

(2) 在等号右边,将线性算符 $L$ 和非线性项 $N(u)$ 里所有对函数 $u$ 的求导运算替换为谱求导矩阵与向量 $\mathbf{u}$ 的乘运算, 即: ${\partial }^{n}u/\partial x^n\to {\mathbf{D}}_N^{(n)}\mathbf{u}$, 并将 $L$ 和 $N(u)$ 都写成矩阵形式, 得到形如式 % \eqref{4-27} 的微分方程组.注意, 若计算区间长度不是 $2\pi$, 则必须在 ${\mathbf{D}}_N^{(n)}$ 上乘以缩放系数.

(3) 用时间步进法（欧拉法、龙格-库塔法等）数值计算式 % \eqref{4-27} 等号左边的 $\partial /\partial t$,在周期性边界条件下,得到不同 $t$ 处的向量 $\mathbf{u}$ .

$$\frac{\partial }{\partial t}\left(\begin{array}{c}{u}_1\\ u_2\\ u_3\\ ⋮\\ u_N\end{array}\right)=\left(\begin{array}{ccccc}{L}_{11}& L_{12}& L_{13}& \cdots & L_{1N}\\ L_{21}& L_{22}& L_{23}& \cdots & L_{2N}\\ L_{31}& L_{32}& L_{33}& \cdots & L_{3N}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ L_{N1}& L_{N2}& L_{N3}& \cdots & L_{NN}\end{array}\right)\left(\begin{array}{c}{u}_1\\ u_2\\ u_3\\ ⋮\\ u_N\end{array}\right)+N\left[\left(\begin{array}{c}{u}_1\\ u_2\\ u_3\\ ⋮\\ u_N\end{array}\right)\right]$$

针对步骤 2 , 这里以 $L=a\cdot {\partial }^2/\partial x^2+b\cdot \partial /\partial x+c、N(u)=u^3+u^3\cdot {\partial }^{2}u/\partial x^2+f(x)\cdot \partial u/\partial x$ 为例进行说明, $a、b$ 和 $c$ 分别为常数.对线性算符 $L$, 除了将 ${\partial }^n/\partial x^n$ 替换为 ${\mathbf{D}}_N^{(n)}$ 之外,还必须在线性算符的常数 $c$ 上乘以 $N$ 阶单位矩阵 ${\mathbf{I}}_N$, 得到 $N$ 阶方阵 $\mathbf{L}$, 即: $\mathbf{L}=a{\mathbf{D}}_N^{(2)}+b{\mathbf{D}}_N+c{\mathbf{I}}_N$ .注意: Matlab 对矩阵与常数之间的加法是有特殊定义的, 如果忘记在 $c$ 上乘以 ${\mathbf{I}}_N$ 会导致错误, 因为线性算符矩阵 $\mathbf{L}$ 与向量 $\mathbf{u}$ 相乘 $\mathbf{L}\mathbf{u}=\left(a{\mathbf{D}}_N^{(2)}+b{\mathbf{D}}_N+c{\mathbf{I}}_N\right)\mathbf{u}=a{\mathbf{D}}_N^{(2)}\mathbf{u}+b{\mathbf{D}}_N\mathbf{u}+c\mathbf{u}\ne \left(a{\mathbf{D}}_N^{(2)}+b{\mathbf{D}}_N+c\right)\mathbf{u}$ .对非线性项 $N(u)$, 替换 ${\partial }^n\partial x^n$ 为 ${\mathbf{D}}_N^{(n)}$ 时, ${\mathbf{D}}_N^{(n)}$ 与向量 $\mathbf{u}$ 之间的乘法是矩阵乘法, 在 Matlab 中用 *表示.而 $u^3$ 应理解为向量 $\mathbf{u}$ 中的每个元素的立方, 这在 Matlab 中用 . ^3 表示.类似地, $f(\mathbf{x})\cdot \left({\mathbf{D}}_N\mathbf{u}\right)$ 也应处理为 $f(\mathbf{x})$ 和向量 ${\mathbf{D}}_N\mathbf{u}$ 中的每个对应元素的相乘, 在 Matlab 中用 .*表示.所以此时 $Lu+N(u)$ 在 Matlab 中应写为:

(a*D2+b*D1+c*I)*u+u.^3+u.^3.*(D2*u)+f.*(D1*u)

换句话说, 只有谱求导矩阵 ${\mathbf{D}}_N^{(n)}$ 与向量 $\mathbf{u}$ 之间的乘法是矩阵运算, 其余的运算均是在矩阵或向量的元素之间进行的.但也有一个例外,由于线性算符 $L$ 中的常数 $c$ 在矩阵化时乘了单位矩阵 ${\mathbf{I}}_N$, 所以实际上 $c{\mathbf{I}}_N$ 与向量 $\mathbf{u}$ 之间也是矩阵乘法, 这样才能将其与线性算符 $L$ 中的其他项相加: $\mathbf{L}=a{\mathbf{D}}_N^{(2)}+b{\mathbf{D}}_N+c{\mathbf{I}}_N$ .

若方程式 % \eqref{4-26} 再增加一个维度, 等号右边包含了 $u(x,y,t)$ 的 ${\partial }^n/\partial x^n$ 和 ${\partial }^n/\partial y^n$, 那么求解步骤中的一些细节就需要推广到二维空间上.在 $x$ 轴、 $y$ 轴上的计算区间内分别取等间距的 $N$ 个位置 $\mathbf{x}={\left(x_1,x_2,\dots ,x_N\right)}^{\mathrm{T}}$ 以及 $\mathbf{y}={\left(y_1,y_2,\dots ,y_N\right)}^{\mathrm{T}}$, 于是在 $x-y$ 平面上的计算区域内就得到了 $N^2$ 个位置的坐标 $\left(x_1,y_1\right),\left(x_1,y_2\right),\dots ,\left(x_1,y_N\right),\left(x_2,y_1\right),\dots ,\left(x_2,y_N\right),\dots ,\left(x_N,y_N\right)$ .相应地, 函数 $u$ 可以被离散化为 $N$ 阶方阵（第一种形式）或 $N^2$ 维列向量（第二种形式）, 如式 % \eqref{4-28} 、式 % \eqref{4-29} 所示:

$$\begin{array}{rl}& {\mathbf{u}}_{N\times N}=\left(\begin{array}{cccc}{u}_{11}& u_{12}& \cdots & u_{1N}\\ u_{21}& u_{22}& \cdots & u_{2N}\\ ⋮& ⋮& \ddots & ⋮\\ u_{N1}& u_{N2}& \cdots & u_{NN}\end{array}\right)\end{array}$$

$${\mathbf{u}}_{N^2\times \mathbf{l}}={\left(\begin{array}{cccccccccc}{u}_{11},& u_{21},& \dots ,& u_{N1},& u_{12},& u_{22},& \dots ,& u_{N2},& \dots ,& u_{NN}\end{array}\right)}^{\mathrm{T}}$$

式 % \eqref{4-28} 中, 第 $i$ 行 $j$ 列的元素 $u_{ij}$ 对应的坐标是 $\left(x_j,y_i\right)$ .列向量 % \eqref{4-29} 的第 1 到第 $N$个元素对应于式 % \eqref{4-28} 的第 1 列, 第 $N+1$ 到第 $2N$ 个元素对应于式 % \eqref{4-28} 的第 2 列……依此类推. 另外, 可以通过 Matlab 中的 reshape 函数在二者间进行转换.

收敛阶说明

收敛阶定义

$$order=\{\begin{array}{c}{\log }_2[E(\tau )/E(\tau /2)],\text{ in time }\\ {\log }_2[E(N)/E(2N)],\text{ in space. }\end{array}$$

时间方向	空间方向
斜率含义	斜率含义
$$\begin{array}{rl}k& =\frac{{\log }_{2}E(\tau )-{\log }_{2}E\left(\frac{\tau }{2}\right)}{{\log }_2\tau -{\log }_2\frac{\tau }{2}}\\ & =\frac{{\log }_2\frac{E(\tau )}{E\left(\frac{\tau }{2}\right)}}{{\log }_2\frac{\tau }{\frac{\tau }{2}}}\\ & ={\log }_2\frac{E(\tau )}{E\left(\frac{\tau }{2}\right)}\\ & =\text{ order }\end{array}$$	$$\begin{array}{rl}k& =\frac{{\log }_{2}E(N)-{\log }_{2}E\left(2N\right)}{N-2N}\\ & =-\frac{1}{N}{\log }_2\frac{E(N)}{E\left(2N\right)}\\ & =-\frac{1}{N}\text{ order }\end{array}$$
时间步长$\tau$与误差$E(\tau )$的关系	空间剖分$N$与误差$E(N)$的关系
$$\begin{array}{rl}{\log }_{2}E(\tau )& =k{\log }_2\tau +b\\ {\log }_{2}E(\tau )& ={\log }_2{\tau }^k+{\log }_2{2}^b\\ {\log }_{2}E(\tau )& ={\log }_2{2}^b{\tau }^k\\ E(\tau )& =2^b{\tau }^k\end{array}$$	$$\begin{array}{rl}{\log }_{2}E(N)& =kN+b\\ {\log }_{2}E(N)& ={\log }_2{2}^{kN+b}\\ E(N)& =2^{kN+b}\\ E(N)& =2^b{2}^{kN}\end{array}$$