离散数学知识点总结（3）：等值演算，16个命题定律 / 基础等价式，重言式的替换规则，证明有效性和可满足性的方法

等值演算

• 当两个公式具有相同的真值表的时候，我们可以进行等价替换而不对结果的真值产生影响。

Example

$p$	$q$	$p\to q$	$\neg p\vee q$
0	0	1	1
0	1	1	1
1	0	0	0
1	1	1	1

从表格中可以看到 $p\to q$ 和 $\neg p\vee q$ 具有相同的真值表，因此，在任何情况下，这两个合式公式都可以看做是等价的 $\equiv$ 或者 $\iff$，即 $(p\to q)\equiv (\neg p\vee q)$。

Note:

• 命题逻辑的知识点中我们使用两大类符号，一类叫做逻辑联结词 $\neg ,\vee ,\wedge ,\to ,\leftrightarrow$ 他们作用在合式公式的内部。
• 另外一类叫做元语言的符号：$\Rightarrow 或\models$ （蕴含），$\iff 或\equiv$ 等价，这些符号作用在两个 合式公式之间，比如我们上面提到的 “等价” 就代表两个合式公式具有相同的真值。
• 那么上述的两类符号到底有什么联系呢？

$\neg ,\vee ,\wedge ,\to ,\leftrightarrow$ 和 $\Rightarrow 或\models$，$\iff 或\equiv$ 之间的关系

• 假设现在有两个合式公式：$A:p\to q$ 和 $B:\neg p\vee q$ 当我们说 $A\equiv B$ 的时候，我们需要证明 $A\leftrightarrow B$ 是一个 “重言式”，即 $(p\to q)\leftrightarrow (\neg p\vee q)$ 是个重言式。
• 类似地，假设现在有两个合式公式：$A:p\to q$ 和 $B:\neg p\vee q$ 当我们说 $A\Rightarrow B$ 的时候，我们需要证明 $A\to B$ 是一个 “重言式”，即 $(p\to q)\to (\neg p\vee q)$ 是个重言式。

官方定义 $\Rightarrow 或\models$，$\iff 或\equiv$

• 对于一个合式公式 $F$，如果我们对它的命题变元的真值进行指派 （assignment），如果指派的结果使得 $F$ 命题的真值为 $T$，那么我们称这次指派 $\theta$ 是 $F$ 的 model；用符号 $\models$ 来表示
• 如果合式公式 $F$ 的所有 model 都是 合式公式 $G$ 的 model，那么我们称 $G$ 是 $F$ 的一个 “逻辑推论（logical consequence）”，$F\models G$ 或者 $F\Rightarrow G$ 换句话说，如果所有使得 $F$ 成真的指派，也都能保证 $G$ 成真，那么 $G$ 就是 $F$ 的逻辑推论。
• 如果同时满足 $F\models G$ 和 $G\models F$ 那么我们称 $F$ 和 $G$ 具有相同的 models（成真指派），这时候我们也可以说 $F$ 和 $G$ 逻辑等价（logical equivalent）$F\equiv G$

16 个基本等价式 / 命题定律

另一个版本

这个版本里面所有的单条件蕴含都写成了 $\Rightarrow$，其实应该是上一个版本中的 $\to$；所有的双条件蕴含都写成了 $\iff$ ，对应上一个版本中的 $\leftrightarrow$

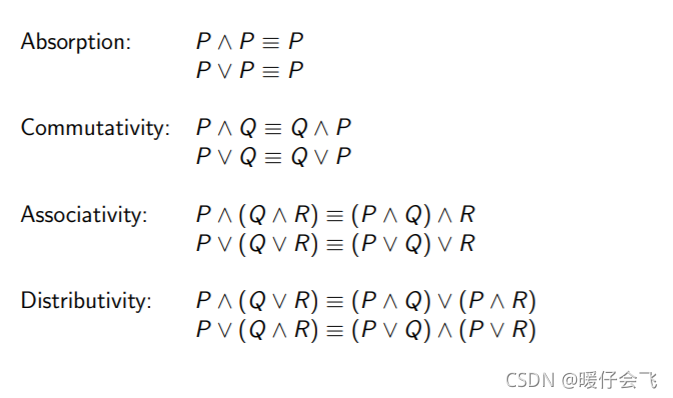
重言式的替换规则

如果一个公式已知是重言式，那么将其内部的变元进行整体替换，得到的还是一个重言式。
例如，已知 $A\vee \neg A$ 是个重言式，那么我将 $A$ 换成任意的变元组合 $(p\to q)\vee \neg (p\to q)$ 依然还是个重言式

证明公式有效性（valid） / 可满足性的（satisfiable）方法

• 如果要证明一个合式公式 $A$ 是 $unsatisfiable$ 的，那么就证明 当且仅当（$iff$） $\neg A$ 是 $valid$。
• 同样的，如果要证明 $A$ 是 $valid$，那么就证明当且仅当 $\neg A$ 是 $unsatisfiable$ 的。