相机标定详解

相机成像原理

小孔成像与像素坐标

小孔成像原理如下图所示（焦点就是等价的小孔）：

我们通常的相机，都是在上图像平面的位置放一块感光板来接收图像，接收到的图像，有一个像素坐标系

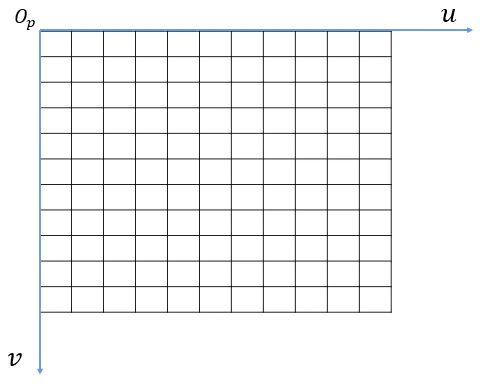
在上图中，任意一个像素点的坐标可以表示为$（u_i,v_i）$。

图像坐标系与相机坐标系

图像坐标系是以图像中心为原点的坐标系，由像素坐标平移得到：

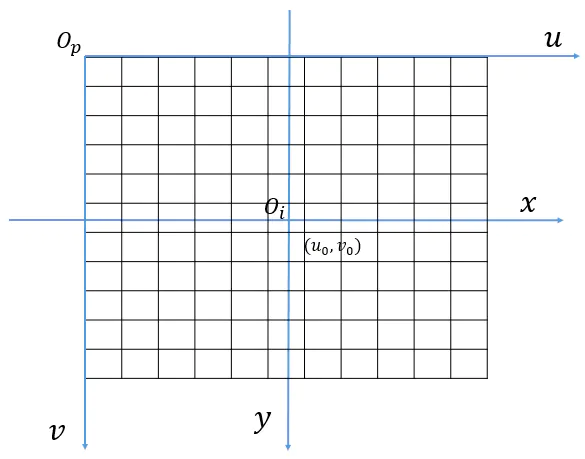
在图中，假设图像中心的像素坐标是$（u_0,v_0）$，相机中感光板每个像素的物理尺寸是$dx\times dy$，那么，图像坐标系的坐标$（x,y）$与像素坐标系的坐标$（u,v）$之间的关系可以表示为：
$$\{\begin{array}{c}x=dx(u-u_0)=u\cdot dx-u_0\cdot dx\\ y=dy(v-v_0)=v\cdot dy-v_0\cdot dy\end{array}$$
改写为矩阵式：
$$\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{cc}dx& 0\\ 0& dy\end{array}\right]\cdot \left[\begin{array}{c}u\\ v\end{array}\right]+\left[\begin{array}{c}-u_0\cdot dx\\ -v_0\cdot dy\end{array}\right]$$
齐次坐标表达：
$$\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{ccc}dx& 0& -u_0\cdot dx\\ 0& dy& -v_0\cdot dy\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}u\\ v\\ 1\end{array}\right]$$

相机坐标系是以相机镜头的焦点为原点的坐标系：

其中焦点到像平面的距离，我们称为像距。对于许多单镜片相机来说，实际上镜片的焦距是固定的，我们只是在调整像距距离，使得物体成像清晰。

作为软件工程师，很多时候我们往往不需要知道像距好焦距的区别，或者说混为一谈，我们只要从小孔成像的角度去分析就可以了，把成像平面对称一下：

然后，我们就把对称过去的虚拟平面到相机坐标的距离称为焦距$f$，（实际上这个距离是物距，为了和其他地方统一，我们后面都称其为焦距）：

由相似三角形原理可得：

$\frac{O_c{O}_i}{O_{c}D}=\frac{O_{c}C}{DA}=\frac{PC}{BA}=\frac{O_{c}C}{O_{c}A}$

把$O_c{O}_i=f$带入，可得实际坐标$(X_c,Y_c)$和图像坐标$(x,y)$的关系：

$\frac{f}{Z_c}=\frac{x}{X_c}=\frac{y}{Y_c}$ ，即： $X_c=x\cdot \frac{Z_c}{f}$，$Y_c=y\cdot \frac{Z_c}{f}$

写成矩阵式如下：
$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{Z_c}{f}& 0& 0\\ 0& \frac{Z_c}{f}& 0\\ 0& 0& Z_c\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$
到此为止，我们只是有了一个成像平面，但是这个平面怎么放，什么角度，什么位置，我们都不知道，像许多工业相机可能会固定安装在特定位置和特定角度：

也就是世界坐标和相机坐标还不一样，我们的相机在现实世界中可以平移，也可以旋转一个角度：

相机坐标与世界坐标的平移变换矩阵为：
$$T=\left[\begin{array}{cccc}1& 0& 0& t_x\\ 0& 1& 0& t_y\\ 0& 0& 1& t_z\\ 0& 0& 0& 1\end{array}\right]$$
绕$x、y、z$轴的旋转变换矩阵分别为:
$$R_x=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& cos\alpha & sin\alpha & 0\\ 0& -sin\alpha & cos\alpha & 0\\ 0& 0& 0& 1\end{array}\right]$$
$$R_y=\left[\begin{array}{cccc}cos\beta & 0& -sin\beta & 0\\ 0& 1& 0& 0\\ sin\beta & 0& cos\beta & 0\\ 0& 0& 0& 1\end{array}\right]$$

$$R_y=\left[\begin{array}{cccc}cos\gamma & sin\gamma & 0& 0\\ -sin\gamma & cos\gamma & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$
可得相机坐标与世界坐标的变换矩阵为
$$\left[\begin{array}{cc}{R}_{xyz}& T_{xyz}\\ 0& 1\end{array}\right]$$
其中:
$R_{xyz}=R_x\cdot R_y\cdot R_z$

$T_{xyz}=\left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]$
所以坐标变换关系即：

$$\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]=\left[\begin{array}{cc}{R}_{xyz}& T_{xyz}\\ 0& 1\end{array}\right]\cdot \left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]$$

相机的内参和外参

通过前面几个步骤，我们可以知道，要把像素坐标变换到世界坐标，需要经历如下步骤：

像素坐标$(u,v)\to$图像坐标$(x,y)\to$相机坐标$(X_c,Y_c,Z_c)\to$世界坐标$(X_w,Y_w,Z_w)$

所谓的内参，指的就是像素坐标$\to$相机坐标的变换参数，
而所谓的外参，即相机坐标$\to$世界坐标的变换参数

外参矩阵与内参矩阵

整体变换的矩阵式如下：
$$\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]=\left[\begin{array}{cc}{R}_{xyz}& T_{xyz}\\ 0& 1\end{array}\right]\left[\begin{array}{ccc}\frac{Z_c}{f}& 0& 0\\ 0& \frac{Z_c}{f}& 0\\ 0& 0& Z_c\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}dx& 0& -u_0\cdot dx\\ 0& dy& -v_0\cdot dy\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}u\\ v\\ 1\end{array}\right]$$

化简可得外参矩阵与内参矩阵：
$$\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]=\left[\begin{array}{cc}{R}_{xyz}& T_{xyz}\\ 0& 1\end{array}\right]\left[\begin{array}{ccc}\frac{Z_c}{f}\cdot dx& 0& -\frac{Z_c{u}_0}{f}\cdot dx\\ 0& \frac{Z_c}{f}\cdot dy& -\frac{Z_c{v}_0}{f}\cdot dy\\ 0& 0& Z_c\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}u\\ v\\ 1\end{array}\right]$$
公式中有一个$Zc$，它表示物体离光学中心的距离。也就是说在标定的时候，如果物体在距离相机的不同位置，那么我们就必须在不同的位置对相机做标定。

齐次坐标与向量的区别

我们在图形学或者很多其他领域内，都会见到齐次坐标的身影，我们会用齐次坐标来表示点，由或者表示向量：
$$P=\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]，\vec{P}=\left[\begin{array}{c}x\\ y\\ 0\end{array}\right]$$
我们会发现，对于向量，底下是用0，对于点，底下是用1，为什么这么规定呢？原因其实很简单，我们对一个向量进行平移，其大小和方向都不会改变，而对于一个点来说，其位置就改变了。假设有如下平移矩阵A，分别对点和向量进行运算，我们很容易从结果看出，点发生了变化，而向量不变：
$$\left[\begin{array}{c}x+t_x\\ y+t_y\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=A\cdot P$$
$$\left[\begin{array}{c}x\\ y\\ 0\end{array}\right]=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ 0\end{array}\right]=A\cdot \vec{P}$$

图像畸变与矫正

造成图像畸变的原因有很多，总结起来可以分为两类：径向畸变和切向畸变。

径向畸变及其矫正

对于透镜而言，以透镜的中心作为原点，往外是透镜的半径的方向，当光线越靠近中心的位置，畸变越小，沿着半径方向远离中心的时候，畸变越大。我们可以用正常同心圆来看他们的变形情况

实际上，也就是两种情况，随着离中心越远距离d越大或者越小

我们可以在线性函数的基础上，通过添加二次项来逼近变形曲线：

即公式如下所示：
$x_2=x(1+k_{1}m+k_2{m}^2+k_3{m}^3)$
$y_2=y(1+k_{1}m+k_2{m}^2+k_3{m}^3)$

其中$（x,y）$是畸变的坐标，$（x_2,y_2）$是矫正后像素点的坐标，且 $m=r^2=x^2+y^2$

我们也可以改写为增量式，把增加量单独分离出来：
$x_2=x+x_{dr}$
$y_2=y+y_{dr}$

其中，增量为：
$x_{dr}=x(k_{1}m+k_2{m}^2+k_3{m}^3)$
$y_{dr}=y(k_{1}m+k_2{m}^2+k_3{m}^3)$

切向畸变及其矫正

咋一看，你会说，那个无夹角切向畸变不是在直径方向有变化么，怎么就切向了，不应该是径向畸变么，实际上我们这里讲的切向，不是指图像的切向，是指呈像的感光元件和透镜存在一个夹角，这个在下面区别中有介绍，这边作为结论记住就可以了。
旋转=放缩+剪切
我们先来看旋转矩阵，并把它分解为放缩+剪切形式：
$\left[\begin{array}{cc}sin\theta & cos\theta \\ -cos\theta & sin\theta \end{array}\right]=\left[\begin{array}{cc}sin\theta & 0\\ 0& sin\theta \end{array}\right]+\left[\begin{array}{cc}0& cos\theta \\ -cos\theta & 0\end{array}\right]$

对一个点进行旋转：
$\left[\begin{array}{cc}sin\theta & cos\theta \\ -cos\theta & sin\theta \end{array}\right]\cdot \left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}sin\theta \cdot x\\ sin\theta \cdot y\end{array}\right]+\left[\begin{array}{c}cos\theta \cdot y\\ -cos\theta \cdot x\end{array}\right]$

可得剪切矫正量：
$$\begin{gathered} dx=cos\theta \cdot y=a_1\cdot y \\ dy=-cos\theta \cdot x=a_2\cdot x \end{gathered}$$

矫正公式：
$x_2=x(1+2p_{1}y+p_2(m/x+2x))$
$y_2=y(1+2p_{2}x+p_1(m/y+2y))$

其中$（x,y）$是畸变的坐标，$（x_2,y_2）$是矫正后像素点的坐标，且 $m=r^2=x^2+y^2$

我们也可以改写为增量式，把增加量单独分离出来：

$x_2=x+x_{dq}$
$y_2=y+y_{dq}$

其中，增量为：
$x_{dq}=2(p_{1}xy+p_2(m/2+x^2))$
$y_{dq}=2(p_{2}xy+p_1(m/2+y^2))$

径向畸变与切向畸变的区别

对于一个相机来说，如果两个方向的变化比例是相等的，则发生径向畸变，若是两个方向变化比例不等，则发生的是切向畸变。我们现在的相机基本上都是径向畸变，切向畸变并不明显。

对于一个透镜而言，一般来说透镜本身四周的曲率都是相等的，也就是两个方向比例变化会相等。但我们还需要考虑呈像板，如果呈像板和透镜是平行的，自然所呈的像也是两个方向变化比例相等（同心圆形），即只发生径向畸变。若是呈像板和透镜不平行，两个方向就会出现比例不一致的情况（椭圆形），并且此时可能还会有一个偏角，即只发生切向畸变。

切向畸变好径向畸变只会发生其中一个，不可能同时发生，所以畸变矫正公式可以写成如下形式：
$x_2=x+x_{dq}+x_{dr}$
$y_2=y+y_{dq}+y_{dr}$