常用不等式与放缩

1.均值不等式

绝对值不等式

|a|−|b|<=|a±b|<=|a|+|b|

琴生不等式

凸函数：
设 f(x)f(x) 在区间 I 上有定义，如果对任意 x1,x2∈Ix1,x2∈I 和实数 λ∈(0,1)λ∈(0,1) 总有
f(λx1+(1−λ)x2)<=λf(x1)+(1−λ)f(x2)

f(λx1+(1−λ)x2)<=λf(x1)+(1−λ)f(x2)
成立，则称 f(x)f(x) 在区间 I 上为下凸函数
变形：
f(x1)f(x2)⋯f(xn)>=f(x1+x2+⋯+xnn)
f(x1)f(x2)⋯f(xn)>=f(x1+x2+⋯+xnn)

琴生不等式：
若 f 为 [a,b] 上的凸函数，则对任意 xi∈[a,b],λi>0,∑ni=1λi=1xi∈[a,b],λi>0,∑i=1nλi=1,有

伯努利不等式

对实数 x>−1x>−1
当 n>=1n>=1,有 (1+x)n>=1+nx(1+x)n>=1+nx
当 0<=n<=10<=n<=1，有 (1+x)n<=1+nx(1+x)n<=1+nx
当且仅当 n=0,1n=0,1 或 x=0x=0 时等号成立
一般式：
(1+x1+x2+x3+⋯+xn)<=(1+x1)(1+x2)(1+x3)⋯(1+xn)

柯西不等式

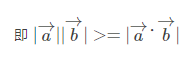
排序不等式

若数列 {an}、{bn} 满足单调不下降，则有：顺序和 >= 乱序和 >= 逆序和

切比雪夫不等式

放缩