swap-test电路分析（输入为混合态）

前言

1.输入均为纯态
2.输入一个为纯态、一个为混合态
3.输入均为混合态

预备知识：

1. 混合态和纯态的回顾请参考《关于纯态、混合态的个人理解》

2. 纯化请参考《施密特分解与纯化》

3. 不同状态下，迹和内积的关系：

1.两个量子态均为纯态

（1）电路图

2. 输入为纯态和混合态

1. （1）电路图

用|0>测得0的概率：$P0=1/2(1+<\phi |\rho |\phi >)$
用|1>测得1的概率：$P1=1/2(1-<\phi |\rho |\phi >)$

2. （2）例子：

现有混合态:

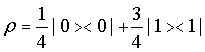
纯化（加粗部分为为了进行纯化添加的标准正交基）

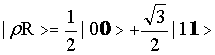
现有纯态（注意要进行归一化~)

(1)初始量子态

(2)经过H门

(3)经过C-SWAP 门

(4)经过H门

(5) 用|0>测得0的概率：

3. 输入均为混合态

1. （1）电路图
   

用|0>测得0的概率：$P0=1/2(1+tr(\rho \sigma ))$
用|1>测得1的概率：$P1=1/2(1-tr(\rho \sigma ))$

下面举个例子,两个混合态：

$\rho =1/4|0><0|+3/4|1><1|$
$\sigma =1/2|0><0|+1/2|0><0|$

纯化得到：

其中第2个qubit,是添加了用于纯化的|iR>(标准正交基)

(1) 初态（2）经过H门：

（3）经过CSWAP门：

这里需要说明的是，我们添加的用于纯化的两个比特不进行CSWAP操作。

（4）经过H门

（5）用|0>求得0的概率：P0=3/4