机器学习基础篇（十一）——主成分分析法

机器学习基础篇（十一）——主成分分析法

一、简介

当我们对含有多个变量的数据进行观测时，我们会收集大量的数据然后分析他们。大样本的数据集固然提供了丰富的信息，但是在一定程度上增加了问题的复杂性。
如果我们分别对每个指标进行分析，往往得到的结论是孤立的，并不能完全利用数据蕴含的信息。但是盲目的去减少我们分析的指标，又会损失很多有用的信息。所以我们需要找到一种合适的方法，一方面可以减少分析指标，另一方面尽量减少原指标信息的损失。
由于不同的指标中存在着相关关系，所以我们可以考虑将关系紧密的指标合成一些新的变量，使得新变量不相关。这样我们就可以用较少的指标来代表存在各个变量中的数据信息。
如图所示：可以将图中的数据集沿着不同的方向，变成新的变量。

二、降维

降维有两种方法，一种是特征消除，另一种是特征提取
特征消除：将会在直接消除那些我们觉得不重要的特征，这会使我们对视这些特征中的很多信息。
特征提取：通过组合现有特征来创建新变量，可以尽量保存特征中存在的信息
PCA（主成分分析）就是一种常见的特征提取方法，PCA会将关系紧密的变量变成尽可能少的新变量，使这些新变量是两两不相关的，于是就可以用较少的综合指标分别代表存在于各个变量中的各类信息。

三、PCA示例

让我们考虑下面的数据集，如图所示：

这里我们可以看到两个向量，分别用红色和绿色来表示。显然可以看出，红色向量对数据的影响更大，主成分分析法将在常规正交坐标系(我们看到的)的变量通过矩阵变换操作映射到另一个正交坐标系中，如图所示：

这样，我们就忽略了一个对我们模型不太重要的特征（绿色）。就可以将二维的数据映射到一维数据中，也就是红色所对应的向量。

四、PCA算法的数学基础

（PCA算法的数据基础为附加知识，没兴趣的同学可以不看，不影响后续学习）
假设我们有M条数据，每个数据有N个特征，被称为样本集X。那么：

对于矩阵X而言，其协方差矩阵为：（协方差矩阵的计算方法可以自行查阅资料，在此不作赘述）

显然矩阵C为一个实对称矩阵，由实对称矩阵的定理可知，对于矩阵C，可以得到以下公式：

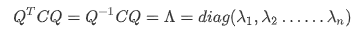
其中C为N阶的实对称矩阵，Q为C的特征向量所组成的正交特征矩阵，Λ为一个对角矩阵。
特征矩阵X中可能存在很多冗余的信息，那么现在我们将其映射到另外一个特征空间中，于是我们得到了矩阵Z：

Z的协方差矩阵为：

可以发现Z的协方差矩阵也为一个对角矩阵，对角线的值是方差，其余值是协方差，为0，代表向量正交。
我们将特征空间转换的过程写作Z = XU，代入矩阵D，可知：
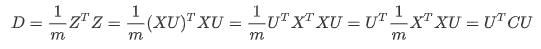也就是说 U = Q ，U 就是矩阵 C 特征向量所组成的矩阵，矩阵 D 对角线上每个值就是矩阵 C 的特征值。

五、主成分数目

在上面的示例中，我们将二维的数据转缩小成了一维的数据。但是在大部分时候，我们最终所得到的因子都是超过两个的。PCA的方法可以用来删除单个特征，也可以减少多个特征。我们有一些策略来帮助我们去判断该减少多少特征：

1. 随机
   我们只需要选择一个合适的特征数目即可，这种方法高度依赖于数据集本身的特征以及我们想要分析的内容是什么 。
   例如在二维平面内将多维数据进行可视化是非常有用的，那么我们只需要将多维的数据逐渐缩小，直至成为二维数据为止。
2. 累计变异的百分比
   我们通过计算每个成分因子能够解释原始数据变异的百分比，然后将不同成分因子所能解释的变异百分比相加，我们就得到了一个值，被称之为累积变异百分比。
   在PCA的过程中，我们将选择能使得这个值最接近于1的维度个数，如图所示：
   
   显然可以看出，随着成分数目的增加，累积变异百分比逐渐增加。当我们需要累积变异百分比大于0.8时，我们至少需要6个主成分因子。通常不建议使得累积百分比等于1，这将会导致有些主成分带来冗余信息。
3. 变异的百分比
   我们通过计算每个成分因子能够解释原始数据变异的百分比。如上图所示，我们也可以选择三个成分。 因为当我们增加第四个主成分因子时，会发现其变异的百分比很小。而且增加它对于累积变异的百分比没有太大的影响，只有略微的增加。
   如果我们把 D 中的特征值按照从大到小，将特征向量从左到右进行排序。然后取其中前 k 个，经过转换（Z = XU），就得到了我们降维之后的数据矩阵 Z。
   这样我们就成功的把N维数据降低到了K维，如下所示
   

六、代码展示

# 主成分分析
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np
#解决中文显示问题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 选择一个随机数种子值，可以让我们最终都显示相同的结果
# 可以选择更改为任何大于0的值，查看不同的随机值结果
# 我们正在使用随机种子，因此我们可以获得相同的结果
seed=9000
seeded_state=np.random.RandomState(seed=seed)
# 用高斯分布随机返回150个二维数据（x,y）,分布大多接近均值，当然也有异常值，高斯分布就是正态分布
rand_points=seeded_state.randn(150,2)
# 我们用@作为矩阵乘法，使得我们的高斯分布更加紧密
points=rand_points @ seeded_state.rand(2,2)
x=points[:,0]
y=points[:,1]
# 现在我们拥有了150个样本用以作为PCA的数据集，画图展示它们
plt.scatter(x,y,alpha=.5)
plt.title('示例数据集')
print('正在绘制数据集..\n')
print('数据集的点：')
for p in points[:10,:]:
    print("({:7.4f},{:7.4f})".format(p[0],p[1]))
print('...\n')
plt.show()

运行结果

# 从给定的数据集里找出两个主成分
pca=PCA(n_components=2)
pca.fit(points)
# 画出所有的图
plt.scatter(x,y,alpha=.5)
plt.title('示例数据集的主成分线条')
# 绘制主成分的线条
for var,component in zip(pca.explained_variance_,pca.components_):
    plt.annotate(
        "",
        component*np.sqrt(var)*2+pca.mean_,
        pca.mean_,
        arrowprops={
            'arrowstyle':"->",
            "linewidth":2
        }
    )
print("正在绘制我们计算的主成分...\n")
plt.show()

运行结果

七、小结

PCA算法是一种具有高度灵活性的机器学习算法。它在分析大量相关数据方面非常具有价值。我们可以任意的选择成分数目，也可以经过自动分析，得出主成分数目。
自学自用，希望可以和大家积极沟通交流，小伙伴们加油鸭。创作不易，动起可爱的双手，来个赞再走呗 (๑◕ܫ￩๑)