本原多项式 M序列和AES不可约多项式

最新推荐文章于 2024-04-21 19:26:19 发布
最新推荐文章于 2024-04-21 19:26:19 发布
阅读量1.6w 收藏 24
点赞数 5
分类专栏： 信息安全 文章标签： 本原多项式 AES 密码学
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_43371004/article/details/85219056
版权

密码学本原多项式

1.本原多项式是近世代数中的一个概念，是唯一分解整环上满足所有系数的最大公因数为1的多项式。本原多项式不等于零，与本原多项式相伴的多项式仍为本原多项式
2.高斯引理：本原多项式的乘积还是本原多项式。

如图:

代数式系数对应的0 1 字串,满足,用8进制变为对应的十进制,若为素数,则为本原多项式此处有错误：不能用素数判断
以下列出几个本原多项式。

此图有错误：
我也是被人误导了，下图中有些数据有错误，还有不应该用是否为素数来判断多项式为本原多项式。

在这里插入图片描述

正确的图（以书为主）：
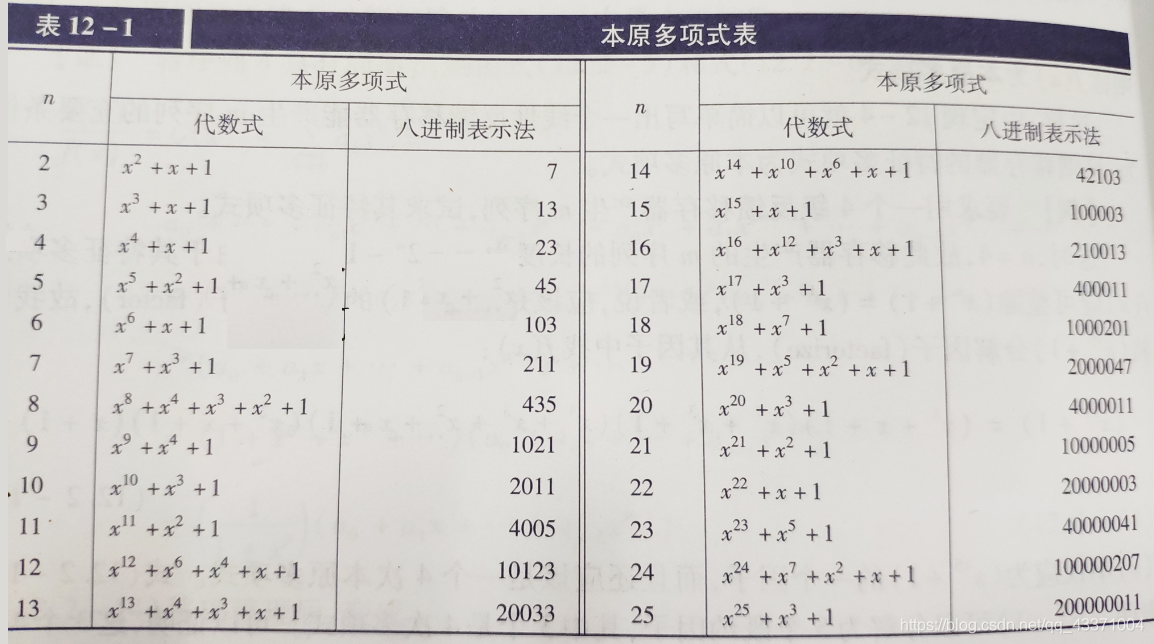
在这里插入图片描述

AES密码学不可约多项式:

不可约多项式和本原多项式不同。

m(x)=(x8+x4+x3+x+1)这个是密码学AES算法查S盒时用到的不可约多项式

公式:y=Ax-1+b
在这里插入图片描述

这里给出S盒中的一部分
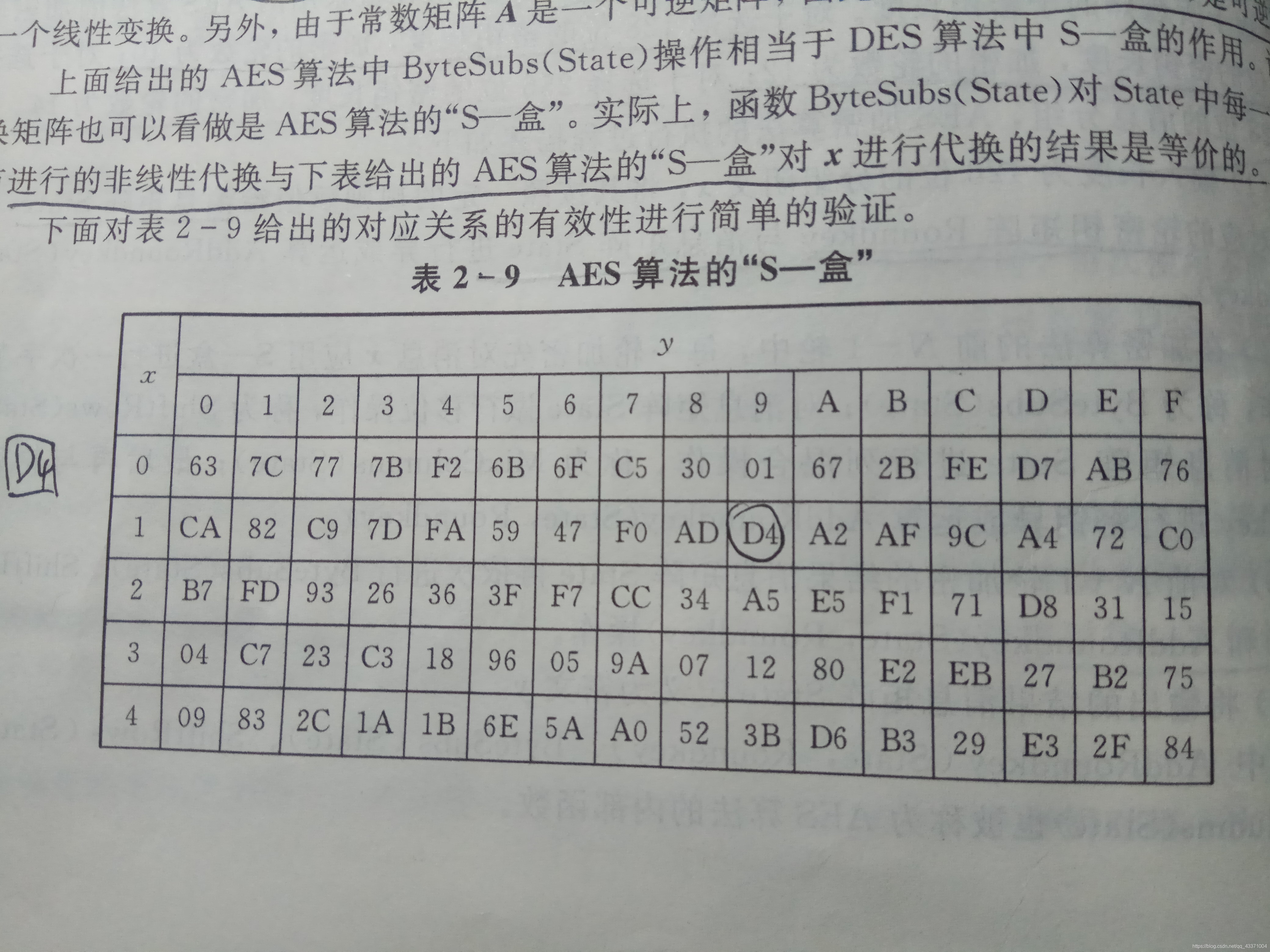
在这里插入图片描述

若给出x = 00001001,想要得到y?
方法一:
x转化成为16进制数字为x=09
查表可以得到x对应的y=01

方法二:
将00001001写为多项式为x3+1
求出(x3+1)-1mod(m(x))的逆元后
即为x6+x3+x2+x+1
转化为2进制即为01001111
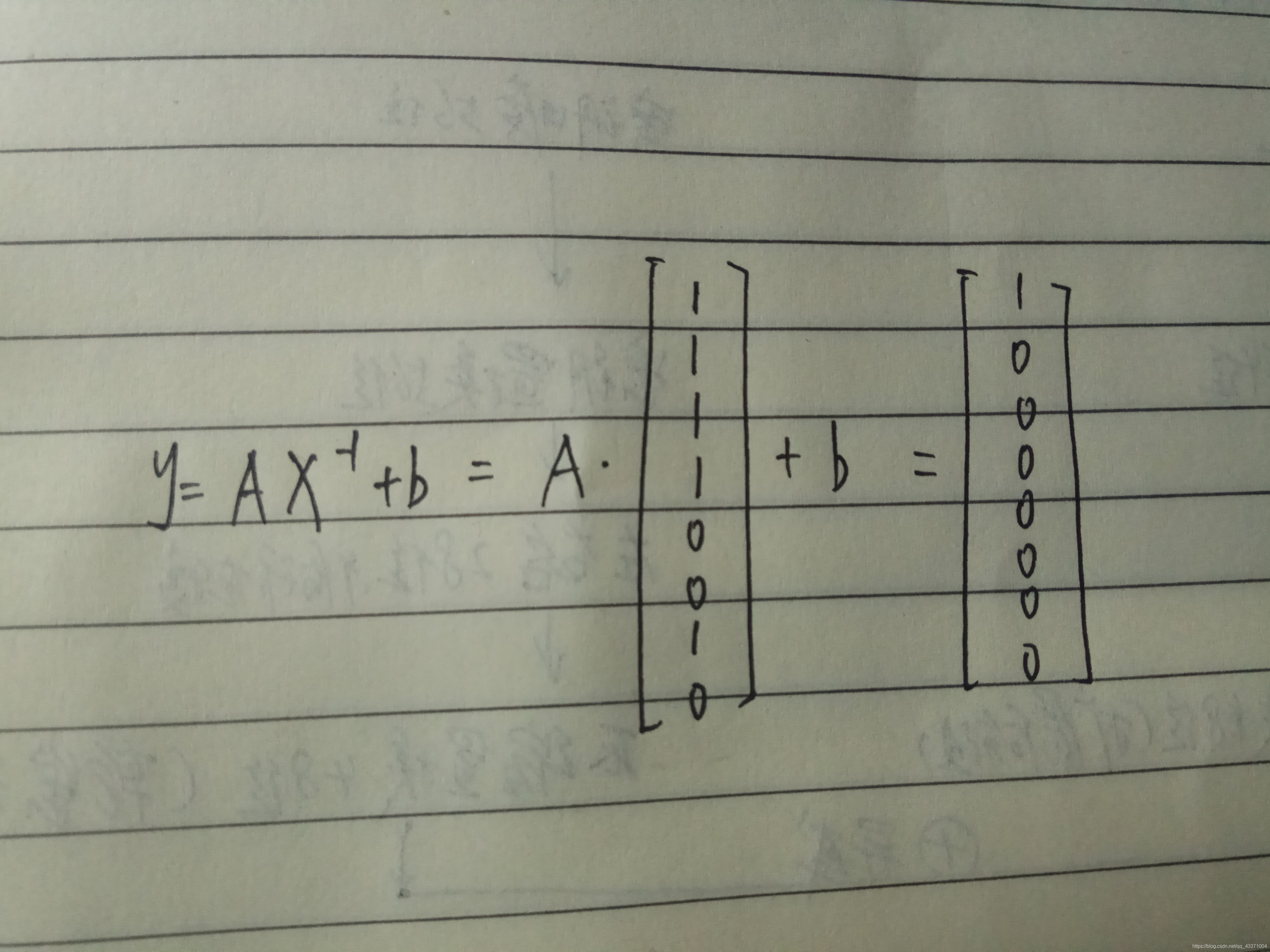
在这里插入图片描述
高位在下,低位在上,利用公式得出00000001,即y=01

谢谢!

当当和嘟嘟
关注
  • 5
    点赞
  • 踩
  • 24
    收藏
    觉得还不错? 一键收藏
  • 7
    评论
专栏目录
密码学系列1-安全规约
qq_41359358的博客
04-22 197
本篇介绍了安全性规约的概念，双线性映射，常见困难性问题（离散对数，CDH,DDH，BDH）。 一、大家初看密码方案的时候，一定迷惑于为什么论文用大篇幅进行安全性证明。为什么需要证明安全性呢？ 比如一个加密方案，若定义安全性为敌手得不到完整密文，那么敌手就很有可能有能力得到部分密文。而安全的加密方案应该使得敌手得不到任何有用的消息。利用安全性规约，我们能够很优雅、规范、严谨地证明我们方案能够达到的安全性。 二、通常是将我们的方案归约到某一个公认的困难性问题上（如离散对数等）.证明思路是如果存在算法攻破我们
GF(2)上的本原多项式
11-16
列出了GF(2)上的不同幂次的本原多项式，可用于构造m序列。
本源多项式生成（原创java，可直接引用，由于二维码里面要运用又不想查表，于是自己手动写了个类，自动生成）
qq_40523239的博客
06-08 1275
1、首先了解本源多项式定义： 二、一个例子 三、 * 比如我们要求Gf(2)上的m次扩展的本原元n=2^m-1 * 那么它的充要条件是此多项式（f(x)）最高项为m次，f(x)为不可约多项式,f(x)能被x^n+1 整除 (f(x|x^n+1)) * 那么f(x)不能被x^q+1整除 1<=q<n * * 得出结论：1。f(x)的最高次项必为m次并且系数为1 * 2.f(x)为不可约多项式必不被x整除 也就是最后一项必须有...
CRC多项式转换二进制
chenyu_Yang的博客
02-28 498
发送方的接收方的约定的一个二进制数；在发送方，利用生成多项式对信息多项式做模2除生成校验码，在接收方，利用生成多项式对收到的编码多项式做模2除检测和确定错误位置。X的最高次幂对应二进制的最高位数；以下各位对应多项式的各幂次，有幂次对应1，无幂次对应0；X的最高次幂是R，转换对应的二进制数R+1位；b、当被传送信息（CRC码）任何一位发生错误时，被生成多项式做模2除后应该使余数不为0。应满足：a、生成多项式的最高位和最低位必须为1。c、不同位发生错误时，应该使余数不同。d、对余数继续做模2除，应使余数循环。
m序列
weixin_34324081的博客
11-04 1601
产生m序列移位寄存器是一种逻辑电路，1阶，2阶...的电路图各不相同。 一般使用本原多项式计算出各阶数电路图。 一般的多项式为 f(x) = c0 * x^0 + c1 * x^1 + c2 * x^2 + c3 * x^4 ... 则4阶本原多项式 f(x) = 1 + x + x^4 = 1 * x^0 + 1 * x^1 + 0 * x^2 + 0 * ...
数学——本原多项式
lwhaaaa的博客
08-18 2万+
本原多项式定义 一个 m 阶的不可约多项式 f(x)\large f(x)f(x)，如果 f(x)\large f(x)f(x) 整除 xn+1\large x^n+ 1xn+1 的最小正整数 n 满足 n=2m−1\large n=2^m-1n=2m−1 ，则该多项式是本原的。 参考定义（百度上的定义）： 设 f(x)=a0+a1x+a2x2+⋯+anxn\large f(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^nf(x)=a0​+a1​x+a2​x2+⋯+an​xn是唯一分解整环D
特征多项式生成M序列
11-21
根据特征多项式得到对应的m序列，特征多项式的输入为matlab通用的多项式输入方式。返回一个m序列。
不同周期m序列（伪随机序列）的matlab详细生成方法
慢慢前行中的博客
08-19 1万+
不同周期m序列的matlab详细生成方法 m序列是由线性反馈移存器产生的伪随机序列，而线性反馈移存器产生m序列的充要条件为：其特征多项式为本原多项式。只要找到本原多项式，就能由它构成m序列。但本原多项式的寻找并不简单，这里给出了经过前人大量计算整理得出的本原多项式表；通过给定的本原多项式，再调用后面的m_sequence函数，即可生成对应周期的m序列。 调用 clear; clc; fbconn...
常用本原多项式
皮哥的技术专栏
11-27 1万+
分享一下常用的原本多项式：
m序列原理和simulink和verilog实现
weixin_47032674的博客
06-03 4222
m序列原理和simulink和verilog实现
m序列产生原理及其性质
热门推荐
kinsun
05-06 12万+
m序列产生原理及其性质 一、m序列的简介 1、m序列是最长线性移位寄存器序列的简称。顾名思义，m序列是由多级移位寄存器或其延迟元件通过线性反馈产生的最长的码序列。在二进制移位寄存器中，若n为移位寄存器的级数，n级移位寄存器共有 2n 个状态，除去全0状态外还剩下 2n-1 中状态，因此它能产生的最大长度的码序列为 2n-1 位，也就是说，一个n级线性反馈移位寄存器产生的最长周期等于 2n-1 ...
matlab仿真产生m序列,基于Matlab的m序列的产生和相关性能仿真
weixin_39579468的博客
03-19 1392
9 电子技术研发 Electronics R & D 了本原多项式，就能由它构造m序列产生器。f(x)的倒量 就是所产生的m序列，这个m序列各位的取值按f(x)式中各项的幂次自低至高取它们的系数。经过前人大量的计算，已将本原多项式列表备查，表1给出了部分本原多项式。由于本原多项式的逆多项式(即把系数倒转)也是本原多项式，所以表中对应的一个数有两个特征多项式。 表1 部分本原多项式 2 m序...
mseq.rar_mseq_mseq.m_m序列 多项式_本原多项式
09-24
m序列生成程序，不同阶数、本原多项式等。。
M序列最下本原多项式
09-23
详细介绍了M序列本原多项式公式和连接方法
里德-所罗门本原多项式生成 C代码
11-02
1、RS编译码本原多项式生成C代码，简单易懂得，含调试代码 2、编写环境Ubuntu12.04 3、包含简易Makefile、原代码
PN 序列生成：生成长度为 31 的 m 序列。-matlab开发
06-01
这个m文件生成了所有长度为31的m序列。为了生成长度为31的m序列，我们使用5次原始多项式。5次原始多项式有3个，所以会有3个不同的m序列长度 31。
密码学 | 承诺：绑定性 + 隐藏性
狂放不羁霸的博客
04-20 1082
绑定性和隐藏性的定义和安全性
真实世界的密码学（三）
最新发布
龙哥盟
04-21 847
用户身份验证协议（机器验证人类的协议）通常在安全连接上进行，只有机器（服务器）已经通过验证。在这个意义上，它将单向验证连接升级为双向验证连接。用户认证协议大量使用密码。密码已被证明是一种相对实用的解决方案，并被用户广泛接受。但由于密码卫生不佳、熵值低和密码数据库泄露等问题，密码也导致了许多问题。有两种方法可以避免用户携带多个密码（并可能重复使用密码）：密码管理器—用户可以使用的工具，用于为他们使用的每个应用程序生成和管理强密码。单点登录。
密钥密码学（三）
龙哥盟
04-21 887
这本书介绍了大约 140 种不同的密码，以及无数的变体。这可能会使一些读者困惑。他们可能只想知道一件事：“对我来说什么是最好的密码？”这个问题很复杂，因为这本书是为如此广泛的读者群体而设计的。在这个结语中，我希望提供一些有用的答案。儿童：这里有几种儿童可以理解和使用的密码。他们可以使用简单的替换密码，尤其是凯撒密码。儿童特别喜欢字母被图片或符号替换的密码，比如🙂☽♡⚇⚓🎾🧙☼◈☆。儿童也喜欢路径置换。青少年可能会喜欢列置换和贝拉索密码。爱好者：爱好者可能会喜欢与朋友交换密码，挑战彼此解密。
利用matlab，编写具有菜单页面的m序列生成器，输入移位寄存器阶数和寄存器的初值，根据输入的阶数查表得到本原多项式系数后，输出多项式系数和m序列，其中，1阶的本原多项式系数为7，2阶的本原多项式系数为13，3阶的本原多项式系数为23，4阶的本原多项式系数为45，5阶的本原多项式系数为103,6阶的本原多项式系数为103，7阶的本原多项式系数为211，8阶的本原多项式系数为435，9阶的本原多项式系数为1021，10阶的本原多项式系数为2011，以上本原多项式系数均为八进制
05-25
以下是利用 MATLAB 编写的具有菜单页面的 m 序列生成器代码，可以根据输入的移位寄存器阶数和寄存器的初值生成相应的 m 序列： ```matlab % m序列生成器 clear all; while 1 % 无限循环，直到选择退出 % 菜单页面 fprintf('请选择移位寄存器阶数：\n'); fprintf('1. 1阶\n'); fprintf('2. 2阶\n'); fprintf('3. 3阶\n'); fprintf('4. 4阶\n'); fprintf('5. 5阶\n'); fprintf('6. 6阶\n'); fprintf('7. 7阶\n'); fprintf('8. 8阶\n'); fprintf('9. 9阶\n'); fprintf('10. 10阶\n'); fprintf('0. 退出\n\n'); % 接收用户输入 n = input('请输入选项序号：'); if n == 0 break; % 选择退出，跳出循环 elseif n < 1 || n > 10 fprintf('输入错误，请重新选择！\n\n'); continue; % 输入错误，重新进入循环 end % 根据移位寄存器阶数查表得到本原多项式系数 switch n case 1 p = oct2poly('7'); % 1阶的本原多项式系数为7 case 2 p = oct2poly('15'); % 2阶的本原多项式系数为13 case 3 p = oct2poly('43'); % 3阶的本原多项式系数为23 case 4 p = oct2poly('105'); % 4阶的本原多项式系数为45 case 5 p = oct2poly('207'); % 5阶的本原多项式系数为103 case 6 p = oct2poly('413'); % 6阶的本原多项式系数为203 case 7 p = oct2poly('1005'); % 7阶的本原多项式系数为421 case 8 p = oct2poly('2107'); % 8阶的本原多项式系数为1053 case 9 p = oct2poly('4005'); % 9阶的本原多项式系数为2057 case 10 p = oct2poly('10123'); % 10阶的本原多项式系数为5103 end % 接收用户输入 x = input('请输入移位寄存器的初值（二进制形式）：','s'); l = length(x); % 初始化寄存器 register = zeros(1, n); for i = 1:n register(i) = str2num(x(l-i+1)); end % 生成m序列 m = zeros(1, 2^n-1); for i = 1:2^n-1 m(i) = register(n); feedback = mod(sum(register.*p), 2); % 计算反馈 register(2:n) = register(1:n-1); % 移位 register(1) = feedback; % 更新最低位 end % 输出多项式系数和m序列 fprintf('多项式系数为：'); disp(p); fprintf('m序列为：'); disp(m); fprintf('\n'); end ``` 上述代码中，我们利用了 MATLAB 自带的 `input` 函数接收用户输入，利用 `switch` 语句根据输入的移位寄存器阶数查表得到本原多项式系数，利用 `oct2poly` 函数将八进制转换成多项式系数，然后利用循环生成 m 序列。最后，我们输出多项式系数和 m 序列，然后重新进入循环，等待下一次输入。当用户选择退出时，我们利用 `break` 语句跳出循环，程序结束。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 7
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值