多项式概率分布（Multinomial probability distribution）和分类分布（categorical distribution）

最新推荐文章于 2025-03-24 15:50:45 发布

音程

最新推荐文章于 2025-03-24 15:50:45 发布

阅读量5.3k

点赞数 2

分类专栏：数学文章标签： python 概率论

本文链接：https://blog.csdn.net/qq_43391414/article/details/120614915

版权

数学专栏收录该内容

46 篇文章

订阅专栏

本文介绍了多项式概率分布和分类分布的概念，从二项分布出发，阐述了如何从两种状态推广到多种状态的情况。通过Python的torch库展示了多项分布和分类分布的实战操作，包括进行多次实验并观察不同状态出现的次数。此外，还探讨了分类分布作为多项式分布的特殊情况。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

- - 多项式概率分布
  - 分类分布

多项式概率分布

其由二项分布推广而来，从而更加普遍。所以我们先回顾一下二项分布。

二项分布的典型例子是扔硬币，设硬币正面朝上概率为 $p$ , 重复扔 $n$ 次硬币，记硬币正面朝上的次数为 $X$ ，显然 $X$ 是一个随机变量，且服从二项分布，即 $X\sim B(n,p)$ 。

把二项分布推广至两种以上的状态，就得到了多项分布。

比如做一次实验，结果有k种可能，各自的概率为 $(p_1,\ldots ,p_k)$ ，同样，重复做n次实验，记各种状态出现的次数为 $(X_1,\ldots ,X_k)$ ，显然，这些都是随机变量，且服从多项分布，即 $(X_1,\ldots ,X_k)\sim PN(n：p_1,\ldots ,p_k)$ ，显然有关系： $X_1+\ldots +X_k=n$ ，另外，其中PN即poly nomial的意思，也是多项式的意思。

python实战：

import torch
p=torch.tensor([0.2,0.1,0.7])
torch.multinomial(p,2,replacement=True)#表示进行两次重复实验，各个状态的概率分布是p

我们重复运行两次，得到如下结果：
在这里插入图片描述
上面表示第一次得到了0.2概率的那个状态，第二次得到了0.7概率的那个状态。下面这个同样分析。

分类分布

分类分布（categorical distribution）好简单，就是多项式概率分布的特殊情况，即n=1的时候；另外一个观点就是扩展了的两点分布，也即扩展了的伯努利分布。

import torch
p=torch.tensor([0.2,0.1,0.7])
torch.multinomial(p,1,replacement=True)#取n=1就是分类分布。

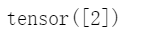
在这里插入图片描述

或者，torch里面有一个专门的分类分布，有兴趣可以看看。

cdis=tdc.Categorical(torch.tensor([0.2,0.1,0.7]))
cdis.sample()

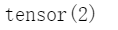
在这里插入图片描述