论文阅读“Understanding dimensional collapse in contrastive self-supervised learning”(ICLR2022)

最新推荐文章于 2023-12-19 15:04:45 发布

不吃香菜的zbw

最新推荐文章于 2023-12-19 15:04:45 发布

阅读量1.4k

点赞数 3

分类专栏：论文阅读文章标签：深度学习计算机视觉人工智能

本文链接：https://blog.csdn.net/qq_43497436/article/details/125205084

版权

论文阅读专栏收录该内容

39 篇文章 11 订阅

订阅专栏

论文标题

Understanding dimensional collapse in contrastive self-supervised learning

论文作者、链接

作者：Jing, Li and Vincent, Pascal and LeCun, Yann and Tian, Yuandong

链接：https://arxiv.org/abs/2110.09348

Introduction逻辑（论文动机&现有工作存在的问题）

自监督学习：目标是在没有人工标注的情况下学习有用的特征表示——琐碎解：模型将所有的输入映射到一个恒定的向量中——常见的避免琐碎解（模型坍塌）的方法有：正\负样本对；利用梯度停止+额外的预测器；额外的聚类步骤；最小化两个分支的冗余——在一些情况下会出现，非完全崩溃：指在某一个特定的维度崩溃，这种情况也称之为维度崩溃——在利用正负样本对的模型中，在推远负样本的过程中会避免维度崩塌，并且可以利用到所有的维度（然而事实是仍然存在维度崩塌的问题）

本文介绍了两种导致崩塌的机制：（1）沿着特征方向，当数据增广引起的方差大于数据分布引起的方差时，权值崩溃（2）即使数据增广的协方差在所有维度上都比数据方差小，但由于权重矩阵在不同层的相互作用，即隐式正则化，权重仍然会崩溃。

论文核心创新点

证明了自监督学习总是收到维度崩塌的影响，即所有嵌入向量都落入一个低维子空间，而不是整个可用嵌入空间

证明了这两个机制导致维度崩塌：（1）沿着特征维度的强增广（2）潜在正则化驱使模型生成低级解

提出了DiretCLR

论文方法

特征崩塌

如图1（a）所示，自监督学习通过最小化嵌入向量之间的距离学习有用的特征。这可能导致如图1（b）所示的崩塌解。对比学习方法通过推远负样本对来避免完全崩塌解。本节将证明，这样的方法只能避免完全崩溃，但是维度崩溃仍然存在。

对带两层MLP投影器的SimCLR模型训练100轮，然后通过收集在验证集的嵌入向量来对维度进行评估。每个嵌入向量的的尺寸是 $d=128$ 。对嵌入层计算一个协方差矩阵 $C \in \mathbb{R}^{d\times d}$ （这里有 $\overline{\mathbf{z}}:=\sum_{i=1}^{N} \mathbf{z}_{i} / N$ ，其中 $N$ 是样本的总数）

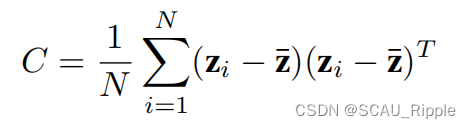
图2展示了该协方差矩阵的奇异值分解 $\left(C=U S V^{T}, S=\operatorname{diag}\left(\sigma^{k}\right)\right)$ 通过对数尺度 $\{\operatorname{log}\left(\sigma^{k}\right)\}$ 进行排序。我们观察到许多奇异值坍缩为零，从而表示坍缩维度。

强力增广导致的维度崩塌

线性模型

在这一节中，解释了一种对比学习的场景，即折叠嵌入维度，其中增广的信息超过输入信息。聚焦于一个简单的线性网络，将输入向量记为 $\bold{x}$ ，然后增广手法是对其增加一些噪音，网络的权值矩阵是 $W$ 。因此，嵌入向量为 $\bold{z}=W\bold{x}$ ，然后使用InfoNCE作为对比损失，即：

其中 $\bold{z}_i$ 和 $\bold{z}_i^\prime$ 是两个分支的嵌入向量， $\bold{z}_j$ 表示负样本。对 $\bold{z}_i$ 和 $\bold{z}_i^\prime$ 进行正则化，使其成为一个统一的向量，可以用内积 $\mathbf{z}_{i}^{T} \mathbf{z}_{i}^{\prime}$ 来代替负距离 $-\left|\mathbf{z}_{i}-\mathbf{z}_{i}^{\prime}\right|^{2} / 2$ 。用不带动量或者是权值减小的随机梯度下降来训练模型。

梯度传播的动力

我们通过梯度流来研究动力，即以无穷小的学习率梯度下降。

引理1：在一个线性对比自监督学习模型中，权重矩阵可以由以下解出：

其中，，并且 $\bold{g}_{z_i}$ 是在嵌入向量 $z_i$ 上的梯度（ $\bold{g}_{z_i^\prime}$ 同理）。

这很容易用链式法则证明。对于InfoNCE损失，每个分支的嵌入向量的梯度可以写成如下：

其中， $\{\alpha_{ij}\}$ 是 $z_i$ 和 $z_j$ 之间的经过softmax之后的相似性，有如下定义：

$\alpha_{i j}=\exp \left(-\left|\mathbf{z}_{i}-\mathbf{z}_{j}\right|^{2} / 2\right) / Z_{i}$

$\alpha_{i i}=\exp \left(-\left|\mathbf{z}_{i}-\mathbf{z}_{i}^{\prime}\right|^{2} / 2\right) / Z_{i}$

$Z_{i}=\sum_{j \neq i} \exp \left(-\left|\mathbf{z}_{i}-\mathbf{z}_{j}\right|^{2} / 2\right)+\exp \left(-\left|\mathbf{z}_{i}-\mathbf{z}_{i}^{\prime}\right|^{2} / 2\right)$

因此， $\sum_{j} \alpha_{i j}=1$ 。又因为有于是有：

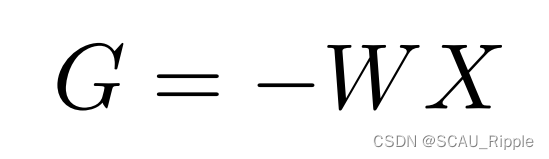
其中

引理2：

$X$ 是两个PSD矩阵的差值（PSD矩阵应该是半正定矩阵，作者好像没讲，我搜索了之后感觉是这样）：

其中，（这两条公式的证明在附录中）

是加权数据分布协方差矩阵

是加权增广分布协方差矩阵

因此增广的幅度决定了X是否是正定矩阵。引理2还将权重 $W$ 的时间导数建模为：a product of $W$ and a symmetric and/or PSD matrices（这句话我实在不知道怎么翻译）。引理2适用于有多个负对比项的InfoNCE，当 $\alpha_{ij}$ 随样本对 $(i,j)$ 变化时仍然成立，在有batch-szie $N$ 下成立

在给定 $X$ 的性质的情况下，研究权矩阵 $W$ 的动力

定理1：一个固定的矩阵 $X$ 和一个强增广，导致矩阵 $X$ 有负的向量值，权值矩阵 $W$ 会有部分奇异值消失。

推论1：（由强增广导致的维度崩塌）在使用强增广的情况下，嵌入空间的协方差矩阵会变成低秩的。

利用嵌入协方差矩阵的奇异值谱识别嵌入空间， $C=\sum_{i}\left(\mathbf{z}_{i}-\overline{\mathbf{z}}\right)\left(\mathbf{z}_{i}-\overline{\mathbf{z}}\right)^{T} / N=\sum_{i} W\left(\mathbf{x}_{i}-\overline{\mathbf{x}}\right)\left(\mathbf{x}_{i}-\overline{\mathbf{x}}\right)^{T} W^{T} / N$ 。由于 $W$ 奇异值消失， $C$ 也是低秩的，表示维数坍缩。

数值模拟验证了我们的理论。我们选择输入数据为：具有协方差矩阵的各向同性高斯数据， $\sum_{i, j}\left(\mathbf{x}_{i}-\mathbf{x}_{j}\right)\left(\mathbf{x}_{i}-\mathbf{x}_{j}\right)^{T} / N=I$ 。选择将增广设置为具有协方差矩阵的加性高斯函数(additive Gaussian)： $\sum_{i}\left(\mathbf{x}_{i}^{\prime}-\mathbf{x}_{i}\right)\left(\mathbf{x}_{i}^{\prime}-\mathbf{x}_{i}\right)^{T} / N=block_diagonal(\mathbf{0}, k * I)$ ，块的大小为8x8。在图3中绘制了不同增幅幅度k的权值矩阵奇异值谱：

这证明了在线性网络的设定下，在嵌入空间中，强增广会导致维度崩塌。

对于复杂的非线性网络，强增广仍然会导致崩塌的情形，但是解释的角度不同。强增广取决于一定网络容量条件下的增广的更复杂性质（增广的高阶统计量，增广与数据分布的流形性）。

潜在归一化导致的维度崩塌

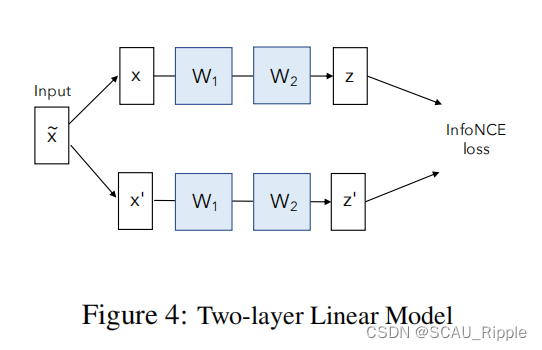
两层线性模型

在强增广的条件下，在InfoNCE损失指导下的线性模型会出现维度崩塌。然而，这种情况下依赖于网络容量是有限的的情况，实际上可能不成立。另一方面，当没有强增广的时候 $\left(\hat{\Sigma}_{1} \prec \hat{\Sigma}_{0}\right)$ ，并且因此 $X$ 矩阵仍然是PSD，一个线性模型也不会出现维度崩塌。然而实际情况下深度神经网络仍然会出现崩塌。下文将从另一个方面揭示：潜在归一化，导致过度参数化的线性模型倾向于找到一个低秩的解。

为了理解这个反直觉的情况，我们先设定一个最简单的过度参数化的设定，将网络设置成为一个2层的MLP并且没有偏置值。这两个MLP的权重矩阵记为 $W_1 \in \mathbb{R}^{d \times d}$ 和 $W_2 \in \mathbb{R}^{d \times d}$ 。输入向量记为 $\bold{x}$ 然后其增广为添加了额外的噪音。于是每个分支输出的嵌入向量为： $\bold{z}=W_1W_2\bold{x}$ ，因此 $\bold{z} \in \mathbb{R}^n$ ，不对 $\bold{z}$ 进行归一化，最后使用InfoNCE作为损失函数。在没有动量或是权重减小的情况下使用随机梯度下降对模型进行训练。

梯度流动力

与引理1相似，推导了两个权矩阵W1和W2上的梯度流。

引理3：引理1中定义了由 $\left(G=\sum_{i}\left(\boldsymbol{g}_{\mathbf{z}_{i}} \boldsymbol{x}_{i}^{T}+\boldsymbol{g}_{\mathbf{z}_{i}^{\prime}} \boldsymbol{x}_{i}^{\prime T}\right)\right)$ 演化的两层线性对比自监督学习模型的权值矩阵:

该式可以用链式法则证明。对于两层的情况，对于 $G$ 有一个具体的形式：

其中 $X$ 由上文中的公式6定义。根据推论2，我们得知，在小增广的情况下， $X=\hat{\Sigma}_{0}-\hat{\Sigma}_{1} \succ 0$ 是一个正定矩阵。

权重对齐

至此我们又了两个矩阵 $W_1$ 和 $W_2$ ，第一个问题是它们如何相互影响。在两个矩阵上都应用SVD分解，即 $W_1=U_1S_1V_1^T$ 和 $W_2=U_2S_2V_2^T$ ，以及 $S_1=diag([\sigma_1^k])$ 和 $S_2=diag([\sigma_2^k])$ 。对齐受到相邻的标准正交矩阵之间的影响，即： $V_2=[\bold{v}_2^k],U_1=[\bold{u}_1^k]$ 。这可以通过对齐矩阵来表示， $A=V_2^TU_1$ ，其中矩阵中的 $(k,k^\prime)$ 实例，代表了第 $k$ 个的 $W_2$ 的右边的奇异值向量 $\bold{v}_2^k$ 和第 $k^\prime$ 的 $W_1$ 的左边的奇异值向量 $\bold{u}_1^{k^\prime}$ 的对齐。

定理2：（权重矩阵对齐）对于所有的 $t$ ，有 $W_2(t)W_1(t) \neq 0$ ， $X(t)$ 是一个正定矩阵，并且 $W_1(+\infty),W_2(+\infty)$ 具有不同的奇异值，那么对齐矩阵有 $A=V_{2}^{T} U_{1} \rightarrow I$

同时，通过实验证明了在InfoNCE损失的指导下，对齐矩阵 $A$ 的绝对值收敛到一个单位矩阵，见图5。

现实情况下很多假设是不成立的，比如权值矩阵中存在退化奇异值，不能做到完美对齐。事实上，给定退化的奇异值，奇异分解不再是唯一的。在实验过程中，人为的将权重矩阵初始化为没有退化奇异值的矩阵。在实际情况下，权重矩阵是随机初始化的，将会观察到权重矩阵收敛到一个分块对角矩阵，其中每一个块代表一组退化的奇异值。

考虑到奇异向量对应于相同奇异值对齐，我们现在可以研究每个权矩阵 $W_1$ 和 $W_2$ 的奇异值的动力

定理3：如果 $W_1,W_2$ 是对齐的（即 $V_2=U_1^T$ ），那么它们的奇异值在InfoNCE损失的影响下演化为：

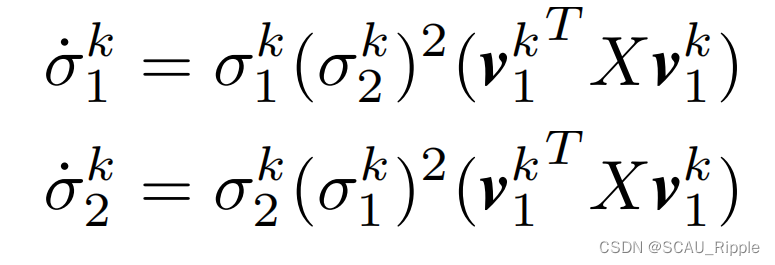
根据公式10，有 $(\sigma _1^k)^2 = (\sigma _2^k)^2 +C$ 。我们用解析法求解奇异值动力， $\sigma_1^k=\sigma_1^k((\sigma_1^k)^2+C)({\bold{v}_1^k}^TX\bold{v}_1^k)$ 。这表示一对奇异值有与自身成比例的梯度。值得注意的是， $X$ 是一个正定矩阵，项 ${\bold{v}_1^k}^TX\bold{v}_1^k$ 是恒为非负的。这解释了为什么我们观察到的最小组的奇异值很明显增长缓慢。由图6（a）的实验证明该点。

推论2：（由潜在归一化导致的维度崩塌）在有小增广和过度参数化的线性模型下，嵌入空间中的协方差矩阵会变成低秩的。

嵌入空间由基于嵌入向量的协方差矩阵的奇异值谱所确定，即 $C=\sum(\mathbf{z}-\overline{\mathbf{z}})(\mathbf{z}-\overline{\mathbf{z}})^{T} / N=\sum W_{2} W_{1}(\mathbf{x}-\overline{\mathbf{x}})(\mathbf{x}-\overline{\mathbf{x}})^{T} W_{1}^{T} W_{2}^{T} / N$ 。随着 $W_2W_1$ 演化为低秩的， $C$ 也变成低秩的，表现为维度崩塌。如图6（c）见实验。

DirectCLR

动机

通过上文的发现去设计一个新颖的算法。根据经验，添加一个投影器大大提高了学习表征的质量和下游任务性能（SimCLR）。检查表示层的光谱也可以发现使用/不使用投影器的差异，见图7（b）。

在没有投影器的时候，模型出现了维度崩塌。因此。投影器避免了在特征空间的崩塌。

投影器在对比学习中，起到了关键的避免维度崩塌的情况。

在对比学习模型中，我们提出以下关于线性投影仪的建议：

建议1：线性投影器的权重矩阵只需要是对角化的。

建议2：线性投影器的权重矩阵只需要是低秩的。

基于潜在归一化的理论，我们希望看见邻接层 $W_1(U_1S_1V_1^T),W_2(U_2S_2V_2^T)$ 进行对齐，使整体动力仅由它们的奇异值 $S_1$ 和 $S_2$ 控制。正交矩阵 $V_2^T$ 和 $U_1$ 是多余的，他们会演化成 $V_2^TU_1=I$ 。

现在考虑SimCLR的线性投影器的通道维度。 $W_1$ 是编码器的最后一层的权重矩阵， $W_2$ 是投影器的权重矩阵。对于投影器矩阵 $W_2$ ，正交分量 $V_2$ 可以省略。因为前一层的 $W_1$ 已经被训练好了，其正交分量 $U_1$ 总是满足 $V_2^TU_1=I$ 。因此，投影仪的最终表现仅由投影仪权值矩阵的奇异值( $S_2$ )决定。于是有了建议1:权矩阵的正交分量不重要。我们可以把投影仪矩阵设为对角矩阵。并且，权重矩阵总是会收敛到低秩。奇异值对角矩阵自然也变成低秩的了，所以为什么不直接将其设置成低秩的呢？于是有了建议2。

主要想法

本文建议去移除对比学习中的投影器，通过直接将特征向量的子向量送到损失函数计算。将模型命名为DirectCLR，见图8。

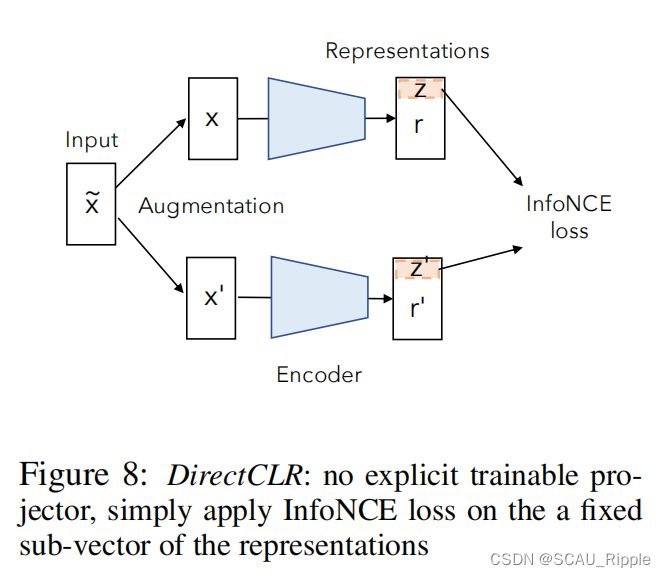
DirectCLR之间选择特征 $\bold{z}=\bold{r}[0:d_0]$ 的一个子向量，其中 $d_0$ 是超参。然后在正则化的子向量上应用InforNCE损失，即 $\hat{\bold{z}}=\bold{z}/|\bold{z}|,=L=\sum_{i} \log \frac{\exp \left(\hat{\mathbf{z}}_{i} \cdot \mathbf{\mathbf { z }}_{i}^{\prime}\right)}{\sum_{j} \exp \left(\hat{\mathbf{z}}_{i} \cdot \hat{\mathbf{z}}_{j}\right)}$ 。

在和SimCLR同等条件下的训练结果：

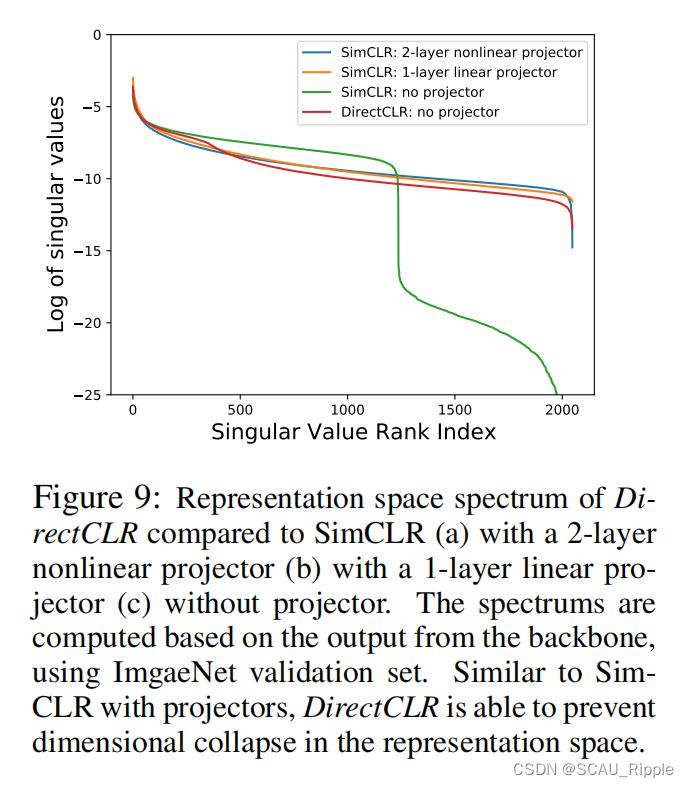
对潜在特征空间的光谱如图9所示。DirectCLR避免了维度崩塌，和带投影器的SimCLR的效果一样。

有人可能会怀疑，在DirectCLR的对比损失不应用梯度的其余部分的表示向量 $\bold{r}[d_0:]$ ，那么为什么这些维度会包含有用的信息?

如图10所示，通过梯度反向传播回来的向量是低秩的，只有前 $d_0$ 个通道维度是非零的。当梯度进入主干网络后，穿过最后的非线性传播块，就变成了满秩的。因此，隐藏层 $\bold{h}$ 收到了所有通道的梯度。注意到 $\bold{h},\bold{r}$ 都是相同的维度，即2048。然后我们考虑前向传播，隐藏层 $\bold{h}$ 通过残差链接直接输入特征向量。因此，表示向量 $\bold{r}[d_0:]$ 的其余部分并不是微不足道的。

免责声明:DirectCLR能够取代线性投影器，并在理解线性投影仪的动力学方面验证两个命题。但我们的理论不能完全解释为什么非线性投影仪能够防止维度坍塌。DirectCLR仍然依赖于非线性投影器的机制来防止维度坍塌，这是由骨干的最后一块有效执行的，如上所述。

消融实验设计

对于投影器的消融

一句话总结

带来了一种不用投影器projector也能防止模型坍塌的新思路

论文好句摘抄（个人向）

不吃香菜的zbw

关注

3
点赞
踩
7

收藏

觉得还不错? 一键收藏
0
评论
论文阅读“Understanding dimensional collapse in contrastive self-supervised learning”(ICLR2022)

Understanding dimensional collapse in contrastive self-supervised learning作者：Jing, Li and Vincent, Pascal and LeCun, Yann and Tian, Yuandong链接：https://arxiv.org/abs/2110.09348自监督学习：目标是在没有人工标注的情况下学习有用的特征表示——琐碎解：模型将所有的输入映射到一个恒定的向量中——常见的避免琐碎解（模型坍塌）的方法有：正\负样本对
复制链接

扫一扫