初等数论三

剩余类和完全剩余系

定理1威尔逊定理

设p是一个素数，则$(p-1)!+1\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}p)$
证明

---

充分性
以下的-1都是在模p意义下的，实际上就是p-1。
我们知道$1\ast 1\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}p),(-1)\ast (-1)\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}p)$，且仅有这两组的逆元与本身相等。
这个很好理解，如果$x^2\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}p)，那么x^2-1\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}p)$，因式分解一下，$(x+1)(x-1)\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}p)$，所以x=1或-1。
然后除了这两个数之外，2…p-2中的每一个数一定有一个对应的逆元，一定不与自己相等，这一点上面证过了，而且如果把取逆元看做一个映射，这就是个双射。$a\ast a^{-1}\equiv 1那么a^{-1}\ast a\equiv 1，所以a=(a^{-1}{)}^{-1}$
，即这两个数互为逆元。

先证对于A中每一个元素a，均存在A中另一个元素b，使得$ab\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}p)$。首先，显然$1\le b\le p-1$。然后，假设$b==1，则ab=a\ne 1$，不成立；再假设$b==p-1，则ab=a\ast (p-1)=ap-a\equiv p-a(modp)$，若$p-a==1的话，须满足a==p-1$，不成立。得证。
再证不同的a对应的b不相同。假设存在两个不同的a对应的b相同，再假设这两个a分别为$a_1，a_2(a_1<a_2)。则有(a_2-a_1)\ast b\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}p)。而(a_2-a_1)、b$均小于p且p为素数，故显然不成立。
如果p是2，结论显然成立，如果p>2，那么p一定是个奇素数，所以2…p-2中恰好有偶数个数，且他们两两配对后的乘积模p都是等于1的，再乘上一个1，再乘上个p-1,即-1，所以$(p-1)!\equiv -1(\mathrm{m}\mathrm{o}\mathrm{d}p)$，当然前提是p是质数。

---

必要性
当p不是素数，那么令p=a*b ，其中1 < a < p-1 ,1 < b < p-1.

(1)若a≠b,

    因为(p-1)!=1*2*...*a*...*b*...*p-1,

    所以(p-1)!≡ 0 (mod a)        

           (p-1)!≡ 0 (mod b)

    可得(p-1)!≡ 0 (mod a*b) ，

          即 (p-1)!≡ 0 (mod p)

    与( p -1 )! ≡ -1 ( mod p )  矛盾

(2)若a=b

    因为(p-1)!=1*2*...*a*...*2a*...*p-1.

    所以(p-1)!≡ 0 (mod a)          

           (p-1)!≡ 0 (mod 2a)

    可得(p-1)!≡ 0 (mod a*2a) => (p-1)!≡ 0 (mod a*a) ，

      即 (p-1)!≡ 0 (mod p)

    与( p -1 )! ≡ -1 ( mod p )  矛盾

因此p只能是素数。

缩系

定义1

在一个模m的剩余类中的数与m互素，再在其中各取一个数组成的集合叫做模m的一组缩系

定义2

欧拉函数$\phi (n)$是一个定义在整数上的函数，值为序列0，1，2，。。。，n-1中与n互素的数的个数。
显然p为素数时，$\phi (p)=p-1$

定理2

模m的一组缩系含有$\phi (m)$个数

定理3

若$a_1,...,a_{\phi (m)}$是$\phi (n)$个与m互素的整数，则其为缩系的充要条件是两两模m不同余

定理4

若（a_i，m）=1，x_i是通过模m的缩系，则a_ix_i也是模m的缩系

定理5 欧拉定理

设$m>1,(a,m)=1,则a^{\phi (m)}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}m)$
证明：根据定理$a^n\equiv b^n(\mathrm{m}\mathrm{o}\mathrm{d}m)$或者如下：

定理6 费马小定理

若p是素数，则$a^p\equiv a(\mathrm{m}\mathrm{o}\mathrm{d}p)$

定理7

设$m_1>0,m_2>0,(m_1,m_2)=1,而x_i,y_j$分别通过模$m_1,m_2$的缩系，则$m_2{x}_i+m_1{y}_j通过模m_1{m}_2$的缩系

推论

若$(m_1,m_2)=1,则\phi (m_1{m}_2)=\phi (m_1)\phi (m_2)$

定理8

设n的标准分解$n=p_1^{{\alpha }_1}{p}_2^{{\alpha }_2}...p_k^{{\alpha }_k}$则$$\phi (n)=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})...(1-\frac{1}{p_k})$$

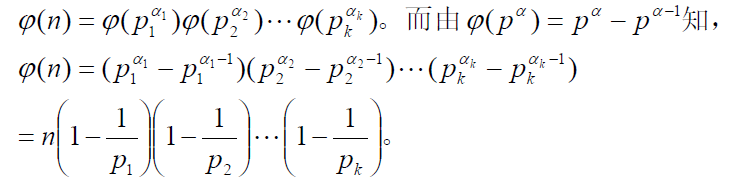
一次同余式

定义3

定理9

设（a,m)=1，m>0,则同余式$ax\equiv b(\mathrm{m}\mathrm{o}\mathrm{d}m)$恰有一个解$x\equiv b{a}^{\phi (m)-1}(\mathrm{m}\mathrm{o}\mathrm{d}m)$，将$ax\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}m)的解a^{\phi (m)-1}$称为a的逆元，记为$a^{-1}$

定理10

设(a,m)=d,m>0，则同余式$ax\equiv b(\mathrm{m}\mathrm{o}\mathrm{d}m)$有解的充要条件是$d\mid b$

定理11

设$(a,m)=d,m>0,d\mid b$,则同余式$ax\equiv b(\mathrm{m}\mathrm{o}\mathrm{d}m)$有d个解。

模是素数的同余式

定理12 拉格朗日定理

设p是素数，$f(x)=a_n{x}^n+a_{n-1}{x}^{n-1}+...+a_{1}x+a_0,n>0,a_n\not\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}p)$最多有n个解。

定理13

定理14