进化是一个慢过程;改变需要时间,但有些类型的改变非常快。变异是几乎所有进化算法都会采用的一种快速变化。
提出反向学习是为了在进化算法中提高学习率。因为,进化是一个慢过程而革命是一个快过程,在进化算法中模拟革命可能会加快算法的收敛。
目录
反向的定义和概念
从标量开始,首先假设x定义在域[a,b]上,并且这个域的中心是c,即
x∈[a,b] 这里a<b,c=(a+b)/2
1.反射反向和模反向
要定义标量x的方向,可以考虑几种不同的方式,例如,x的反射方向定义为
= a + b - x
这意味着和x到域的中心距离相同:
c - x = - c
x的模反向定义为
= (x - a + c) mod(b - a)
反射反向和模反向的定义可以用一种简单直接的方式扩展到向量。假设x是定义在长方形域上的一个n维向量;即,定义在域
上,并且
的域的中心为
:
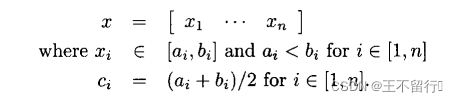
x的反射反向定义为:
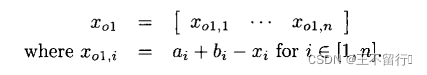
向量x的模反向定义为:
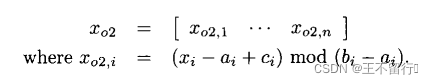
这些定义只适用于长方形域。
接下来的部分我们将“x的反射反向”简称“x的反向”,并将记号 简写为
。
2.部分反向
已知向量x,我们可以定义x的一个部分反向,取x的某些维的反向同时让x的其他元素保持不变。例如:
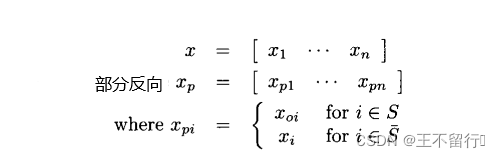
其中S是{1,2,3...,n}的某个子集,是它的补集;即S∪
={1,2,3,...,n},对所有j∈{1,...,|S|},
并且对所有j∈{1,..,|
|},
S,
的反向度定义为
![]()
3.1型反向和2型反向
我们一直用函数的域定义反向,称之为1型反向。也可以用函数的范围定义反向,称之为2型反向。我们从标量x的标量函数y(·)开始,其中x定义在域[a,b]。范围[,
]定义为
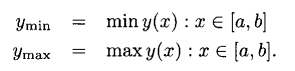
这个范围的中心定义为
![]()
它意味着与y(x)到
的距离相等:
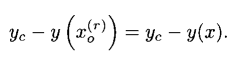
除非y(·)是一一对应的,不然由这个定义可以得到多个 的值。下图说明1型反向和2型反向之间的区别。
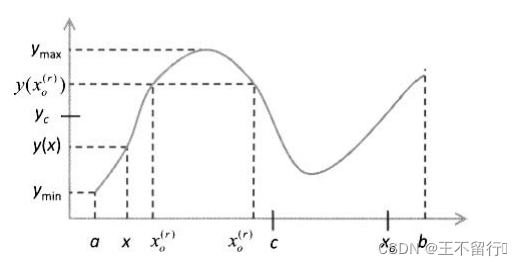
将x反射到中心域c的对面得到x的1型反向。将y(x)反射到域中心
的对面得到
,然后计算
的逆得到x的2型反向
,上图中
有两个可能的值。
接下来的部分只讨论1型反向。
4.准反向和超反向
现在我们定义反向的另外3中方式。与前面一样,考虑标量x∈[a,b],c是域的中心。x的准反向定义如下:
![]()
其中是标准反射反向,即
是均匀分布在[c,
]上的随机数的一个实现。rand函数的结果独立于自变量的顺序,也就是说rand(c,
)和rand(
,c)等价。
x的超反向定义为
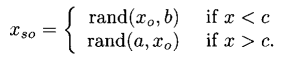
是均匀分布于
和离x最远的域边界之间的随机数的一个实现。这个定义并不完备,因为在c=x的情况下
没有定义,
x的准反射反向定义如下
![]()
是均匀分布于x的c之间的随机数的一个实现。
下图说明反向的4中不同方式。
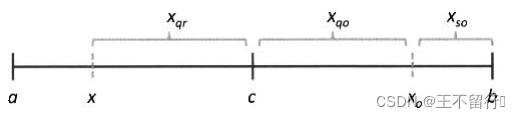
将x反射到域中心c的对面得到x的反向 ;在c和
之间生成一个随机数得到x的准反向
;在
和离x最远的边界之间生成一个随机数得到x的超反向
;在x和c之间生成一个随机数得到x的准反射反向
。
反向进化算法
进化算法使用反向学习的一种简单的方式。
- 当初始化进化算法种群的N个个体时,建立N个反向个体,每个反向个体相应于N个初始个体中的一个。已知2N个候选解(N个初始个体和N个反向),保留最好的N个作为反向进化算法开始的种群。
- 进化算法的标准实现。它涉及费用函数评价、重组,以及变异的循环,按定义每代执行一次循环。
- 每隔几代就计算N个个体各自的反向,在这2N个候选解中(N个标准进化算法的个体以及N个反向个体),为下一代保留最好的N个个体。在每一代依概率
∈[0,1]执行这一步,
被称为跳变率。
是一个可调参数。周期性的生成反向种群是为了探索空间中的未知区域。不想再每一代都生成反向种群,因为那样一来会在搜索空间中反复跳来跳去,浪费函数评价次数。
反向的基于生物地理学优化
将标准BBO算法与反向学习结合就得到反向BBO算法。算法的具体实现如下:
跳变比
跳变比是改进反向学习性能的一个简单扩展。因为反向学习所需的计算资源较多所以提出这个想法。注意,适应性强的个体的反向不大可能比适应性弱的个体的反向强。如果个体靠近最优解,就不值得再去生成它的反向,反之,如果一个个体远离最优解,可能值得生成它的反向。
下述算法是基于适应度的反向逻辑算法,此逻辑可替代反向BBO算法逻辑。参数α>0控制着生成反向个体的压力。与
的适应度成正比,因此,基于适应度的反向逻辑让适应性差的个体更有可能生成反向个体。α越小生成的反向个体越多。当α→0时,基于适应度低的反向逻辑等价与反向BBO算法的标准反向逻辑。α越大生成的反向个体越少。当α→∞时,不生成反向个体,反向BBO算法退化为标准BBO算法。

实施基于适应度的反向逻辑还有另一种方法是只为种群中适应性最差的部分中的个体生成反向个体。它更明确并可以按下面的算法来实施,这里的
∈[0,1]。如果
=1,此逻辑退化为标准反向逻辑。

反向组合优化
对于组合问题,我们想要找到节点排列的最好方式。旅行商问题就是一个很好的例子。假设要用进化算法求解一个4城市旅行商问题。城市标记为ABCD,一个候选解为:
A→B→C→D
- 定义行程的一段为两个相邻城市之间的旅行。上述候选解由三段组成A→B,B→C,C→D。
- 定义两个城市之间的接近度为从一个城市到另一个城市的段的个数。A和B的接近度为1,A和C的接近度为2,A和D的接近度为3.
- 定义一条路的总接近度为每对城市之间接近度的总和。总接近度为3,因为A→B,B→C,C→D每一对的接近度都为1.一条路路径的总接近度总是邓毅N-1,这里N为城市个数。
- 定义路径β的相对接近度为β中每对城市的总接近度和,这里根据某条另外的路径α得到接近度。例如:
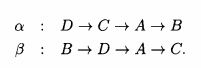
β相对于α的接近度为6.因为β由三段组成:第一段是B→D,在α中这两个城市的接近度为3;第二段是D→A,在α中这两个城市的接近度为2;第三段是A→C,在α中这两个城市的接近度为1.
定义路径α的反向的一种方式是找出相对接近度尽可能大的路径β。α相对于α的相对接近度是N-1,它是可能的最小值。利用这个定义 A→B→C→D的反向为
C→A→D→B
这条相对路径对于A→B→C→D的接近度为7,它是可能的最大值。
要找出相对接近度最大的路径,这本身就是一个组合优化问题。如果用反向学习解决组合优化问题的话,每一代就不得不解决由多个组合问题组成的组合问题。我们定义组合个体的贪婪反向。在贪婪反向中,路径开始的城市不变,然后加入与开始的城市相对接近度最大的城市作为第二个城市。与新的第二个城市相对接近度最大的城市设置为第三个城市。重复这个过程就得到整个贪婪反向路径。下述的算法概述了这个过程:

用上述算法得到 A→B→C→D的贪婪反向为A→D→B→C的接近度为6,比C→A→D→B的接近度少1。下面的算法为实施贪婪反向的另一个更简单的方式。这些算法没有给出旅行商问题候选解的完全反向,但希望它们能以合理的较小的计算代价得到近似反向。

对偶学习
20世纪90年代首次提出对偶学习,在21世纪被重新发现。在反向BBO算法中融入对偶学习的想法就得到下面的算法的对偶逻辑,下面的算法可以替换反向BBO算法的反向逻辑那一段。

在每一代生成对偶的个数可以针对最优的进化算法性能做调整。在每一代执行这个方案,还可以把它添加到上述算法的后面:
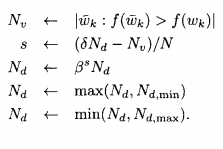
f(·)值较大的个体表示性能较好。是来自前一代的“有效” 对偶个数,有效对偶个数是指由某个个体得到的对偶
比此个体的性能好。参数
∈(0,1)是一个决策阈值。如果有效的对偶的比例大于
,在下一代就生成更多对偶;如果有效对偶的比例小于
,在下一代生成的对偶会更少,β∈(0,1)是控制自适应速度的常数。
和
是
可取的最小值和最大值。
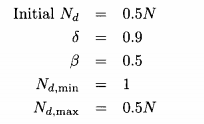
为求解动态优化问题,对偶学习也可以扩展到PBIL。在PBIL中,对偶概率向量与向量p关于50%的概率值对称:
=1-p。





















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








