01背包
我们通过分治把这个问题分解为 当背包容量为0,1,2,3,4。。。时背包容量的最优解
例如
w v w为重量 v为价值
1 2
2 4
3 4
4 5
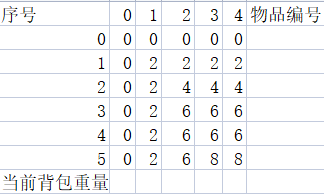
我们可以知道当考虑到dp[2][1]时 当前容量为2 考虑第1个物品 第二个物品为1 2 那么重量1<2 可以被放入 然后再考虑2-1=1 说明此时还可以再放入一个重量为1的物品 那么我们就去dp[1][]找 我们知道我们的思路是分治 所以每一行当考虑完所有物品时就是当前最优解 所以我们会选择dp[N][V]作为答案输出 那么当我们在考虑dp[1][]的时候如果我们选择dp[1][4]也就是这一行最后一个物品的价值时 dp[2][1] = dp[1][4]+2我们会发现其实我们是选择了两次物品一 (1 2)肯定错了
这就是完全背包问题 因为我们不需要考虑物品数量
解决重复选择问题
那我们如何解决物品重复选择问题呢
我们再把问题分治为:
当前背包容量下 且只有0-j个物品时的最优解这样当我们找dp[1][]时应该找的是dp[1][j-1]的值为:
当前背包容量 且只有0-(j-1)个物品时的最优价值+当前物品j的价值
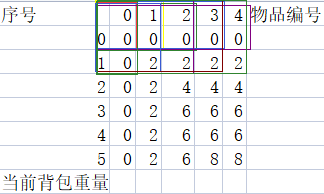
这样考虑
#include<iostream>
#include<bits/stdc++.h>
#include<vector>
#include<stdio.h>
using namespace std;
int main()
{
int N,V;
scanf("%d %d", &N, &V);
vector<vector<int>> dp(V + 1, vector<int>(N+1));
vector<int> w, v;
w.push_back(0);
v.push_back(0);
for (int i = 0; i < N;i++)
{
int x, y;
scanf("%d %d", &x, &y);
w.push_back(x);
v.push_back(y);
}
for (int i = 1; i <= V; i++)//重量
{
for (int j = 1; j <= N; j++)//编号
{
if (i-w[j] >= 0)
{
if (dp[i - w[j]][j - 1] + v[j]>=dp[i][j-1])//核心点在这
{
dp[i][j] = dp[i - w[j]][j - 1] + v[j];
}
else
{
dp[i][j] = dp[i][j-1];
}
}
else
{
dp[i][j] = dp[i][j-1];
}
}
}
printf("%d", dp[V][N]);
return 0;
}
优化为一维
dp[i][j] i为物品序号 j为当前背包重量
因为每次比对是dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])
由此我们可以知道 每一次dp[i][j]只会用到dp[i-1][?]也就是上一行的数据 所以前面的数据就没有必要存储了
而为什么要逆序 也就是
for(int i = 1;i<=N;i++)//这个循环顺序不能改变 因为大循环必须是物品编号i 确保某个编号被遍历过了 就不会重复
{
for(int j = V;j>=w[i];j--)
{
}
}
因为我们知道当我们更新dp[i][j]的时候一定需要j之前的数据也就是
dp[i-1][j-w[i]]
j-w[i]一定比j小 所以我们需要从后往前更新 而未更新的那部分其实就是dp[i-1]那一行的数据
#include<iostream>
#include<bits/stdc++.h>
#include<vector>
#include<stdio.h>
using namespace std;
int main()
{
int N,V;
scanf("%d %d", &N, &V);
int dp[1020] = {0};
vector<int> w, v;
w.push_back(0);
v.push_back(0);
for (int i = 0; i < N;i++)
{
int x, y;
scanf("%d %d", &x, &y);
w.push_back(x);
v.push_back(y);
}
for (int i = 1; i <= N; i++)//编号
{
for (int j = V; j >= w[i]; j--)//重量
{
dp[j] = max(dp[j],dp[j-w[i]]+v[i]);
//因为dp[j]在更新之前就可以看做原来的dp[i-1][j]
}
}
printf("%d", dp[V]);
return 0;
}
python
N,V = map(int,input().split())
w = [0 for i in range(N+1)]
v = [0 for i in range(N+1)]
dp = [0 for i in range(V+1)]
for i in range(N):
w[i+1],v[i+1] = map(int,input().split())
for i in range(1,N+1):
for j in range(V,w[i]-1,-1):
dp[j] = max(dp[j],dp[j-w[i]]+v[i])
print(dp[V])
多重背包Ⅰ
w表示重量 v表示价值
错误做法:
由于受到完全背包问题影响
我的思路:
顺着我认为多重背包1和完全背包的区别在于物品数量是有限的 那么要做的就是需要记录一下当前背包容量下物品的数量
所以我创建了一个二维数组s[ i ][ j ] i表示当前背包容量 j表示物品编号 在i背包容量情况下第j个物品的数量
那么顺着完全背包的思想 在当前背包容量下 当我们考虑完最后一个物品时就是当前最优解 那么我们在此时更新当前物品数量 在每次考虑能否放入物品时多添加一个判断-当前考虑物品数量是否为0
但是!
这有一个漏洞
当有
w:1 v:2
w:2 v:4
当前背包容量为2的情况下
我们没办法判断是拿两个w:1 v:2好 还是拿一个w:2 v:4好 因为此时的选取会影响后续的选取 由于当前无法判断是否为最优解 所以导致后续的判断也无法判断 所以这个做法是错误的
#define X 100
int v[X], w[X], s[X][X];//s为当前背包容量下最优解时每个物品数量
int main()
{
int N, V;
scanf_s("%d %d", &N, &V);
int v[X], w[X], s[X][X];//s为当前背包容量下最优解时每个物品数量
vector<vector<int>> dp(V + 1, vector<int>(N+1));
for (int i = 1; i <= N; i++)
{
scanf_s("%d %d %d", &w[i], &v[i], &s[0][i]);
}
for (int i = 1; i <= V; i++)
{
int temp[X] = { 0 };//临时存储当前情况下物品数量
for (int j = 1; j <= N; j++)
{
if (i - w[j] >= 0)
{
if (dp[i - w[j]][N] + v[j] >= dp[i][j - 1] && s[i - w[j]][j] != 0)//如果放入该物品价值更高 且该物品数量还有 那么久放入
{
dp[i][j] = dp[i - w[j]][N] + v[j];
memcpy(temp, s[i - w[j]], sizeof(s[i - w[j]]));//获取i-w[j]当前重量-想要放入物品重量情况时的最优物品数量
temp[j] = temp[j] - 1;//对该物品数量进行取出
}
else
{
dp[i][j] = dp[i][j - 1];
}
}
else
{
dp[i][j] = dp[i][j - 1];
}
}
memcpy(s[i], temp, sizeof(temp));//此时是对最后一个编号物品判定结束 那么此时的物品数量就是当前背包容量下的最优数量
}
for (int i = 0; i <= V; i++)
{
for (int j = 0; j <= N; j++)
{
printf("%d ", dp[i][j]);
}
cout << " ";
for (int k = 1; k <= N; k++)
{
printf("%d ", s[i][k]);
}
cout << endl;
}
printf("%d", dp[V][N]);
return 0;
}
正确做法:
我们应该把这道题考虑为有数量的普通01背包问题
那么我们只需要在每一次判断物品时考虑装多个物品就行了
例如在装物品1的时候就尝试装0个 1个 2个。。。s个
#include<bits/stdc++.h>
using namespace std;
const int X = 110;
int main()
{
int N, V;
scanf("%d %d", &N, &V);
int v[X], w[X], s[X];
vector<vector<int>> dp(V + 1, vector<int>(N+1));
for (int i = 1; i <= N; i++)
{
scanf("%d %d %d", &w[i], &v[i], &s[i]);
}
for (int i = 1; i <= V; i++)
{
for (int j = 1; j <= N; j++)
{
for(int k = 0;k<=s[j];k++)//多一个循环 在物品数量允许的情况下不断的添加物品 k为0的原因在于 要和dp[i][j-1]进行比较的同时 还要在不停的添加物品同时对数据进行更新
{
if (i -k * w[j] >= 0)
{
dp[i][j] = max(dp[i - k * w[j]][j-1] + k * v[j],dp[i][j]);
}
}
}
}
printf("%d", dp[V][N]);
return 0;
}
完全背包问题Ⅱ
区别在于这次每个物品的数量0-2000三重循环就会超时
那么这个优化的核心就在于
问题1是将一个物品分为了s个物品 然后对每个物品都尝试放入背包
例如先装0个 1个 2个。。。s个
那么我们为了优化 我们首先要知道
一个数字可以被分解成二进制 例如7(10) ->111(2)这样我们可以用
100 010 001表示7以内的所有数
那么我们假设一个物品有7个 我们分为3堆 1个 2个 4个此时我们就把一个物品变为了三个物品 然后进行最简单的0-1背包步骤就行了
核心:将一种物品按二进制分为log2n堆 每一堆就是一种物品 然后重新进行0-1背包就行了
#include<iostream>
#include<vector>
#include<stdio.h>
using namespace std;
struct item
{
int w;
int v;
};
int main()
{
int N, V;
int f[1000][1000] = {0};
//vector<vector<item>> it;
vector<item> t;
t.push_back({ 0,0 });//方便从第一个物品开始取 用来存储衍生的新物品
//it.push_back(t);
scanf_s("%d %d", &N, &V);
for (int i = 0; i < N; i++)
{
int x, y, z;
scanf_s("%d %d %d", &x, &y, &z);
//vector<item> temp;
for (int j = 1; j<=z; j *= 2)//根据物品数量衍生出新的物品进行存储
{
z -= j;
t.push_back({ x* j, j* y });
}
if (z > 0)//对最后多出来的那部分也进行存储
{
t.push_back({z * x,z * y});
}
}
/*这里做一个01背包就行了*/
for (int k = 1; k <= V; k++)//递增背包容量
for (int i = 1; i < t.size(); i++)//遍历每个物品
{
if (k - t[i].w >= 0)
f[k][i] = max(f[k][i - 1], f[k - t[i].w][i - 1] + t[i].v);
else
f[k][i] = f[k][i-1];
}
cout << f[V][t.size()-1];
return 0;
}
但是这个方法有问题 因为int f[1000][1000] = {0};开的太大了 一定要降为一维的
改进方法就是降低为一维
for (int i = 1; i < t.size(); i++)//遍历每个物品
for (int k = V; k >= 0; k--)//递增背包容量 这个一定有顺序要求
{
if (k - t[i].w >= 0)
f[k] = max(f[k], f[k - t[i].w] + t[i].v);
else
f[k] = f[k];
}
cout << f[V];
二维费用背包
在0-1背包一维优化的基础上拓展到二维就行了
单纯多了一个判断条件
#include<stdio.h>
#include<iostream>
#include<vector>
using namespace std;
#define X 10000
int dp[101][101] = {0};
int main()
{
int N,V,M;
scanf("%d %d %d",&N,&V,&M);
int w[X],v[X],vo[X];
for(int i = 1;i<=N;i++)
scanf("%d %d %d",&vo[i],&w[i],&v[i]);
for(int i = 1;i<=N;i++)
{
for(int j = V;j>=vo[i];j--)//多判断一层体积
{
for(int k = M;k>=w[i];k--)
{
dp[j][k] = max(dp[j][k],dp[j-vo[i]][k-w[i]]+v[i]);
}
}
}
cout<<dp[V][M];
return 0;
}





















 3850
3850











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








