排序算法的笔算与代码冲突解释

reason

• 在做题的时候根据不同题意运算的流程也不同，即使使用代码可以运行，但是正式手算的过程也有误差，所以这篇文章找一下他们的difference

• 宝藏视频，动态展示很nice
  算法运算动态视频展示
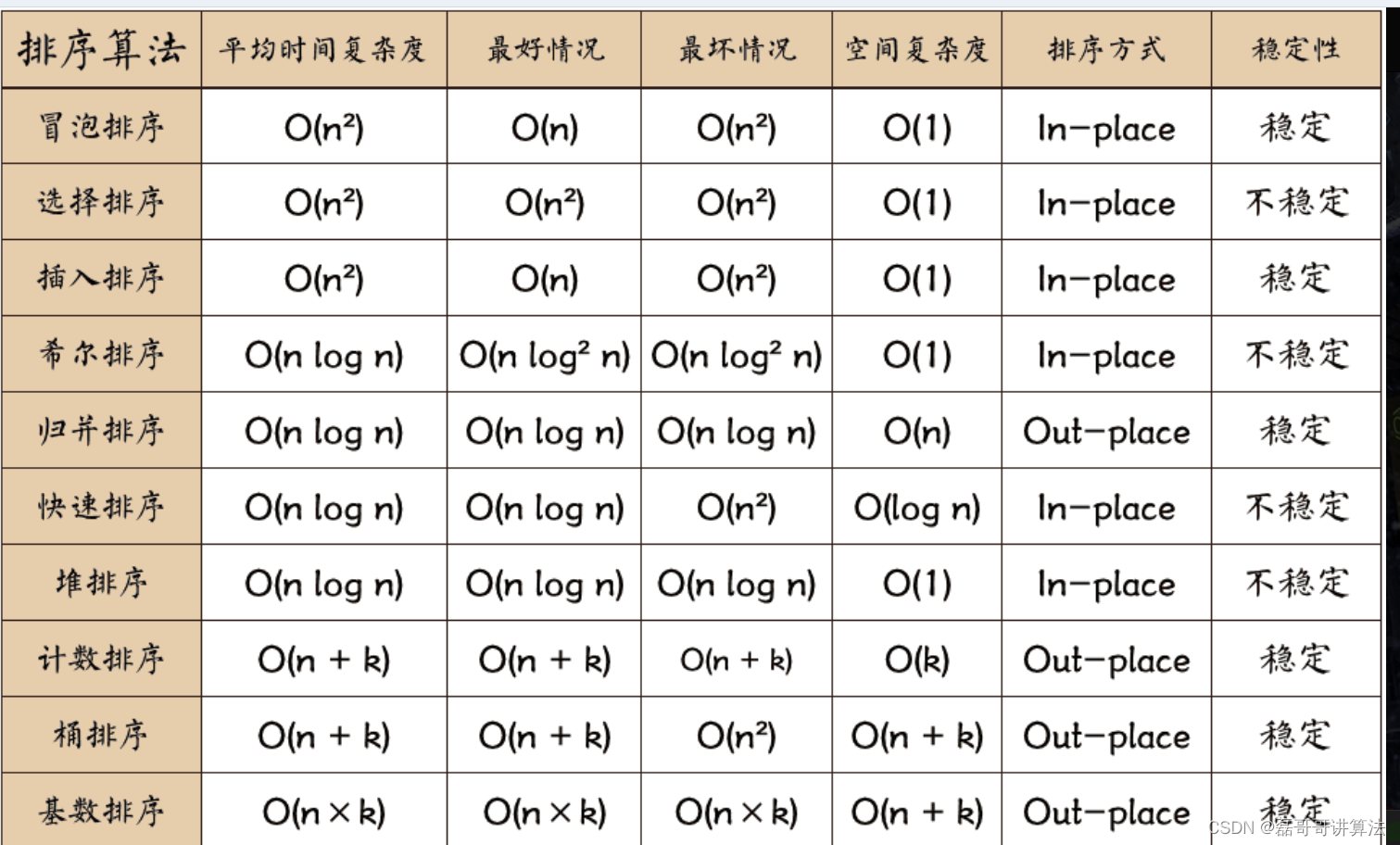
  常用算法信息表，注意一下希尔和快排，天大貌似很喜欢
  

• 数据元素：是数据（集合）的一个个体，它是数据的基本单位。

• 数据项：用来描述数据元素，数据的最小单位。

• 数据对象：具有相同性质的若干个数据元素的集合，如整数数据对象是所有整数的集合。

• 数据结构：是相互之间存在一种或多种特定关系的数据元素的集合。（集合中的数据元素可按照数据项分类，数据元素的集合有构成了数据对象）。

• 数据结构=数据对象+数据元素结构

• 数据结构的构成：逻辑结构（面向程序员的数据之间的结构）、存储结构（面像机器存储的实际物理结构）、数据运算（施加在该数据的运算）。

• 数据运算是对数据的操作，分为：运算描述和运算实现。

• 数据类型，是一个值的集合和定义在此集合上的一组操作的总称。

• 抽象数据类型=逻辑结构+抽象运算

• 抽象数据类型（（ADT））指的是从求解问题的数学模型中抽象出来的数据逻辑结构和运算（抽象运算）， 而不考虑计算机的具体实现 。

插入排序

插入排序其实是一个基础思维，在希尔排序中，我们可以理解为是设置了gap跳跃点+插入排序的手法实现，但实现的思路是分组gap排序比对。
提出此项，在此项前进行排序，每一个插入就是使得新的排序数组内存+1；

void insertsort(int a[],int n){
   for(int i=1;i<n;i++){
       int x=a[i],j=0;
       for(j=i-1;j>=0&&x<a[j];j--){
             a[j+1]=a[j];
       }
       a[j+1]=x;
   }
}

插入排序是拿首项往插入，如果有小就往前移动放置，不然就后放置，

希尔排序

希尔排序重点是选择gap也就是间距
从代码中可以看出来和插入排序是大相径庭的，但特点是gap的选择，也就是以gap大小为小组进行分组比较，如果有大小关系就可以进行交换，这就是一开始i设定是gap而不是像插入i=1，使得j=i-1的类推，希尔是j=i-gap，是j-=gap进行递推，重点是向右的排序移动。

void shellSort(int a[], int n){
    int gap=n/2;
    while(gap){
        for(int i=gap;i<n;i++){
            int x=a[i],j=0;
            for(j=i-gap;j>=0&&x<a[j];j-=gap){
                a[j+gap]=a[j];
            }
            a[j+gap]=x;
        }
        gap/=2;
    }
}

代码执行如此，那么手算的时候，我们就要根据gap进行划分数组比较，有涉及到大小关系的就可以交换

归并排序

首先根据理解是分而治之的思路，同时用代码实现的时候我们也是从中砍一半貌似与折半对比，但是归并排序是从小往上计算，我们的敲代码的实现逐渐变小交由计算机实现，那么手动计算的我们就要从核心往上算。
归并是2元组进对比，然后四元组，逐渐拼接成完整的对比数据链

void merge_sort(int l, int r)
{
    if (l >= r) return;
    int temp[N];
    int mid = l+r>>1;
    merge_sort(l, mid), merge_sort(mid+1, r);
    int k = 0, i = l, j = mid+1;
    while (i <= mid && j <= r)
    {
        if (a[i] < a[j]) temp[k ++ ] = a[i ++ ];
        else temp[k ++ ] = a[j ++ ];

    }
    while (i <= mid) temp[k ++ ] = a[i ++ ];
    while (j <= r) temp[k ++ ] = a[j ++ ];//前面是比较的排序
    for (int i = l, j = 0; i <= r; i ++ , j ++ ) a[i] = temp[j];
    //补回来新的排序之后的原数组 
}

从这段代码我们就可以发现手算模拟和代码思维实现的差别
为什么有额外数组temp[N]，也就是空间复杂上升为n的原因，存放每一组实现有序性数组，将排序后的temp再覆盖掉之前的a，主要是左侧开始拼凑嫁接，所以修改后的a是左侧。也就是为什么i要从L开始到区间R。

快速排序

最难理解，没有之一，也许是代码的高度凝练，大家也可以理解是左右侧移动标记点两向靠近，遇到重合点就将轴心数与相遇数进行交换。可是代码是如下实现的

#include<iostream>
#inlcude<bits/stdc++.h> //以后这个就是万能头文件，打比赛的时候用这个就行
const int N=1e5+10;
int q[N];
void quick_sort(int q[],int l,int r){
  int i=l-1,j=r+1;
  int x=q[(i+j)>>1];
  if(l>=r) return ;
  while(i<j){
  do i++ while (q[i]<x);
  do j-- while (x<q[j]);
  if(i<j) swap(q[i],q[j]);
  }
}
    quick_sort(q,l,j);
	quick_sort(q,j+1,r);
}
int main()
{
  int n;
  for(int i=0;i<n;i++)//因为最后的输出要的是一个拍好的数列，有没有说位置的时候，直接从简解决
   {
     scanf("%d",q[i]);
   }
   quick_sort(q,0,n-1);
}

在这个代码实现中，并不像天大笔试常见的选择中间，而是给定一个中轴值，对于中轴值使用流程在视频中流详细解释

黑线理解可以转换成
如果比较后动点<存储点的数，交换动点和存储点，然后存储点的位置+1继续进行新一轮的动点与存储点比较，当比较到结尾的时候，使得轴心点与最后的一个存储点交换，并且作为新的循环左右指数遍历运行，最后一个交换的存储指数就是新一轮的最有侧，轴心点也就是首轮的轴心点+1。
特许比较难理解，但确实是代码逻辑的实现过程
下面介绍另一种手算方式，思路来源是
手算快排速通
快速排序的原理是

• 选定基数
• 大于基数的放在右侧，小于的放在左侧（LR作为下标）
• 如果LR相遇则进行关于基数的对换然后继续重复12操作
  在执行的时候我们要注意如果轴值为数组首，那么从右侧R开始操作比如方便，如果有大小交换，那么就移动，并且将R的前进权交给L，如果不存在交换的情况，那么R就左移一格=下标减一，并将数字下拉。L也是如此，如果存在交换的情况，那么下标+1，直到LR相交的一点，将轴值放到LR上。
  例题
  
  比较高效的解决方案

小知识点

时间复杂度不会受到数据初始状态影响的而恒为nlog2n的是堆排序。
一趟排序结束后不一定能够选出一个元素放在其最终位置上的是希尔排序，不稳定，而且nlog2n与nlog2^2 n
霍夫曼有n个结点，叶子节点2m-1=n，空指针域为m+1

链表实现排序算法

选择排序

LinkList sortList(LinkList L) {
	LinkNode* p = L->next;
	LinkNode* q;
	LinkNode* min;
	int temp;
	while (p)
	{
		min = p;//有序序列中的最后位置元素节点
		q = p->next;
		while (q)
		{
			if (min->data > q->data)min=q;
			q = q->next;//寻找无序序列中的最小值节点
		}
 
		if (min!= p) {//交换data值
			temp = min->data;
			min->data = p->data;
			p->data = temp;
		}
		p = p->next;
	}
	return L;
}

冒泡排序

void BubbleSort(LinkList& L){
	LinkNode* q;
	if (p == NULL) //链表为空，比个毛线
	{
		return;
	}
	//求链表长度
	int length = Length(L);
	//每次排序都形成一个无序区中最大的元素，结束后长度减少1个。
	for (int i = 0; i < length; i++,length--){
		LinkNode* p = L->next;//每一趟开始都从第一个数据结点开始遍历
		while (p != NULL){
			q = p->next;
			if (q != NULL && p->data > q->data){
				swap(p->data, q->data);
			}
			p = p->next;
		}
	}
	
}

双向冒泡排序链表化

//基基于双向链表的双向冒泡排序法
#include <iostream>
#define MaxInt 32767 //（无穷大）
using namespace std;
typedef struct LNode{
	int data;
	LNode *next,*pre;
}LNode,*LinkList;
void Insert(LinkList &L,LinkList &rear){
	int data;
	cin>>data;
	rear->next=new LNode;
	rear->next->pre=rear;
	rear=rear->next;
	rear->data=data;
	rear->next=NULL;
	L->data++;
}
void Sort(LinkList &L,LinkList &rear){
	if(L==rear) return;//如果没有结点直接返回 
	LNode *h=L,*t=rear;//h表示每次正向遍历的起始位置的前一个指针，t表示每次反向遍历的尾指针 
	while(h->next!=t&&h!=t){
		LNode *p=h->next;
		while(p->next){//正向遍历 
			if(p->data>p->next->data){
				LNode *s=p->next;
				p->pre->next=s;
				if(s->next) s->next->pre=p;
				p->next=s->next;
				s->pre=p->pre;
				p->pre=s;
				s->next=p;
			}
			else p=p->next;
		}
		h=h->next;
		LNode *s=t;
		while(s->pre!=L){//反向遍历 
			if(s->data<s->pre->data){
				LNode *p=s->pre;
				p->pre->next=s;
				if(s->next) s->next->pre=p;
				p->next=s->next;
				s->pre=p->pre;
				p->pre=s;
				s->next=p;
			}
			else s=s->pre;
		}
		t=t->pre;
	}
}
int main(){
	int n;
	while(cin>>n&&n!=0){
		LinkList L,rear;//头结点、尾指针 
		L=new LNode;
		L->data=0;//存储链表长度 
		L->next=NULL;
		rear=L; 
		for(int i=1;i<=n;i++)//存入链表 
			Insert(L,rear);
		Sort(L,rear);//链表排序
		LNode *p=L->next;//输出链表 
		if(p){//输出第一个元素 
			cout<<p->data;
			p=p->next;
		}
		while(p){//输出后续元素 
			cout<<" "<<p->data;
			p=p->next;
		}
		cout<<endl;
	}	
	return 0;
} 

插入排序

void InsertSort(LinkList *head) {
	LinkList *p = head->next, *s, *t, *q = head;
	while (p) {
		t = head, s = head->next;
		//找到插入的位置
		while (s && s->data < p->data) {//p插入s之前
			t = s;
			s = s->next;
		}
		q->next = p->next;
		p->next = t->next;
		t->next = p;
		
		q = p;
		p = p->next;
	}
	
}

归并排序

/**
 * 返回中间节点
 * @param head
 * @return
 */
public ListNode split(ListNode head) {
    if (head == null) {
        return head;
    }

    ListNode prev = null;
    ListNode slow = head;
    ListNode fast = head;
  	// 注意这里了要判断fast.next 是否为空
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        prev = slow;
        slow = slow.next;
    }
    prev.next = null;   // 断开链表，返回后面一段的第一个节点

    return slow;
}

/**
 * 合并两个有序链表
 * @param left
 * @param right
 * @return
 */
public ListNode merge(ListNode left, ListNode right) {
    ListNode head = new ListNode(-1);
    ListNode cur = head;
    while (left != null && right != null) {
        if (left.val > right.val) {
            cur.next = right;
            right = right.next;
        } else {
            cur.next = left;
            left = left.next;
        }
        cur = cur.next;
    }

    while (left != null) {
        cur.next = left;
        cur = cur.next;
        left = left.next;
    }

    while (right != null) {
        cur.next = right;
        cur = cur.next;
        right = right.next;
    }


    return head.next;
}

public ListNode sortList(ListNode head) {
    if (head == null || head.next == null) {
        // 为空 或 只有一个链表节点均不用排序
        return head;
    }
    ListNode mid = split(head);
    ListNode left = sortList(head);
    ListNode right = sortList(mid);
    return merge(left, right);
}

非嵌套递归的归并排序

func MergeSort(list List) {
	// 如果链表没有元素或只有一个元素，那么不用排序
	if list.next == nil || list.next.next == nil {
		return
	}

	// 计算链表长度, 并找到分割点
	midNode := list
	shouldNext := true
	for i := list.next; i != nil; i = i.next {
		if shouldNext {
			midNode = midNode.next
		}
		shouldNext = !shouldNext
	}

	// 把链表分成两个子链表
	list1 := list
	list2 := &ListNode{next: midNode.next}
	midNode.next = nil

	// 分别对两个子链表递归处理
	MergeSort(list1)
	MergeSort(list2)

	// 归并且合并两个子链表
	list1 = list1.next
	list2 = list2.next
	tail := list
	tail.next = nil
	for list1 != nil && list2 != nil {
		if list1.data < list2.data {
			tail.next = list1
			list1 = list1.next
			tail = tail.next
		} else {
			tail.next = list2
			list2 = list2.next
			tail = tail.next
		}
	}

	for list1 != nil {
		tail.next = list1
		list1 = list1.next
		tail = tail.next
	}

	for list2 != nil {
		tail.next = list2
		list2 = list2.next
		tail = tail.next
	}
}

链式快排

struct node{
	node():next(NULL){}
	node(int d,node *n):data(d),next(n){}
	int data;
	node* next;
};
void swap(node *p,node *q){
	int temp=p->data;
	p->data=q->data;
	q->data=temp;
}
//tail is excluded in the sequence to be sorted
//actual parameter tail is NULL when first called
void quicksort(node *head,node *tail){
	if(head==NULL||head->next==tail||head==tail)
		return;
	node *p=head->next;
	node *p_small=head;
	int temp;
	while(p!=tail){
		if(p->data<head->data){
			p_small=p_small->next;
			if(p!=p_small)
				swap(p,p_small);
		}
		p=p->next;
	}
	if(p_small!=head){
		swap(p_small,head);
		quicksort(head,p_small);
	}
	quicksort(p_small->next,tail);
};


or
ListNode* partition(ListNode* head, ListNode* tail) {
	ListNode *p = head, *q = head;
	int pivot = head->val;
	while (q != tail) {
		if (q->val < pivot) {
			p = p->next;
			swap(p->val, q->val);
		}
		q = q->next;
	}
	swap(p->val, head->val);
	return p;
}

ListNode* quickSort(ListNode* head, ListNode* tail) {
	if (head == tail) return head;
	ListNode* mid = partition(head, tail);
	head = quickSort(head, mid);
	quickSort(mid->next, tail);
	return head;
}

ListNode* quickSortAll(ListNode* head) {
	if (!head || !head->next) return head;
	return quickSort(head, nullptr);
}

acwing链式快排

 ListNode* quickSortList(ListNode* head) {
        if(!head) return head;
        quickSort(head, NULL);
        return head;
    }

    void quickSort(ListNode* head, ListNode* tail)
    {
        if (head != tail)
        {
            int key = head->val;
            ListNode *p = head, *q = p->next;
            while(q != tail) {
                if(q->val < key) {
                    p = p->next;
                    swap(p->val, q->val);
                }
                q = q->next;
            }
            if(p != head)
                swap(head->val, p->val);

            quickSort(head, p);
            quickSort(p->next, tail);
        }
    }