图论算法汇总与差别详解

已于 2022-12-08 21:21:48 修改
阅读量306 收藏 1
点赞数 1
分类专栏： 进阶算法 算法 文章标签： 1024程序员节 图论 算法
于 2022-10-24 20:09:02 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_43621422/article/details/127499433
版权

前言

因为图论里算法比较复杂和乱，所以整理了一下，将其放在同一个程序里，比较执行。也是新的整理和理解。

white主调

  • topsort(拓扑) 出入度，degree的操作，同时要记录路径通常用queue q 系列存度，减完了就弹出
  • prim（最小生成树）通过点的外加dist[i] 与 g[i][j]的比较外加最小的点，邻接矩阵列表图
  • krustra算法（最小生成树）通过无向图中的引入的定理，找最短路径加入进去确定是不是连通图，用到寻根问祖里的find并查集，前提是自带比较的数据存储，所以添加了结构体里的operator 《运算符重载或者是struct cmp外加都可以。
    本文模拟板子用的两种数据格式
struct E {
	int a, b, w;
	bool operator<(const E& temp) {
		return this->w < temp.w;//重点是有序的
	}
}edge[N*2];
int find(int a) {
	if (p[a] != a)p[a] = find(p[a]);
	return p[a];
}

void add(int a, int b, int c) {
	e[idx] = b,w[idx]=c;
	ne[idx] = h[a];
	h[a] = idx++;
}
  • Dijkstra-朴素O(n^2)
    初始化距离数组, dist[1] = 0, dist[i] = inf;
    for n次循环 每次循环确定一个min加入S集合中，n次之后就得出所有的最短距离
    将不在S中dist_min的点->t
    t->S加入最短路集合
    用t更新到其他点的距离 dist[j]=min(dist[j],dist[u]+w[i]);
    新路径dist j 里是由之前的 dist u 加上新的连接上i 点的线构成
  • Dijkstra-堆优化O(mlogm)
    利用邻接表，优先队列
    在priority_queue[HTML_REMOVED], greater[HTML_REMOVED] > heap;中将返回堆顶
    利用堆顶来更新其他点，并加入堆中类似宽搜 queue q, q[++tt],都可以
  • Bellman_fordO(nm)
    注意连锁想象需要备份, struct Edge{inta,b,c} Edge[M];，也可以用hnewe四数组模拟
    初始化dist, 松弛dist[x.b] = min(dist[x.b], backup[x.a]+x.w);
    松弛k次，每次访问m条边
    *Floyd O(n^3)
    初始化d
    k, i, j 去更新d 松弛的祖师爷，它松弛程度比backup备份的bellman—ford更大，同时也很费时间，要是水题，可以用一下，共同点是 floyd和bell都用min放缩
  • Spfa O(n)~O(nm）
    这个算法很全面，既可以审闭环，也可以走负权值，比较全面。
    queue q 的队列存数据，先让所有能到达的点入队，然后遍历st变为true；每一次的使用就是弹出，然后算外延点的dist[j]=dist[u]+w[i]，还是u集合外加上 i 点边后的 dist[j]距离，同时把标记一下探索点，如果不在当前队列探索队里就加入，也许会出现之前加入过但是在遍历前被弹出，那也重新加入，这也就是解决闭环 负环 重换的情况优势。
if (dist[j] > dist[t] + w[i]) {
				dist[j] = dist[t] + w[i];  //更新距离
				cpa[j] = cpa[t] + 1;
				//如果大于等于n,则出现自己到自己的负环情况，则终止循环，表示存在负环
				if (cpa[j] >= n) return true;
				if (!st[j]) { //如果不在队列中
					q.push(j);
					st[j] = true;
				}
			}
  • 匈牙利算法
    理解为指派任务算法，在约束任务的前提下，获取最高的执行效率。以二分图为分支的图论
    匹配边所连接的点被称为匹配点。同样可以定义非匹配边和非匹配点。
    如果二分图里的某一个匹配包含的边的数量，在该二分图的所有匹配中最大，那么这个匹配称为最大匹配(Maximum Matching)有机会连接，没机会创造机会也要连接。
    ————————————————

代码集成实现

#include<bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
int dist[N], st[N], degree[N];
int h[N], ne[N], e[N], w[N],idx;
int n, m;//默认记点从0开始
int g[N][N],res;
void add(int a, int b, int c) {
	e[idx] = b,w[idx]=c;
	ne[idx] = h[a];
	h[a] = idx++;
}
void addtopsort(int a, int b) {
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}
//在topsort函数里
int q[N];
int hh = 0, tt = -1;
//模仿q和queue，存放好度数数据为0的就是已经遍历结束后入队列
void topsort() {
	for (int i = 0; i < n; i++) {
		if (degree[i] == 0) q[++tt] = i;
	}
	while (hh <= tt) {
		int a = q[hh++];
		for (int i = h[a]; i != -1; i = ne[i]) {
			int b = e[i];
			degree[b]--;
			if (degree[b] == 0)q[++tt] = b;
		}
	}//顺便记住了拓扑序列
	if (tt == n - 1)for (int i = 0; i < n; i++)cout << q[i] << " ";
	else cout << -1;//不是这一个线路里的
}
//如果变成了大量访问，那么就相当于是add构建一个基本图，然后query依次减，看看能不能依靠入度走完全程
/*for(int i=0;i<k;i++){
        for(int j=1;j<=n;j++){
            cin>>query[j];
            d[j]=degree[j];
        }
        if(topsort())demon[i]=1;
        else demon[i]=0;
    }
    for(int i=0;i<k;i++)
        if(!demon[i])
            cout<<i<<' ';
*/
//最短路径
void dijkstra(int u) {//朴素
	memset(dist, 0x3f, sizeof(dist));
	dist[u] = 0;
	for (int i = 0; i < n; i++) {
		int t = -1;
		for (int j = 1; j <=n; j++) {
			if (!st[t] && (t == -1 || dist[j] < dist[t]))t = j;
		}
		st[t] = true;
		for (int i = h[u]; i!= -1; i = ne[i]) {
			int j = e[i];
			dist[j] = min(dist[j], dist[t] + w[i]);
		}
	}
}
typedef pair<int, int> PII;
int heapdijkstra() {//堆优化之后迪杰特斯拉算法
	memset(dist, 0x3f, sizeof(dist));
	dist[1] = 0;
	priority_queue<PII, vector<PII>, greater<PII>>heap;//大跟堆first是值，second是序号
	//while(heap.size())都可以，反正还是要加入的
	heap.push({ 0,1 });
	while (!heap.empty()) {
		auto t = heap.top();
		heap.pop();
		int u = t.second, distance = t.first;
		if (st[u])continue;
		st[u] = true;
		for (int i = h[u]; i != -1; i = ne[i]) {
			int j = e[i];
			if (dist[j] > dist[u] + w[i]) {
				dist[j] = dist[u] + w[i];
				heap.push({ dist[j],j });
				/*不论是dijkstra里的什么
				理解是第 i的dist 是从1到u的距离加上外面的点i的距离变成新的dist i；
				最小值，可以使用min化
				dist[j]=min(dist[j],dist[u]+w[i])
				或者如果堆优化就要加入队列里新的dist路径，dist[j],j
				结合pII的数据结构设定，左侧距离，右侧点
				*/
			}
		}
	}
	if (dist[n] == 0x3f3f3f3f) return -1;
	return dist[n];
}
void prim()//考察的是点,同时在数据操作中也有变换，常面临的是邻接矩阵
{
	memset(dist, 0x3f3f, sizeof(dist));
	dist[0] = 0;
	for (int i = 0; i < n; i++) {
		int t = -1;
		for (int j = 0; j < n; j++) {
			if (!st[j] && (t == -1 || dist[j] < dist[t]))t = j;
		}
		st[t] = 1;
		res += dist[t];
		for (int i = 0; i < n; i++) {
			if (dist[i] > g[t][i] && !st[i])dist[i] = g[t][i];
		}
	}
	cout << res;
}
//krustra利用结构体
int p[N];
//并查集寻根问祖,也从侧面说明了针对的是边排序后加入最小判断=是否闭环
struct E {
	int a, b, w;
	bool operator<(const E& temp) {
		return this->w < temp.w;//重点是有序的
	}
}edge[N*2];
int find(int a) {
	if (p[a] != a)p[a] = find(p[a]);
	return p[a];
}
int cnt = 0;
void krustra() {
	for (int i = 0; i <= m; i++) {
		int pa = find(edge[i].a);
		int pb = find(edge[i].b);
		if (pa != pb) {
			res += edge[i].w;
			p[pa] = pb;
			cnt++;
		}
	}
}
bool isperfectpic(int cnt) {
	if (cnt < n - 1) {//如果保留的边小于点数-1，则不能连通
		cout << "impossible";
	}
}
int backup[N];//为了数组的稳定性
void bellman_ford() {
	memset(dist, 0x3f, sizeof(dist));
	dist[1] = 0;
	for (int i = 0; i < n; i++) {
		memcpy(backup, dist, sizeof dist);
		int flag = 0;
		for (int j = 0; j < m; j++) {
			int a = e[j], b = ne[a];//eg :边从a-b
			dist[b] = min(dist[b], backup[a] + w[a]);
		}
		/*Bellman - ford 算法是求含负权图的单源最短路径的一种算法，效率较低，代码难度较小。
		其原理为连续进行松弛，在每次松弛时把每条边都更新一下，若在 n - 1 次松弛后还能更新，
		则说明图中有负环，因此无法得出结果，否则就完成。找每一步的最短距离*/
	}
}
//松弛的祖师爷，矩阵列表g来确定dist.可以理解成dp
void floyd() {
	for (int k = 1; k <= n; k++) {
		for (int i = 1; i < n; i++) {
			for (int j = 1; j <= n; j++) {
				g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
			}
		}
	}
}
//可以用q数组存队列，也可以直接queue<int> q;
void spfa() {
	q[++tt] = 1;
	dist[1] = 0;
	st[1] = 1;//找起点，或者默认1也行
	while (hh <= tt) {
		int a = q[hh++];
		st[a] = false;
		for (int i = h[a]; i != -1; i = ne[i]) {
			int j = e[i];
			if (dist[j] > dist[a] + w[i]) {
				dist[j] = dist[a] + w[i];
				if (!st[j]) {
					q[++tt] = j;
					st[j] = 1;//spfa反复入队
				}
			}
		}
	}
}
int cpa[N];//计算环
int spfaque() {
	queue<int> q;
	for (int i = 1; i <= n; i++) {
		st[i] = true;
		q.push(i);
	}
	while (q.size()) {
		int t = q.front();
		q.pop();
		st[t] = false;
		for (int i = h[t]; i != -1; i = ne[i]) {
			int j = e[i];
			if (dist[j] > dist[t] + w[i]) {
				dist[j] = dist[t] + w[i];  //更新距离
				cpa[j] = cpa[t] + 1;
				//如果大于等于n,则出现自己到自己的负环情况，则终止循环，表示存在负环
				if (cpa[j] >= n) return true;
				if (!st[j]) { //如果不在队列中
					q.push(j);
					st[j] = true;
				}
			}
		}
	}
}
int main(){
	scanf("%d %d", &n, &m);
	memset(st, 0, sizeof(st));
	memset(h, -1, sizeof(h));
	memset(g, 0x3f, sizeof(g));
	for (int i = 0; i < m; i++) {
		int a, b, c;
		scanf("%d %d %d", &a, &b, &c);
		add(a, b, c);
		addtopsort(a, b);
		g[a][b] = c;
		degree[b]++;
		edge[i] = { a,b,c };//结构的加入
	}
	sort(edge + 1, edge + m + 1);
	krustra(); isperfectpic(cnt);//同样可以运用于topsort和最小生成单支树，也可以求res
	topsort();//是否是完整图
	prim();//求最小生成树，res，返回前序结点，周游的路径
	int u;//以某点为起点的遍历，更有应用实践性
	dijkstra(u);
	heapdijkstra();//多快好省
	bellman_ford();
	floyd();
	spfa();//spfaque同理，可以用queue看着更舒服
	//解决负权值的问题，性价比比较高，价值等同于堆优化的dij
	//可以理解成松弛的用min，其他的都比较一下好用于数据的其他操作
}

下面讲一道融合上面所以算法思路和代码的应用题，也许有点烧脑，但也是将知识点融合的好题
判断有无向图，有无正负权值，连通图，find并查集 dijkstra

航路与道路

农夫约翰正在一个新的销售区域对他的牛奶销售方案进行调查。他想把牛奶送到 T 个城镇，编号为 1∼T。
这些城镇之间通过 R 条道路 (编号为 1 到 R) 和 P 条航线 (编号为 1 到 P) 连接。
每条道路 i 或者航线 i 连接城镇 Ai 到 Bi，花费为 Ci。
对于道路，0≤Ci≤10,000;然而航线的花费很神奇，花费 Ci 可能是负数(−10,000≤Ci≤10,000)。
道路是双向的，可以从 Ai 到 Bi，也可以从 Bi 到 Ai，花费都是 Ci。
然而航线与之不同，只可以从 Ai 到 Bi。
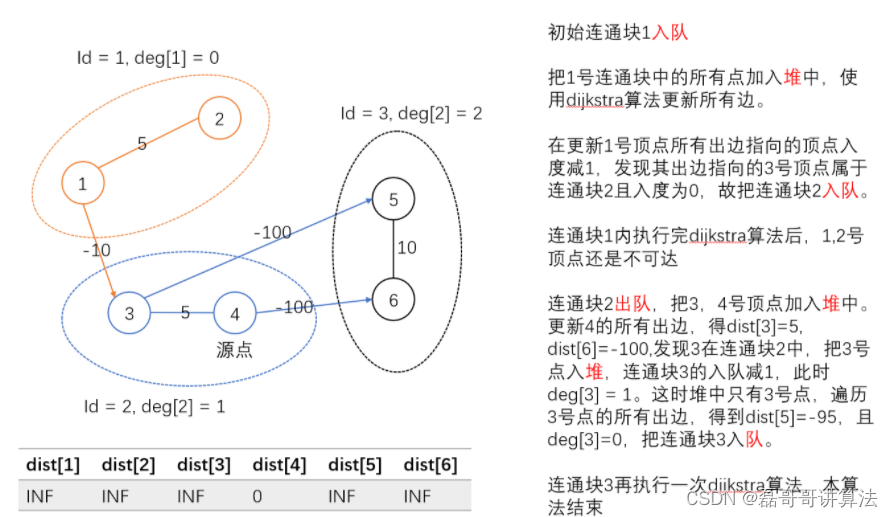
事实上，由于最近恐怖主义太嚣张，为了社会和谐，出台了一些政策：保证如果有一条航线可以从 Ai 到 Bi，那么保证不可能通过一些道路和航线从 Bi 回到 Ai。
由于约翰的奶牛世界公认十分给力，他需要运送奶牛到每一个城镇。
他想找到从发送中心城镇 S 把奶牛送到每个城镇的最便宜的方案。
在这里插入图片描述
下图重点解释，如何将道路和航路的两种复合图连通在一起，并进spfa（）算法可以算的同时
也可以用通过topsort 并查集 dijkstra实现的方法，第二种方法更好理解，也是主流思想，不会拘束与数据问题
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int dist[N];
typedef pair<int,int> PII;
bool st[N];
int n,mr,mh,s,e[N],h[N],ne[N],idx,w[N];
int id[N],deg[N],bcnt;
int q[N],hh,tt=-1;
vector<int> block[N];
void add(int a,int b,int c){
    e[idx]=b,w[idx]=c;
    ne[idx]=h[a];
    h[a]=idx++;
}
void dijkstra(int block_id){
    priority_queue<PII,vector<PII>,greater<PII>>heap;
    for(int u:block[block_id]){
        heap.push({dist[u],u});
    }
    while(heap.size()){
        PII t=heap.top();
        heap.pop();
        int u=t.second;
        if(st[u])continue;
        st[u]=true;
        for(int i=h[u];i!=-1;i=ne[i]){
            int j=e[i];
            if(dist[j]>dist[u]+w[i]){
                dist[j]=dist[u]+w[i];
                if(id[j]==block_id)heap.push({dist[j],j});
            }
            if(id[j]!=block_id&&--deg[id[j]]==0)q[++tt]=id[j];
        }
    }
}
void dfs(int u){
    lock[bcnt].push_back(u);
    id[u]=bcnt;
    for(int i=h[u];i!=-1;i=ne[i]){
        int j=e[i];
        if(!id[j])dfs(j);
    }//找链接
}
void topsort(){
    memset(dist,0x3f,sizeof(dist));
    dist[s]=0;
    for(int i=1;i<=bcnt;i++){
        if(!deg[i])q[++tt]=i;
    }
    while(hh<=tt){
        int t=q[hh++];
        dijkstra(t);
    }
}


int main(){
    memset(h,-1,sizeof(h));
    scanf("%d %d %d %d",&n,&mr,&mh,&s);
    for(int i=0;i<mr;i++){
        int a,b,c;
        scanf("%d %d %d",&a,&b,&c);
        add(a,b,c),add(b,a,c);
    }
    for(int i=1;i<=n;i++){
        if(!id[i]){
            ++bcnt;
            dfs(i);
        }
    }
    for(int i=0;i<mh;i++){
        int a,b,c;
        scanf("%d %d %d",&a,&b,&c);
        add(a,b,c),deg[id[b]]++;
    }
    topsort();
    for(int i = 1; i <= n; i++)
    {
        if(dist[i] > 0x3f3f3f3f / 2) puts("NO PATH");
        else printf("%d\n", dist[i]);
    }
    return 0;
}

AOE图与AOV图

工序代号是弧线，事件是点集合

事件是v点

  • 在一个有向图中，顶点表示事件，有向边表示活动，边上的权值表示活动的持续时间。
  • 关键路径：活动的持续时间又称为路径长度，把源点到终点的具有最大长度的路径叫为关键路径。
  • 关键路径又可以理解为同一个层次的事件，所占用的最大时间，那么关键路径必然经过这个事件。
  • 活动的最晚开始时间和最晚开始时间相等，那么该活动就是关键活动，活动的路径就是关键路径
    前提是拓扑排序是正序，逆序拓扑顺序是倒着来，执行是安排的倒着往前推。
    etv：事件最早发生时间max正拓扑
    ltv：事件最晚发生时间，etv和ltv 的时间安排是首尾一致min逆拓扑
    ete：活动最早开始时间弧尾max
    lte：活动最晚开始时间，时间-线权

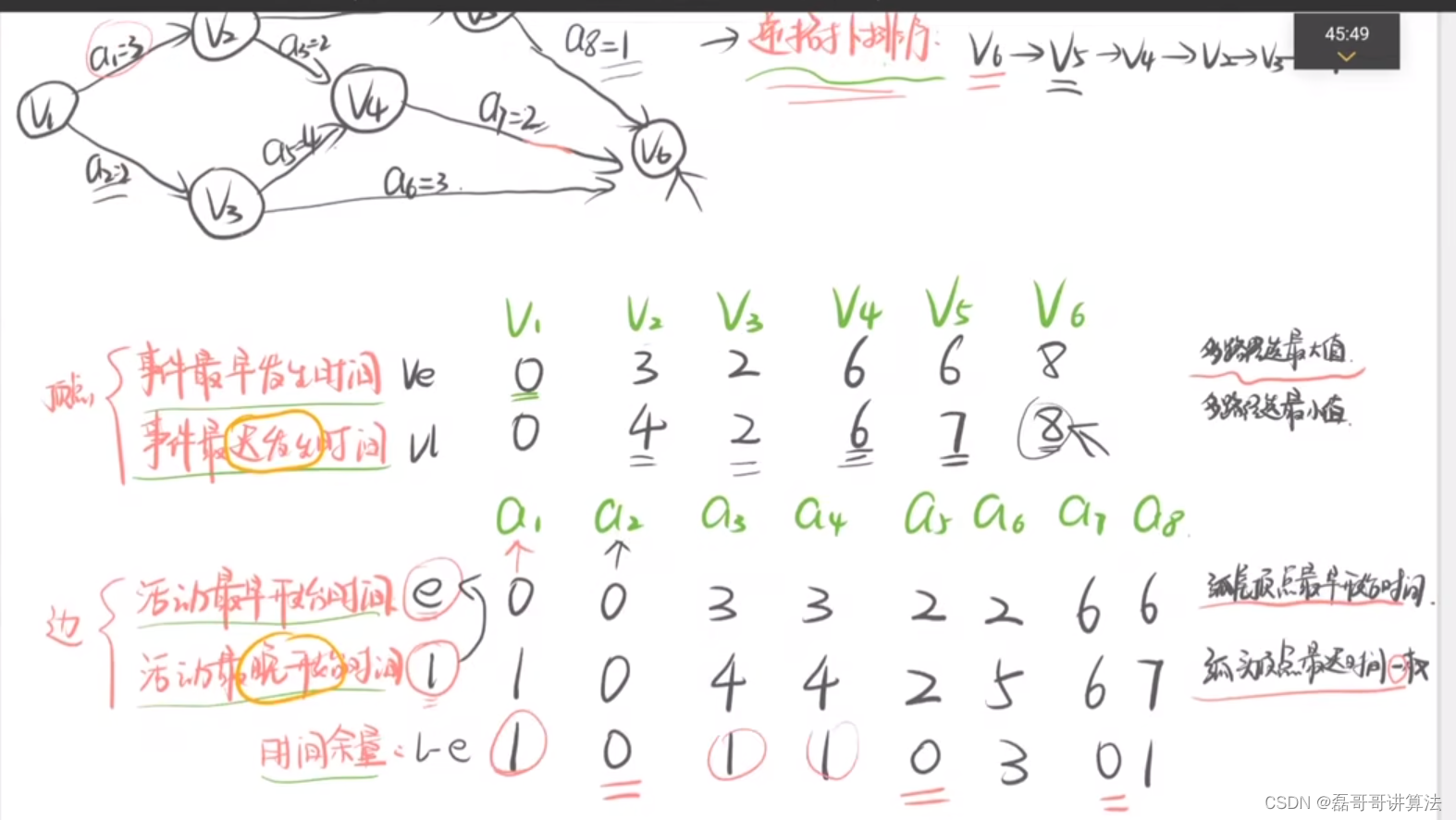
请添加图片描述

  • 是求该事件最早发生的时间，实际上就是求之前路径的最大权值之和。因为只有所有事件都发生了，下面一个事件才能开始发生，也就是事件的最早开始时间

  • ltv是求事件最晚发生时间，就是只要那个大事件还未结束，它在它本身的边权值上时间之前发生即可，是倒着推时间减去对应的边权值

活动是弧线

关键活动是按照时间余量作差后相等就是关键事件

  • 活动的最晚发生时间lte：就是在该事件最晚发生，减去该边的持续时间，就是事件最迟时间按照拓扑排序的顺序减去连接弧线的时间。操作的是弧首。

  • 活动最早发生时间：就是该事件最早发生时。也就是正序拓扑的弧尾结点所需要的时间

  • 当活动最早发生时间和活动最晚发生时间相等时，该活动所在的弧就是关键路径。

  • 当活动最早发生时间和活动最晚发生时间相等时，该活动所在的弧就是关键路径。

#include<iostream>
using namespace std;
#define MAX 25

typedef char Vertype;
typedef int Edgetype;
typedef int Status;

//构造图的有向图的邻接表结构体
typedef struct EdgeNode//边表结点  存放每个顶点的邻接点
{
	int adjvex;//边表下标
	Edgetype weight;//边表权重  若边不存在时即无NULL
	struct EdgeNode* next;//指向下一个邻接点
}EdgeNode;

typedef struct VerNode//顶点表   存放顶点
{
	int in;
	Vertype data;//顶点元素
	EdgeNode* firstedge;
}VerNode, AdjList[MAX];//邻接表的 顶点元素 和指向邻点的指针

typedef struct
{
	AdjList adjList;//邻接表
	int numVer, numEdge;//顶点数目和边的数目
}GraphAdjList;

//构造两个栈
typedef struct Stack
{
	int data[MAX];
	//int pop;
}SqStack;

//生成邻接表
Status CreatGraph(GraphAdjList& G)
{
	int i, j, k;
	Edgetype w;
	EdgeNode* e;
	cout << "Enter the number of vertices :" << endl;
	cin >> G.numVer;
	cout << "Enter the number of Edges :" << endl;
	cin >> G.numEdge;

	cout << "Input vertex content :" << endl;
	for (i = 0; i < G.numVer; i++)
	{
		cin >> G.adjList[i].data;//输入顶点元素
		G.adjList[i].in = 0;
		G.adjList[i].firstedge = NULL;//初始化邻边表为NULL；
	}

	for (k = 0; k < G.numEdge; k++)
	{
		cout << "Enter the vertex number of the edge (Vi->Vj)" << endl;
		cin >> i;
		cin >> j;

		cout << "Enter the weight of edge" << i << "-" << j << endl;
		cin >> w;
		e = new EdgeNode;//将两个顶点相结即可。
		e->adjvex = j;// 邻接序号为j
		e->next = G.adjList[i].firstedge;//i的第一个邻接指针 为e的指针
		e->weight = w;
		G.adjList[i].firstedge = e;
		G.adjList[j].in++;

		//有向图则只有生成一次即可
		/*
		e = new EdgeNode;
		e->adjvex = i;//无向图 重复一遍
		e->next = G.adjList[j].firstedge;
		G.adjList[j].firstedge = e;
		e->weight = w;*/
	}
	return 0;
}


SqStack* etv, * stack2;
SqStack* ltv;/*事件最晚发生时间*/
int top2;
//拓扑排序
Status TOpologicalSort(GraphAdjList& G)
{
	EdgeNode* e;
	//SqStack Q;
	int i, j, k, gettop;
	int top = 0;
	int count = 0;

	SqStack* Q;
	Q = new SqStack;
	for (i = 0; i < G.numVer; i++)
	{
		if (G.adjList[i].in == 0)
			Q->data[++top] = i;//存放入度为0的顶点
	}

	top2 = 0;/*初始化 事件最早发生的时间为0*/
	//SqStack *etv,*stack2;
	etv = new SqStack;
	for (i = 0; i < G.numVer; i++)
	{
		etv->data[i] = 0;
	}

	stack2 = new SqStack;
	while (top != 0)
	{
		gettop = Q->data[top--];//弹出入度为0的下标
		stack2->data[++top2] = gettop;//按照拓扑顺序保存弹出顶点下标
		count++;//统计拓扑网顶点数目

		//后面输出其边顶点
		//并删除边，使得边顶点入度-1
		for (e = G.adjList[gettop].firstedge; e; e = e->next)
		{
			j = e->adjvex;
			if (!(--G.adjList[j].in))//如果入度为1时  自减后进入循环   如果入度不为1，自减后 相当于边的数目减1
			{
				Q->data[++top] = j;//保存后续入度为0的顶点
			}

			/**/
			if ((etv->data[gettop] + e->weight) > etv->data[j])
			{
				etv->data[j] = etv->data[gettop] + e->weight;//保存权值   etv初始化都为0，
			}
		}
	}
	if (count < G.numVer)
	{
		cout << "不是一个网图" << endl;
		return 1;
	}
	else
	{
		cout << "是一个网图" << endl;
		return 0;
	}
	//return 0;

}

Status CriticalPath(GraphAdjList& G)
{
	EdgeNode* e;
	int i, j, k, gettop;
	int ete, lte;/*活动最早发生时间ele  活动最迟发生时间lte*/


	ltv = new SqStack;
	/*初始化ltv*/
	for (i = 0; i < G.numVer; i++)
	{
		ltv->data[i] = etv->data[G.numVer - 1];
	}
	while (top2 != 0)
	{
		gettop = stack2->data[top2--];
		for (e = G.adjList[gettop].firstedge; e; e = e->next)
		{
			k = e->adjvex;
			if (ltv->data[k] - e->weight < ltv->data[gettop])
			{
				ltv->data[gettop] = ltv->data[k] - e->weight;
			}
		}
	}
	for (j = 0; j < G.numVer; j++)
	{
		for (e = G.adjList[j].firstedge; e; e = e->next)
		{
			k = e->adjvex;
			ete = etv->data[j];
			lte = ltv->data[k] - e->weight;
			if (ete == lte)
			{
				cout << G.adjList[j].data << G.adjList[k].data << e->weight << endl;
			}
		}
	}
	return 0;
}

int main()
{
	GraphAdjList G;
	CreatGraph(G);
	TOpologicalSort(G);
	CriticalPath(G);
	system("pause");
	return 0;
}
磊哥哥讲算法
关注
  • 1
    点赞
  • 踩
  • 1
    收藏
    觉得还不错? 一键收藏
  • 打赏
    打赏
  • 0
    评论
专栏目录
图像差异对比算法_图像差异
cunbei2644的博客
09-28 5273
图像差异对比算法Was having fun today with idiff.php - a PHP shell script to tell you if two images are visually different by comparing them pixel by pixel. If there's a difference, the script creates a third ...
图论相关算法汇总（一）
陈 浩
09-15 3523
一、图的存储结构       这里，着重讲利用邻接表的存储，邻接表的处理方法是这样的：     （1）图中顶点用一个一维数组存储，当然，顶点也可以用单链表来存储，不过，数组可以较容易的读取顶点的信息，更加方便。     （2）图中每个顶点vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以，用单链表存储，无向图称为顶点vi的边表，有向图则称为顶点vi作为弧尾的出边表。具体如下图所示
模糊综合评价
weixin_53401658的博客
07-04 5775
模糊性常常是信息浓缩所致，目的是为了提高交换的概率，所以不是毫无用处，而是积极的特性。模糊是指客观事物差异的中间过渡中的“不分明性”或“亦此亦彼性”。​​​​​​​模糊数学是用来处理涉及模糊概念的问题，尝试使用某种方法将模糊的概念量化，方便进行处理计算。​​​​​​​模糊综合评价是模糊数学在评价类问题的一大应用，也就是处理涉及模糊概念的评价类问题。.........
leetcode(图论专题)
qq_46517733的博客
12-17 1673
图论1.导论2.编程题2.1 127. 单词接龙 1.导论 2.编程题 2.1 127. 单词接龙 字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列： 序列中第一个单词是 beginWord 。 序列中最后一个单词是 endWord 。 每次转换只能改变一个字母。 转换过程中的中间单词必须是字典 wordList 中的单词。 给你两个单词 beginWord 和 endWord 和一个字典 wordList ，找到从 beginWord 到
NOI图论算法：网络流
青少年趣味编程
02-19 214
网络流 https://www.bilibili.com/video/BV15p4y1C7zW https://www.bilibili.com/video/BV1HE411Y7sM https://www.bilibili.com/video/BV1rW411K7A9 https://www.bilibili.com/video/BV1Jt4y1U79c https://www.bilibili.com/video/BV1Da4y1t7bi https://www.bilibili.com/v
【算法】—贪心算法详解
DAY I 的成长之路
04-02 7474
！翻硬币快乐司机旅行家的预算买卖股票的最好时机I买卖股票的最好时机IIPrim算法_CSDN博客_prim算法dijstra求最短路径最小花费。
数学建模算法学习——各类模型算法汇总
热门推荐
qq_43042024的博客
09-08 2万+
相关模型解决的问题 数据分析类算法一览 100个经典动态规划方程 优化问题 线性规划 简介：线性规划的目标函数可以是求最大值，也可以是求最小值，约束条件的不等号可以是小于号也可以是大于号。为了避免这种形式多样性带来的不便，Matlab 中规定线性规划的标准形式为 其中 c 和 x 为 n 维列向量， A 、 Aeq 为适当维数的矩阵， b 、 beq 为适当维数的列向量。 代码实现 ...
AI算法初识之分类汇总
初心不忘产学研的博客
02-15 2518
AI算法的分类方式多种多样，可以根据不同的学习机制、功能用途以及模型结构进行划分。- 线性回归（Linear Regression）- 逻辑回归（Logistic Regression）- 决策树（Decision Tree）- 随机森林（Random Forest）- 支持向量机（Support Vector Machines, SVM）
图论算法软件图论算法软件
06-02
图论算法软件图论算法软件
图论算法软件Graph.exe
02-03
Graph.exe是一个图论算法软件，用于执行各种图论算法。它可以用来解决图论问题，如最短路径、最小生成树、网络流等。用户可以输入图的结构和权重，然后选择所需的算法进行计算，最后得到相应的结果。该软件可以帮助...
MATLAB算法图论算法软件
最新发布
04-15
MATLAB算法图论算法软件提取方式是百度网盘分享地址
MATLAB算法图论算法代码
04-15
MATLAB算法图论算法代码提取方式是百度网盘分享地址
Python 图论算法实现工具——NetworkX1
08-03
1.前言前段时间和几位小伙伴一起学习数学建模，其中解决拼接碎纸片问题（2013年全国大学生数学建模B题1）时候使用了图的模型，虽然Matlab解决具体的图论问题
电子科技大学《高级算法设计与分析》问题汇总
青年有志
12-18 1160
对于背包问题，当所有输入数值（包括背包的大小和各个物品的价值和体积）都是长整型（即整数）时，动态规划算法确实可以在多项式时间内求解。让我们更详细地分析这个问题。背包问题的动态规划算法的时间复杂度是 (O(nW))，其中 (n) 是物品的数量，而 (W) 是背包的容量。这意味着算法的时间复杂度取决于背包容量 (W) 的数值大小和物品数量 (n)。如果 (W) 和 (n) 都是整数，并且在合理的范围内，那么这个问题可以在多项式时间内求解。重要的是要注意，多项式时间是针对输入大小（即输入数据的比特数）而言的。
c++最全进制转化（含算法和函数分析）
磊哥哥讲算法
09-07 5463
数制：计数的方法，指用一组固定的符号和统一的规则来表示数值的方法数位：指数字符号在一个数中所处的位置基数：指在某种进位计数制中，数位上所能使用的数字符号的个数位权：指在某种进位计数制中，数位所代表的大小，即处在某一位上的“1”所表示的数值的大小。这些东西等一会涉及到二进制的核心思想，从某种程度上讲，其他转二位作为一个环节跳板，然后转到目的进制。
入门基础算法经典模板题
磊哥哥讲算法
03-31 940
引言 从acwing和pta中经典的数据结构与算法习题汇总，对于比较精髓的一些题，会重点详解，力求代码的优美和逻辑讲述的清晰。 快速排序 输入共两行，第一行包含整数 n。 第二行包含 n 个整数（所有整数均在 1∼109 范围内），表示整个数列。 #include<iostream> #inlcude<bits/stdc++.h> //以后这个就是万能头文件，打比赛的时候用这个就行 const int N=1e5+10; int q[N]; void quick_sort(int
动态规划DP模板题汇总
磊哥哥讲算法
07-04 797
动态规划模板题，详细分析了思路和基础模板，也将每种类型的DP以题目和题解分开讲述，以加深理解
图论算法及matlab算法实现
10-08
图论算法是一种在图结构中进行问题求解的算法。图结构是由节点和边组成的集合，通常用于表示各种实际问题，如社交网络、物流网络等。图论算法旨在解决与图相关的问题，如最短路径、最小生成树、最大流等。 图论算法包括许多不同的方法和技术，如深度优先搜索（DFS）、广度优先搜索（BFS）、迪杰斯特拉算法、克鲁斯卡尔算法、Prim算法等。这些算法根据不同的问题需求，采用不同的策略来搜索和遍历图结构，以达到解决问题的目的。 Matlab是一种数学软件，也可以用来实现图论算法。Matlab提供了丰富的函数和工具箱，可以方便地处理图结构和实现各种图论算法。Matlab中可以使用矩阵来表示图的节点和边，然后利用相关函数和工具箱进行图的遍历、搜索和计算。 例如，通过Matlab可以使用DFS或BFS算法来遍历图中的节点，找到特定节点之间的路径。可以使用迪杰斯特拉算法来计算图中两个节点之间的最短路径，或者使用克鲁斯卡尔算法或Prim算法来计算图的最小生成树。Matlab还提供了可视化功能，可以将图结构和算法结果以图形方式显示出来。 总的来说，图论算法是解决图相关问题的一种方法，而Matlab是一种可用于实现和计算图论算法的工具。通过结合图论算法和Matlab的功能，可以快速有效地解决各种与图相关的问题。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

磊哥哥讲算法

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值