论文笔记---SSH

在这里，我们设计了一个与SSH模型完全相似的一维周期声学系统。声学系统的单元由两个谐振腔和连接它们的两个连接管组成。我们表明，当我们调整控制细胞间和细胞内跳的连接管的半径时，我们的声学模拟发生拓扑相变。拓扑相变的特征是几何Zak相位的突变。

在三维系统中，两个带在Weyl点处线性相交，一个Weyl点是Berry通量的源或流，即以其Berry曲率的表面积分为特征的拓扑电荷。在二维(2D)系统中，Berry曲率的表面积分用Chern数表示。此外，对于一维系统，Berry连接的积分被定义为Zak相位。

在一维系统中，具有拓扑非平凡相的最具代表性的模型之一是Su-SchriefferHeeger (SSH)模型。该模型描述了电子在单细胞节理处的交错跳，该模型将电子的跳分为胞内跳和胞间跳两种。通过控制振幅，一维链的能带间隙可以闭合和重新打开，这意味着拓扑相变。

---

在一维系统中，如果胞间跳强大于胞内跳强，则该系统具有拓扑非平凡相。如果胞内跳强度大于胞间跳强度，则系统具有拓扑平凡相。

间>内  非平凡

间<内   平凡

当两个拓扑相不同的晶格连接时，会出现拓扑界面态。拓扑边缘态可以由单个拓扑非平凡声子晶体实现。

---

声子晶体由圆柱形波导和周期性交替结构的谐振腔组成

每个单元由两个相同的垂直方向的圆柱形腔作为谐振腔和两个水平方向的不同半径的圆柱形管作为连接点组成

图1所示。(a)实验装置。实验系统由一个扬声器和四个麦克风组成。该样品是由两种声子晶体组成的声波导。这些声子晶体是相互连接的，连接处用洋红色的箭头标出。声子晶体在结的每一边都有一个单位单元a或单位单元b，每一边的单位单元分别用红色和绿色虚线框标出。声波由扬声器产生，并沿波矢量k(由蓝色箭头表示)的方向在声学系统中传播。(b)和(c)分别标注a单元和b单元的截面及其几何参数。

每种声子晶体都类似于SSH模型，垂直(水平)圆柱腔对应于位点(键)。

a单元的草图如图1(b)所示，尺寸为a=200mm, t=5mm, r=40mm, h=80mm, w1=13mm, w2=20mm。 b单元示意图如图1(c)所示，其几何参数与a单元相同，除了w1=20 mm, w2=13 mm。

如图所示，单元胞中心半径为w2的导波结管控制胞间跳变，单元胞内跳变由单元胞边界附近半径为w1的导波结管控制。系统中充满空气，且样品的壁厚t足够大(>2 mm)，可以视为刚性边界。在模拟过程中，在每个单元单元的周期面上使用BlochFloquet边界条件，在其他边界上应用健全的硬边界条件。

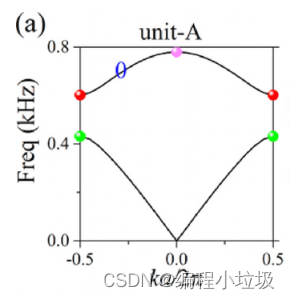
单元A B的能带图如图2(a),(c)所示：

C单元的能带结构在图2(b)，参数w1=w2=16.5（内外一样大）

边界带状态的本证模 a--d  c--e

 从图2(d)和图2(e)可以看出，本征模的声场压力沿波传播方向(x方向)变化，在z方向几乎一致。

所有的特征模对于反演中心都是对称或反对称的。每个波段的Zak相位可以由这些特征模的对称性来确定。

例如，在图2(a)，第二带下沿和上沿的特征模对称性相同，因此，Zak相位为0。同样，在图2(c)中，第二带下沿和上沿的特征模对称性不同，因此，Zak相位为p。

---

每个波段的Zak相位可以定义为

其中k是布洛赫准动量，为周期布洛赫函数，为布洛赫波，a为周期。

更具体地说，我们的声学系统的第n个隔离带的Zak相位可以表示为

 其中，hnZak代表第n波段的Zak相位，ρ是空气密度，v为空气中的声速，un,k(x, y, z)为带波向量k的第n波段状态归一化Bloch本征函数的胞内周期性部分。

如果所选单元格具有镜像对称性，则Zak相位的值要么等于0，要么等于p。

---

本文研究的声子晶体的拓扑特性可以通过各个单元的几何参数来调制。

改变两个水平连接管的半径差来实现拓扑相变

黑线和红线分别表示对称和反对称带边模式。很明显，随着dw的增大，频带闭合再打开，临界点dw=0（w1=w2）是频带反转点。

每个带隙的拓扑相位可以由带隙以下所有体带的Zak相位的总和来确定。

第1带隙的拓扑相用蓝色(Zak相0)和红色(Zak相p)标记。上下带边缘的对称分布是由于我们的系统在布里渊区边界附近的手性对称。

通过在一定的带隙内连接两个拓扑相位不同的声子晶体，可以实现拓扑界面。

在图1(a)中，选择左侧声子晶体的半径差为dw= -7 mm，选择右侧声子晶体的半径差为dw=7 mm(整个结构称为S1)。S1的特征模如图4(d)所示

为了便于比较，dw的另一组值分别在左右两侧为dw=-7 mm和dw=- 3mm(整个结构称为S2)。S2的本征模如图4(a)所示，可以观察到在带隙中间(红线表示)存在具有本征频率的本征模。

 

这一对比证明了拓扑相变发生时出现拓扑界面态，这意味着在结两侧的两个声子晶体的拓扑相是不同的。

S1对应透射光谱的结果如图4(e)和图4(f)所示。

此外，对S2的透射光谱进行了模拟和测量，结果分别如图4(b)和图4(c)所示。

对比S1和S2的透射光谱，无论是模拟的还是实测的S1透射光谱都可以观察到一个明显的透射峰。

界面态声压模拟场分布如图5(a)所示。

(a)：模拟S1中界面态声压场的空间分布。红色虚线表示结构的中心线。色标表示声压归一化幅值。(b)：S1界面态实测声压场用红色圈表示，沿红色虚线的模拟声压场分布用黑色实线表示。振幅由P0的最大值归一化。

 从图5(b)可以观察到，界面态的声压分布在离界面结(x= 0)远的地方呈指数衰减。

---

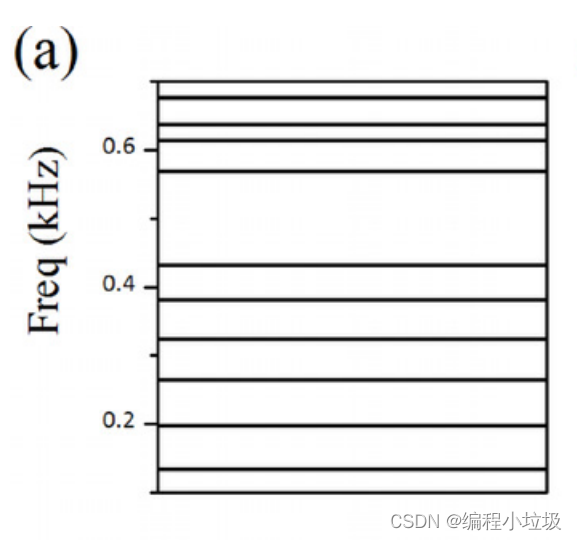
拓扑非平凡声子晶体末端的拓扑边缘态，如图6(c)所示，PC1的第一个带隙没有出现边缘状态，因为该结构具有拓扑平凡几何Zak相位(0)。相反，拓扑边缘态(红线)出现在图6(d)中0.516 kHz处PC2的第一个带隙中，因为该结构具有拓扑非平凡几何Zak相位(p)。

图6所示。(a)声子晶体由29个a单元组成，称为PC1。(b)声子晶体由29个单元b组成，称为PC2。注意，标记为蓝色的谐振器是为可能的边缘状态提供类似声学环境的附加谐振器。(c) PC1的模拟本征频谱如(a)所示。(d) PC2的模拟本征频谱如(b)所示。通过比较，在0.516 kHz处(d)出现了两个用红线标记的简并边缘状态。(e) (d)中红线对应的声压场分布。两者的声压场都局限在边缘附近。色标表示声压归一化幅值。

可以看出，无论终端谐振腔如何摄动，PC1的第一带隙中都没有出现边缘态。相反，对于PC2，第一带隙中拓扑边缘状态的存在对摄动具有鲁棒性。