序列的Z变换和逆Z变化

序列的Z变化针对的是非周期发散的序列或者收敛性不确定的序列,序列x(n)的双边z变换为n从负无穷到正无穷对x(n)*z的-n次方求和，单边z变换是n从0到正无穷求和的。即就是X(z)=Ex(n)z-n。
z变换的存在条件是级数绝对可和，也就是X(z)的模小于无穷大，满足这个等式的z的取值范围就是收敛域

X(z)还可以表示为P(z)/Q(z)，其中分子等于0时的z值就是零点，而分母等于0时的z值是极点，我们一般通过极点的取值来求X(z)的收敛域

z变化与傅里叶变化的联系是X(exp jw) = X(z)当z=exp jw的值
当z = exp jw时，我们对其求模，发现它恒等于1，所以当X(z)的收敛域包含单位圆上的点时，该z变化存在傅里叶变化

例题：已知x(n)=u(n),求x(n)的z变化
直接带入定义式，记住求和上下限要改成0到正无穷，最后在利用等比数列求和公式就可以了,我们要让这个式子的绝对值小于无穷大，所以必须公比小于1，最后算出来结果是|z|>1，很明显这不包含单位圆，所以x(n)的傅里叶不存在，实际上我们也可以用之前的知识得出要想x(n)的傅里叶变化存在，则必须满足绝对可和条件.
最后我们得出结论：一个序列的傅里叶变化不存在，但是在一定的收敛域内是存在z变换的

接下来我们来研究不同序列的z变化，总共研究4种序列的z变化
1.有限长序列
有限长序列从名字上就很容易明白，我们分三种情况，分别是两个同时小于0，同时大于0，一个小于0另一个大于，请见书上49页下，其中当都大于0的情况下这个有限长序列又叫因果序列
2.右序列
右边可以趋于无穷，但左边不能
右序列要分两种情况讨论，当n>0时和上述那个一样，是一个因果序列，因果序列的z变化的收敛域是圆外所有
当n<0时，我们把其拆为左加右形式，再利用有限长序列性质和因果序列的性质就可以得出来，这在书上50页
3.左序列
左序列依然分两种情况，左序列又叫反因果序列，它的z变化的收敛域是圆内
4.双边序列
双边序列就是左序列加上右序列的，求它的收敛域其实就是分别求左和右序列的收敛域，然后求交集就可以了
一般情况下，左序列的n要小于0，右序列的n要大于0
例题:求x(n)=a的|n|次方的z变化
直接带入定义式，由于带有绝对值，我们把绝对值先去掉，去掉绝对值后注意求和号的上下限，我们把它分为两个，每一个的公比必须小于1，所以得到两个z的用a表示的取值范围，要想二者存在交集，必须|a|小于1。

以上我们学的是正z变化，也就是已知x(n)，求z变化X(z)和收敛域，现在我们来学习已知X(z)和收敛域如何反过来求x(n)，书上共介绍了三种方法，分别是留数定理法，幂级数展开法和部分分式展开法
1.留数定理法
第一步：求F(z) = X(z)*z的n-1次方
第二步：构造曲线c，c必须满足三个条件，首先要闭合，还要位于收敛域内，最后还要包围z=0
第三步：寻找F(z)的极点
第四步：若极点是一阶，使用留数定理；若极点是n阶，使用留数辅助定理
留数定理在书上51页下面，留数辅助定理就是书上52页中上，它是求c外各留数之和的相反数.
请看例题：书上52页中间
按照上述过程进行做，先求F(z)，也就是把X(z)乘以z的n-1次方，因为题目中说明了|z|>a,所以我们在半径为a的圆外任意画一条满足上述三个条件的任意图形，然后由于n的正负不确定，所以当n>0时，极点z=a，这是一阶极点，当n<0时，分子的z的n次方写到分母中了，所以极点成了0和a，这是二阶极点，注意极点的阶数不是根据极点的个数来判断的，是根据F(z)来判断的。现在先针对n>0时使用留数定理，直接套公式就可以了，当n<0时，我们用留数辅助定理来做，由于留数辅助定理针对的是c外极点的留数，而我们所画的c它已经包含了0和a这两个极点，所以c外极点数为0，所以值是0。

上述那个题已经提前给出了z的收敛域，但是有些题没有给出收敛域怎么办？
对于这种情况我们先算出X(z)的收敛域，要算收敛域首先就要知道极点，而很多情况下X(z)的极点不止一个，这是就存在收敛域可能有多个，我们就要分别分类讨论。

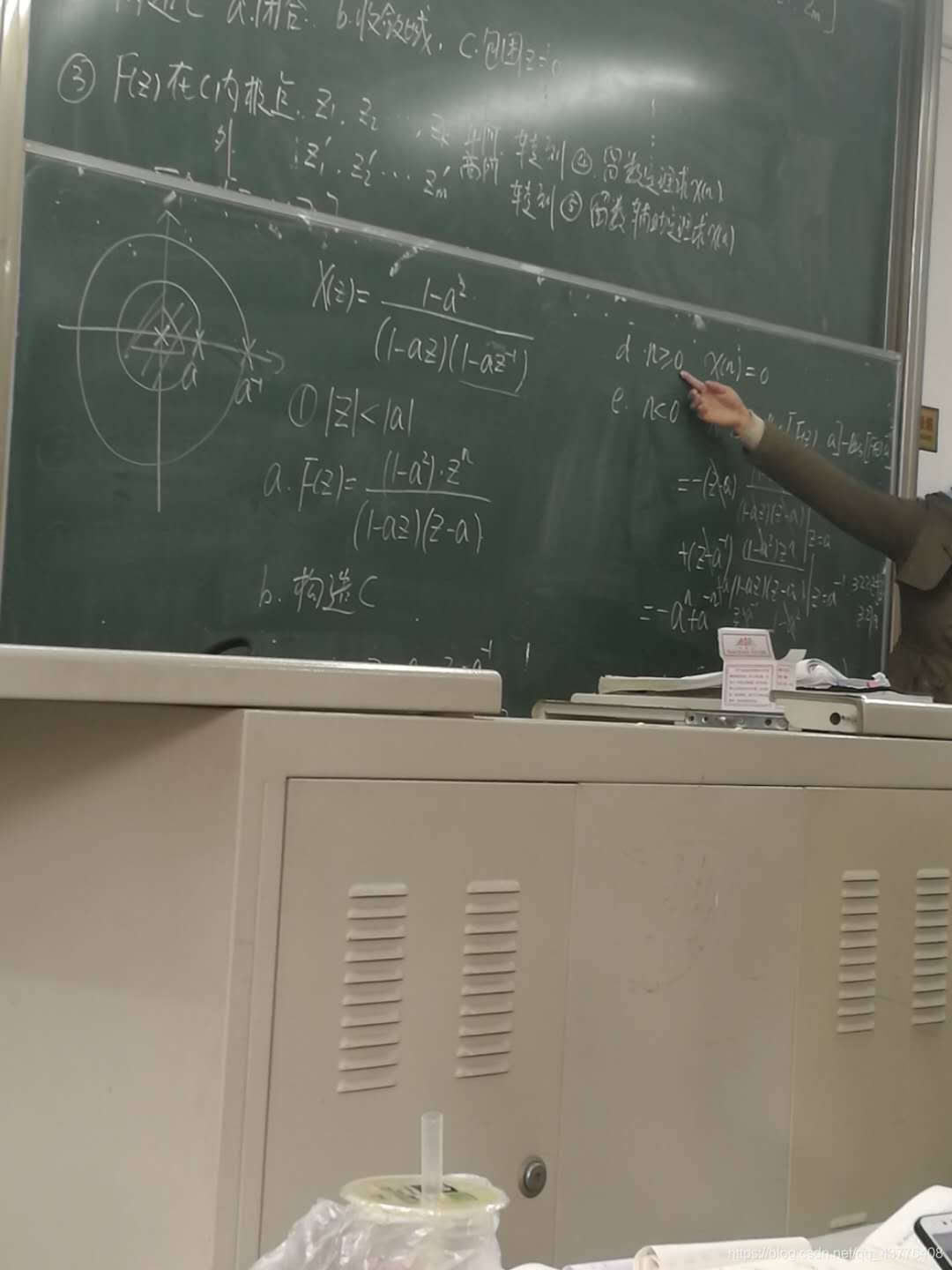
2.幂级数展开法
先把X(z)用定义式展开，你会得到比如X(0），X(1)等等，然后你在把题中给的X(z)的分子除以分母又得到一个多项式，把这个多项式和上一个多项式比较，从而根据规律就可以得出结论
这个方法的难点就是怎样进行两个多项式相除，假设多项式甲除以多项式乙，先用甲的第一项除以乙的全部，你要想法设法消去甲的第一项，也就是结果的第一项乘以乙再减去甲的，这时甲的第一项没了。下来在把减下来的结果的第一项想法设法消去，以此类推，多项式除法的结果是无穷无尽的，最后把你的得到的结果和X(z)用用定义式展开的结果比较在注意一下上下限(可能要过最后的结果乘以u(n)等等）就可以了。
3.部分分式展开法
这个方法比较局限，只适合可以因式分解的和极点是一阶的
对于满足上述两个条件的式子我们对其除以z,然后把结果化为分子分母都是正的z次幂，对分母因式分解，通过书上56页中上两个公式求出系数A1和A2，这样我们就求出了X(z)/z的式子，然后又根据收敛域(题目没有给出收敛域的话你就自己求)以及书上57页z变化公式从而可以很容易得出x(n)的表达式。