目录
一、功能连接分析的基本原理
什么是功能连接?
- 1、电极与电极(或脑区与脑区)之间信号的统计学关系
- 是功能层面的联系而不是结构层面的连接
- 意思是,即使两个电极或者两个脑区之间的功能层面的联系很强,也并不能说明这两个脑区之间存在神经元(结构层面),将这两个脑区连在一起。
- 是功能层面的联系而不是结构层面的连接
- 电极与电极的功能连接:头皮层面完成
- 脑区与脑区的功能连接:必须先要借助源定位技术得到每个脑区的激活,进而分析脑区间的功能连接
- 皮尔逊相关系数:最简单的功能连接指标
- 皮尔逊相关系数用于脑电研究的局限性:(1)有负值:如何解释负相关???? (2)不能提供频域信息,不能告知每个频段的相关性大小;(3)只能描述线性相关性
- 2、方向性:
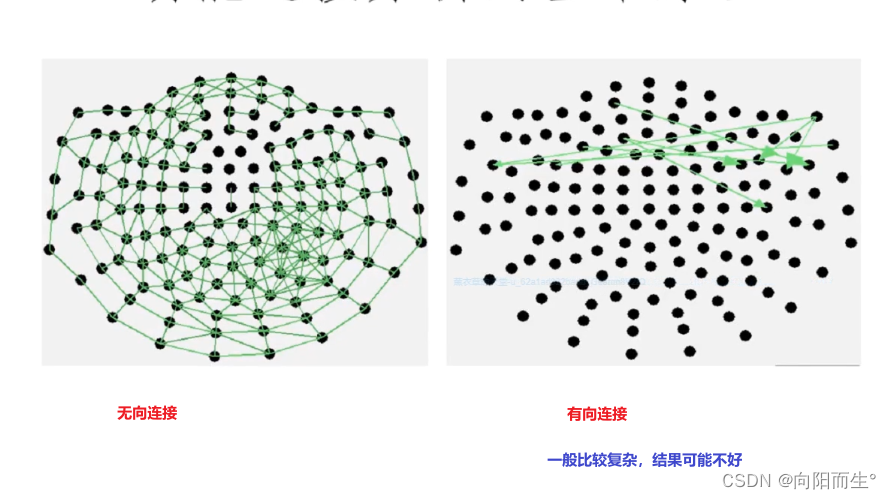
- 无向的功能连接(functional connectivity)
- 有效性连接、效应性连接,有向,可同时评估脑区之间或者电极之间连接的强弱和连接的方向(谁影响谁,存在一个从一个电极到另一个电极的信息流information flow)
- 无向的功能连接(functional connectivity)
- 有向的功能连接(effective connectivity)
- functional connectivity:无向,仅可评估脑区之间或者电极之间连接的强弱
- 3、时变性
- 功能连接随着时间不断变化
- 比如,有两个电极,在t1时间计算了它们之间的皮尔逊相关系数r1,在t2时间计算了它们之间的皮尔逊相关系数r2。那么r1与r2的结果可能是不一样的。
- ps:结构层面的连接变化是非常缓慢的。
二、共同源问题
什么是共同源问题(common source problem)?
- 1、参考电极的选取
- 参考电极不同,功能连接分析的结果可能就不同
- 2、容积传导效应
- 某一个大脑区域产生的信号会传递到所有头皮电极,(每一个电极收到的信号,是来自所有的激活的大脑区域的电信号的叠加),因此两个电极存在功能连接可能仅仅是因为它们与一个共同的神经信号发生源有关
怎样排除共同源问题的影响?
- 方式一、空间滤波后计算功能连接指标
- 方法1:源定位(溯源分析)后得到各个脑区或者ROI(Region of Interest)的信号
- 优点:从头皮还原到各个脑区,结果更易解释
- 缺点:源定位会有误差(生物学原理真的准确吗?受到很多参数影响:颅骨大小,电极信号质量…)
- 方法2:对头皮各个电极的EEG信号进行空间拉普拉斯变换,得到各个电极的源电流密度(current source density,CSD)
- 优点:源电流密度数值与参考电极无关;仅需要少数的参数或假设即可完成
- 缺点:可能不易显著
- 方法1:源定位(溯源分析)后得到各个脑区或者ROI(Region of Interest)的信号
- 方式二、直接使用头皮脑电计算与容积传导无关的功能连接指标
- PLI/wPLI
三、脑电功能连接的常用指标
1、相干(magnitude squared coherence,简称coherence或COH)
2、基于相位同步(phase sychrony)的指标
3、基于格兰杰因果(Granger causality)的指标
4、基于信息论的指标
5、基于广义同步(generalized synchronization)指标
1、相干(magnitude squared coherence,简称coherence或COH)
相干:用于描述在频率f时,两个电极或脑区的线性相关关系,它可以通过计算两个信号的交叉功率谱和它们各自的功率谱来得到。
流程:
假设想计算维度为chan×time×epoch(chan、time和epoch分别为电极或脑区数目、每个分段的点
数、分段的数目)的脑电数据中电极X和电极Y的相干,流程如下:
- 1、分别对电极X和电极Y的脑电数据进行快速傅里叶变换FFT,得到它们的频域表示(维度:f*epoch)
- 2、计算X电极在每个频率点的功率(功率谱)、Y电极在每个频率点的功率(功率谱)、
- 3、X和Y两个电极在每个频率点的交叉功率谱(两个功率谱相乘)
- 3、将交叉功率谱除以两个电极信号(脑区信号)的功率谱,得到相干值。
一般用于静息态EEG的功能连接分析
- 相干值则表示了两个脑区信号在不同频率下的相互作用和同步性的程度,取值范围是[0 1]
- 在某个频率点,两个电极信号不存在线性相关,则其相干值为0;
- 在某个频率点,两个电极信号完全线性相关,则其相干值为1
- 优点:可以在每个频率点评估两个电极或脑区信号的线性相关关系
- 缺点:(1)仅能评估线性相关关系,而不能评估非线性相关关系(2)受到信号功率或波幅大小的影响(3)容易受到容积传导效应的影响
ps:交叉功率谱
- 交叉功率谱反映了两个脑区信号在不同频率下的相互作用和同步性
- 交叉功率谱通常是通过将两个信号进行傅里叶变换后,将它们的功率谱相乘得到的。
- 如果两个信号之间存在同步性,则它们的交叉功率谱在某些频率上会出现峰值
- (如果两个信号之间存在同步性,它们的频率成分会在某些频率上同时出现,并且它们的相位差会保持相对稳定的状态。这种同步现象会导致两个信号的交叉功率谱在这些频率上出现峰值,表示这两个信号在这些频率上存在较强的相互作用和同步性。),
- 反之则会较低。
- (如果两个信号之间不存在同步性,它们的频率成分会随机地出现在不同的频率上,并且它们的相位差会随机变化。这种非同步现象会导致两个信号的交叉功率谱在不同频率上的值较低,表示这两个信号之间没有明显的相互作用和同步性。)
2、基于相位同步(phase sychrony)的指标
什么是相位同步?
- 相位同步(phase synchronization,PS)指的是,两个相互耦合的神经振荡活动的相位(phase)同步化(即两个活动有一个固定的相位差)
- 相位同步通常使用相位差(phase difference)来衡量两个振荡信号之间的同步程度。
- 当相位差为0时,两个信号完全同步,即相位同步最强;
- 而当相位差为π(或180°)时,两个信号完全反相位同步,即相位同步最弱。

- 相位同步可以通过多种方法进行分析,如相位耦合值(phase coupling value)、相位同步指数(phase synchronization index)等。
- 优点是(理论上)与两个神经振荡活动的波幅无关,而只与相位有关。
- ps:相互耦合:指的是两个或多个系统之间存在的相互影响、相互作用的关系。相互耦合可以是正的(positive coupling)也可以是负的(negative coupling)。
- 正的相互耦合表示两个系统之间的变化趋势是一致的,即一个系统的变化会促使另一个系统的变化,反之亦然;
- 而负的相互耦合则表示两个系统之间的变化趋势是相反的,即一个系统的变化会抑制另一个系统的变化。
相位同步的指标
1)、相位锁值(phase locking value,PLV),在某些文献中又被称为Mean Phase Coherence
2)、相位延迟指数(phase lag index,PLI)
3)、加权相位延迟指数(weighted phase lag index,wPLI)
静息态EEG数据进行PLV/PLI计算的流程:
假设想计算维度为chan*time*epoch(E、T和S分别为电极或脑区数目、每个分段的点数、分段的数目)的静息态EEG数据中,电极X和电极Y的PLV/PLI:
(1)首先需要定义某个感兴趣的频段,比如说alpha(8~12Hz)
(2)分别对电极X和电极Y的脑电数据按照前述感兴趣的频段进行带通滤波
- 过滤出我们想要的频段范围的数据
(3)对滤波后电极X和Y的信号进行希尔伯特变换(Hilbert Transform),并进而提取出每个时间点的相位φx和φy(T*s)
- 假设X电极带通滤波后的信号为X(维度为T×S),可通过如下公式计算其相位φx = angle(hilbert(X))
- 个别文章使用短时傅里叶变换或小波变换提取相位
(4)计算电极X和Y的相位差∆φ = φx - φy ,(T×S)
(5)分别在每个分段上计算该分段的PLV/PLI (T×S)
(6)分段间平均,得到整个数据X和Y电极的PLV/PLI (T维)
注意:每两个电极对两两计算
总结起来,就是 :
带通滤波→希尔伯特变换→求相位→求相位差→求每个分段的PLV/PLI→分段间PLV/PLI平均
- PLV/PLI衡量的是两个电极信号在某个频段的相位差的集聚程度(与分散程度相反)
- 每个两个电极的每个时刻点的的相位差,画在一个圆盘上,有多少个时刻点就有多少条线,该线所指的角度就是该时刻点两个电极之间的相位差。
- PLV的取值范围是[0 1]
- 某个时刻点相位差是0°或者180°,此时刻点相位差,被赋值为0;相位差>0度,此时可相位差赋值为1;<0度,相位差赋值为-1;(排除共同源的问题)
- PLV等于0时,两个电极在某个频段的相位差均匀分布在-π至π的区域内,即没有相位同步;(上图左边)
- PLV等于1时,相位差固定为-π~π内的一个固定值,即完全相位同步(上图右边)
静息态EEG数据进行wPLI计算的流程:



注意如下几点:
(1)静息态EEG信号在计算PLV/PLI/wPLI前做完预处理,并分段(如2秒一段)
(2)在实际研究中,你关心的频段可能有多个,那么上述计算PLV/PLI/wPLI的过程每个频段需要分别跑一次
任务态EEG数据进行PLV/PLI计算的流程:
假设想计算维度为E×T×S(E、T和S分别为电极或脑区数目、每个分段的点数、分段的数目)的任务态脑电数据中电极X和电极Y的PLV/PLI,
(1)首先需要对数据进行时频转换(STFT、DWT/CWT等),得到所有分段存储相位信息的时频矩阵 。
(2)在每个分段,电极X和Y的相位矩阵相减,得到所有分段的相位差矩阵
(3)对S个前述相位差矩阵进行分析。对于每个时频点,计算S个分段在该时频点的相位差(S个相位差)的一致性,得到每个时频点的PLV/PLI

3、基于格兰杰因果的指标
- 基本思想:
- 假设有两个时间序列数据x(t)和y(t),如果我们想预测x(t),我们当然可以利用该变量的之前时刻的数据,即x(1)........x(t-1);
- 但是假如我们在预测x(t)时加入变量y的过去信息,即y(1).......y(t-1),对x(t)的预测更为准确,则可以认为x(t)和y(t)两个变量具有因果关系(y为“因”,x为“果”)或者说存在由y(t)至x(t)的“信息流”。

- 未知参数:
- 上述模型中有个未知参数,即p(模型阶数)。在构建自回归模型前,需要利用AIC/BIC等准则估算出p值,再确定P值大小

- 注意事项:
- 由于我们事先并不知道谁是因谁是果,因此我们不仅需要评估y是不是x的原因,我们还需要评估x是不是y的原因
结合滑动窗口技术和频域转换,我们可以以很高的时间和频率分辨率分析事件相关数据。
- https://github.com/sccn/SIFT/wiki (工具箱)
- 格兰杰因果分析是线性的模型,事实上大脑活动非常复杂,线性模型可能很难去拟合它,以至于格兰杰因果分析模型很可能不适用,需要做出检验。
4、基于信息论的指标
- 最常见的是互信息(mutual information, MI)和转移熵(tranfer entropy,TE)。前者可以衡量两个电极信号的无向的信息联系;后者可以衡量两个电极信号的有向的信息流动(即因果关系)
- 1)、互信息
- 互信息(MI)可以检测通过一个信号的数值而获得的关于另一个信号的信息量的大小,即两个信号共有的信息量的大小。如果x(t)和y(t)两个信号相互独立,则MI = 0;否则,MI >0。MI越大表示两个信号共有的信息量越大
- 1)、互信息
- 2)、转移熵
5、基于广义同步的指标
- 最常用的是Synchronization Likelihood (SL)
- SL的优点是它是一个真正意义上的多变量指标。前面的几个指标只能描述x(t)和y(t)两个信号之间的关联性,但是SL却可以描述x(t)与 y(t)、z(t)等多个信号综合的关联性。
- SL是基于混沌系统分析的指标,需要指定嵌入维度、时间延迟、Theiler window、
- number of nearest neighbours和Pref等参数
- 取值范围:[Pref 1]








 本文详细介绍了脑电功能连接分析的基本原理,包括电极间信号的统计学关系,无向和有向的功能连接,以及时变性的概念。共同源问题,如参考电极选择和容积传导效应,对分析结果的影响也得到了探讨。文中提到了几种常用的脑电功能连接指标,如皮尔逊相关系数、相干、相位同步指标(如PLV/PLI/wPLI)以及基于格兰杰因果和信息论的方法,阐述了它们的优缺点及应用场合。
本文详细介绍了脑电功能连接分析的基本原理,包括电极间信号的统计学关系,无向和有向的功能连接,以及时变性的概念。共同源问题,如参考电极选择和容积传导效应,对分析结果的影响也得到了探讨。文中提到了几种常用的脑电功能连接指标,如皮尔逊相关系数、相干、相位同步指标(如PLV/PLI/wPLI)以及基于格兰杰因果和信息论的方法,阐述了它们的优缺点及应用场合。


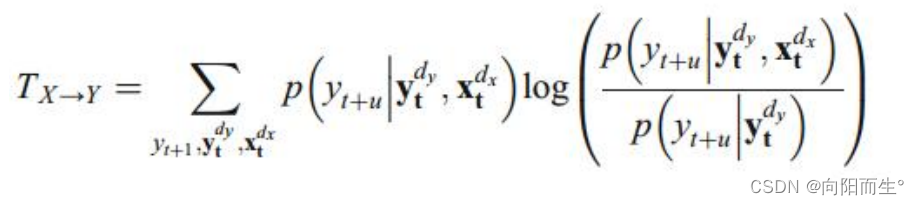
















 747
747

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








