正交矩阵&正交向量

正交矩阵

正交矩阵（Orthogonal Matrix）是指其转置等于其逆的矩阵。

• A^T=A^-1
• 如果A和B都是正交矩阵，并且它们阶数一样，那么AB也是正交矩阵
• |A|=$\pm$ 1

正交向量

• 两个向量的内积如果是零， 那么就说这两个向量是正交的
• 两个向量正交意味着它们是相互垂直的。若向量α与β正交，则记为α⊥β

向量内积

• 两个向量的内积就等于两个向量对应各个维度的分量的乘积的和

我们通常把两个向量的内积写成

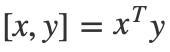
规范正交基

• 如果向量组 e₁,e₂,…,e_r是向量空间V的一个基。
• 如果它们之间彼此正交，那么就称它们是一组规范正交基。

施密特算法求规范正交基

向量空间V中的一组基是a₁,a₂,…,a_r

单位化