目录
论文链接: Digraph Inception Convolutional Networks
摘要
在处理有向图时:
- 直接将有向图转化为无向图来获得拉普拉斯,不仅导致信息传递和聚集出现误差,也剥夺了有向图的结构特征;
- GCN无法获得更多的特征。
针对这些问题,本文提出了DiGCN,将谱卷积进行扩展,并采用k阶近邻获得更大的感受野,学习有向图中的mutil-scale特征。
介绍
以往提出的有向图学习方法
首先,利用图的拉普拉斯分布和PageRank的平稳分布的内在联系,将基于谱的图卷积扩展到有向图
- 有向图不一定满足马尔可夫的平稳分布,基于PageRank传送回每个节点,这种方式导出的拉普拉斯过于稠密,因此引入额外的辅助结点作为每个结点连接的远程端口
- 受到Inception网络的启发,设计可伸缩感受野,可以在一个卷积层中学习到不同大小的特征,避免了由于有向图中的不对称路径而产生不平衡的感受野
有向图卷积
给出基于PageRank的有向图拉普拉斯的定义,并对其进行简化,最后给出有向图卷积的定义。
基于PageRank的有向图Laplacian
对于一个有向图
G
=
(
V
,
E
)
G=(V,E)
G=(V,E),邻接矩阵为
A
A
A,每个结点对应维度为c的特征矩阵
X
X
X,度矩阵(出度)
D
D
D。
根据随机游走,定义有向图的转移矩阵为
P
r
w
=
D
−
1
A
P_{rw}=D^{-1}A
Prw=D−1A,理解为
A
D
\frac{A}{D}
DA。
由于
P
r
w
P_{rw}
Prw不满足不可约性和非周期性(马尔科夫链达到平稳分布的条件),因此需要对该矩阵进行改进。
PageRank
首先需要搞清楚PageRank算法,这里参考PageRank:马尔科夫链
PageRank是Google专有的算法,用于衡量特定网页相对于搜索引擎索引中的其他网页而言的重要程度(百度百科)。PageRank赋予每个网页一个值,值越大,则网页越重要。例如对于下图,结点为网页,边表示链接关系。
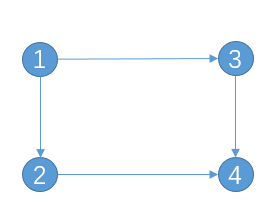
每个点以相等的概率到其它结点,为
1
/
d
1/d
1/d,
d
d
d为出度。例如对于结点1,链接到结点2和3的概率分别为
1
/
2
1/2
1/2。因此对于整个图为
A
/
D
A/D
A/D。
PageRank算法首先给定每个结点相等的初始概率,再经过迭代,得到最终的稳定值。 由于有向图中可能存在只有出度以及只有入度的结点,导致PageRank迭代后得到概率为0的结果:pagerank算法详解
对于只有出度的结点,可以为每个结点添加自循环。即都有一定的概率可以留在当前页面。
对于只有入度的结点,这种结点也称为悬挂结点。当图中存在这样的结点或者存在大量入度的结点时,将容易导致困在该结点走不出去的情况。因此可以假定每个结点都有一定的概率随机跳转到图中的任意其它结点。即为结点添加到其它所有结点的边。
例如对于上图的结点4,添加指向其他结点的边。(图中省略了指向自己的边)

将整个事件分为两种情况:
- B 1 B_1 B1:每个点有 α \alpha α的概率跳转到指向结点
- B 2 B_2 B2:有 1 − α 1-\alpha 1−α的概率跳转到随机结点
因此得到: P = α D − 1 A + ( 1 − α ) 1 N P=\alpha D^{-1}A+(1-\alpha)\frac{1}{N} P=αD−1A+(1−α)N1
至此,关于满足马尔科夫链的平稳分布三个性质已满足:
- 随机性。
- 不可约性。不可约矩阵:方阵A是不可约的当且仅当与A对应的有向图是强联通的
- 非周期性。A为primitive matrix。
Laplacian
根据上述可以进一步得到转移矩阵为:
P
p
r
=
(
1
−
α
)
P
r
w
+
α
n
1
n
×
n
P_{pr}=(1-\alpha)P_{rw}+\frac{\alpha}{n}1^{n\times n}
Ppr=(1−α)Prw+nα1n×n
本文中把
α
\alpha
α称为传送概率。
P
p
r
P_{pr}
Ppr拥有唯一的左特征向量(Perron向量)
π
p
r
\pi_{pr}
πpr
平稳分布
π
p
r
(
i
)
=
∑
i
,
i
→
j
π
p
r
(
i
)
P
p
r
(
i
,
j
)
\pi_{pr}(i)=\sum_{i,i\to j}\pi_{pr}(i)P_{pr}(i,j)
πpr(i)=i,i→j∑πpr(i)Ppr(i,j)
意义为到达顶点
i
i
i的概率,为指向
i
i
i的所有
j
j
j的传入概率之和。由此可知,
π
p
r
\pi_{pr}
πpr性质和无向图里的
D
~
u
\tilde{D}_u
D~u相似,都反映了图的连通性。
得到有向图的拉普拉斯为:
L
p
r
=
I
−
1
2
(
Π
p
r
1
2
P
p
r
Π
p
r
−
1
2
+
Π
p
r
−
1
2
P
p
r
T
Π
p
r
1
2
)
L_{pr}=I-\frac{1}{2}(\Pi_{pr}^{\frac{1}{2}} P_{pr} \Pi_{pr}^{-\frac{1}{2}}+ \Pi_{pr}^{-\frac{1}{2}} P_{pr}^T \Pi_{pr}^{\frac{1}{2}})
Lpr=I−21(Πpr21PprΠpr−21+Πpr−21PprTΠpr21)
其中
Π
p
r
=
1
∣
∣
π
p
r
∣
∣
1
D
i
a
g
(
π
p
r
)
\Pi_{pr}=\frac{1}{||\pi_{pr}||_1} Diag(\pi_{pr})
Πpr=∣∣πpr∣∣11Diag(πpr)
由于这种方式得到的拉普拉斯过于稠密,在进行卷积时计算复杂度较高,因此本文对其进行改进。
Approximate Laplacian
在有向图中添加一个辅助结点,并与图中所有结点建立双向连接,用来代替添加的边
原来的转移矩阵转换为:
P
p
p
r
=
[
(
1
−
α
)
P
~
α
1
n
×
1
1
n
1
1
×
n
0
]
,
P
p
p
r
∈
R
(
n
+
1
)
×
(
n
+
1
)
P_{ppr}= \begin{bmatrix} (1-\alpha)\tilde{P} & \alpha 1^{n\times 1}\\ \frac{1}{n}1^{1\times n} & 0 \end{bmatrix} , P_{ppr}\in R^{(n+1)\times (n+1)}
Pppr=[(1−α)P~n111×nα1n×10],Pppr∈R(n+1)×(n+1)
其中
P
~
=
D
~
−
1
A
~
,
A
~
=
A
+
I
,
D
~
\tilde{P}=\tilde{D}^{-1}\tilde{A}, \tilde{A}=A+I , \tilde{D}
P~=D~−1A~,A~=A+I,D~则为由
A
~
\tilde{A}
A~生成的度矩阵。
如下图中,添加辅助结点5,因此转移矩阵最后一列则表示结点选择事件
B
2
B_2
B2,转移矩阵最后一行表示随机跳转到其它结点概率。

P
p
p
r
P_{ppr}
Pppr同样满足马尔科夫链的三个性质,其有唯一的左特征向量
π
p
p
r
\pi_{ppr}
πppr,特征值为1 。
π p p r = ( π a p p r , π ξ \pi_{ppr}=(\pi_{appr},\pi_{\xi} πppr=(πappr,πξ,其中 π a p p r ∈ R n \pi_{appr}\in R^n πappr∈Rn为前n个点的平稳分布,而 π ξ \pi_\xi πξ为添加的辅助结点的平稳分布。
定理1.当传送概率
α
→
0
\alpha\to 0
α→0时,
π
a
p
p
r
P
~
−
π
a
p
p
r
→
0
\pi_{appr}\tilde{P}-\pi_{appr} \to 0
πapprP~−πappr→0
因此可以将
α
\alpha
α调小,从而得到:
L
a
p
p
r
≈
I
−
1
2
(
Π
a
p
p
r
1
2
P
~
Π
a
p
p
r
−
1
2
+
Π
a
p
p
r
−
1
2
P
~
T
Π
a
p
p
r
1
2
)
L_{appr}\approx I-\frac{1}{2}(\Pi_{appr}^{\frac{1}{2}} \tilde P \Pi_{appr}^{-\frac{1}{2}}+ \Pi_{appr}^{-\frac{1}{2}} \tilde P^T \Pi_{appr}^{\frac{1}{2}})
Lappr≈I−21(Πappr21P~Πappr−21+Πappr−21P~TΠappr21)
其中
Π
a
p
p
r
=
1
∣
∣
π
a
p
p
r
∣
∣
1
D
i
a
g
(
π
a
p
p
r
)
\Pi_{appr}=\frac{1}{||\pi_{appr}||_1}Diag(\pi_{appr})
Πappr=∣∣πappr∣∣11Diag(πappr)
定理2.当传送概率 α → 1 \alpha \to 1 α→1时, Π a p p r → 1 n I n × n \Pi _{appr}\to \frac{1}{n}I^{n\times n} Πappr→n1In×n,此时拉普拉斯矩阵 L a p p r → I − 1 2 ( P ~ + P ~ T ) L_{appr}\to I-\frac{1}{2}(\tilde P+\tilde P^T) Lappr→I−21(P~+P~T)。并且当图为无向图时,此时 L a p p r → I − D ~ − 1 A ~ L_{appr}\to I-\tilde D^{-1}\tilde A Lappr→I−D~−1A~,此时正好为无向图的归一化拉普拉斯。
定理2表明,常用的无向图拉普拉斯为本文方法在某些条件下的特例,可以说 α \alpha α可以作为控制从有向到无向的转换程度。因此, α \alpha α越小,保留的属性越有方向性。
Convolution
根据上述推理,定义了对称的有向图拉普拉斯,并且根据无向图的卷积可以得到有向图卷积为:
Z
=
1
2
(
Π
a
p
p
r
1
2
P
~
Π
a
p
p
r
−
1
2
+
Π
a
p
p
r
−
1
2
P
~
T
Π
a
p
p
r
1
2
)
X
Θ
Z=\frac{1}{2}(\Pi_{appr}^{\frac{1}{2}} \tilde P \Pi_{appr}^{-\frac{1}{2}}+ \Pi_{appr}^{-\frac{1}{2}} \tilde P^T \Pi_{appr}^{\frac{1}{2}})X\Theta
Z=21(Πappr21P~Πappr−21+Πappr−21P~TΠappr21)XΘ
有向图Inception网络
根据相关研究可知,结点的信息是以类似随机游走的方式传播到其它结点的,这表明路径是特征传输的方式,感受野的大小由图中路径的长度决定。
可伸缩感受野
在有向图中,许多路径不是双向的,容易导致有向图中的感受野不平衡。
本文定义了一个有向图的k阶邻近度,能够从k阶相邻结点中提取隐藏信息。如果两个结点共享共同的邻居,那么认为他两是相似的。
对于图
G
=
(
V
,
E
)
G=(V,E)
G=(V,E),若存在
v
i
→
.
.
.
→
v
e
←
.
.
.
←
v
j
v_i{\to ...\to }v_e\gets ...\gets v_j
vi→...→ve←...←vj,称这条路径为
k
t
h
−
o
r
d
e
r
m
e
t
t
i
n
g
p
a
t
h
M
i
,
j
(
k
)
k_{th}-order\ metting\ path\ M_{i,j}^{(k)}
kth−order metting path Mi,j(k)
同理有
v
i
←
.
.
.
←
v
e
→
.
.
.
→
v
j
v_i\gets ...\gets v_e\to ...\to v_j
vi←...←ve→...→vj称为
k
t
h
−
o
r
d
e
r
d
i
f
f
u
s
i
o
n
p
a
t
h
D
i
,
j
(
k
)
k_{th}-order\ diffusion\ path\ D_{i,j}^{(k)}
kth−order diffusion path Di,j(k)
认为
i
i
i与
j
j
j为
k
k
k阶近邻,
e
e
e为第
k
k
k阶共同邻居

这里好像有一个问题:对于上图中的2阶邻居和k阶邻居的定义好像存在冲突,图中的2 edges与k-1 edges冲突。暂时先不管,就当做k-1edges处理
k阶近邻矩阵:
对于一个结点而言:
当
k
=
0
k=0
k=0时,
0
t
h
−
o
r
d
e
r
0^{th}-order
0th−order即表示结点自己;
当
k
=
1
k=1
k=1时,
1
s
t
−
o
r
d
e
r
1^{st}-order
1st−order即表示直接相连的点;
当
k
>
=
2
k>=2
k>=2时,表示为k阶邻居。
上式中的 k = 0 , k = 1 k=0,k=1 k=0,k=1的 P P P不难理解,对于第三个式子首先需要了解有向图邻接矩阵幂的意义:
- 邻接矩阵的幂: A k A^k Ak的第 i i i行第 j j j列,表示从 i i i到 j j j长度为 k k k的路径条数
- (扩展)邻接矩阵与自身转置乘积: A A T AA^T AAT对角线上表示结点 i i i的出度, A T A A^TA ATA对角线上表示结点 i i i的入度。
( P ( 1 ) ) k − 1 ( P ( 1 ) T ) k − 1 (P^{(1)})^{k-1}(P^{(1)^T})^{k-1} (P(1))k−1(P(1)T)k−1表示从i指向j的长度为k的路径,并且将其进行对称化。
i n t e r s e c t ( ⋅ ) intersect(\cdot ) intersect(⋅)代表交集,当两个元素存在交集时,进行加和操作。也就是说,当meeting path和diffusion path同时存在时,才执行运算,否则为0。
设置不同大小的k可以改变卷积的感受野。
多尺度的网络
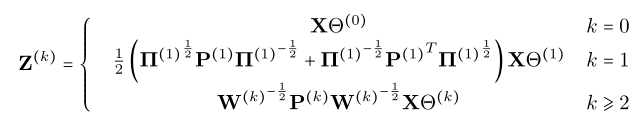
第一行:直接用X进行卷积,直接提取X的特征
第二行:一阶邻居的特征,采用拉普拉斯
第三行:k阶邻居,使用k阶近邻矩阵(这里的w在前文中好像没有出现,文中说其为P的权重矩阵),卷积领域信息
将不同的k分别进行卷积,在将其融合,得到一层的卷积结果:


这是一层训练模型图,将上一层训练输出的Z输入,使用对应的卷积核卷积,再通过融合、激活函数,得到这一层的结果
以上为模型部分,实验部分比较多,也比较复杂, 这里暂且先不写,后续有时间补上

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








