【论文阅读】Two-Phase Hypergraph Based Reasoning with Dynamic Relations for Multi-Hop KBQA

本文仅对文中有关有向超图卷积部分进行介绍

摘要

多跳知识库问答（KBQA）旨在通过跨多个三元组的推理来找到一个因素问题的答案。请注意，当人类执行多跳推理时，人们往往会将注意力集中在不同跳的特定关系上，并确定由该关系连接的一组实体
超图卷积网络（HGCN）可以通过利用超边连接两个以上的节点而不是成对连接来模拟这种行为。然而，HGCN用于无向图，不考虑信息传输的方向。我们引入有向HGCN（DHGCN）来适应具有方向性的知识图。受人类逐跳推理的启发，我们提出了一种基于DHGCN的可解释KBQA模型，即基于动态关系的两阶段超图推理，该模型明确更新关系信息，动态关注不同跳数下的不同关系。此外，该模型逐跳预测关系以生成中间关系路径

有向超图卷积网络

文章参考[Tran et al.,2019]（这篇文章我没找到原文：Loc Tran, Tho Quan, and An Mai. Pagerank algorithm for directed hypergraph. CoRR, abs/1909.01132, 2019.）,提出了有向超图卷积网络。
对于超边$e\in \xi$，在有向超图中被写作$e=(e^{tail},e^{head})$，tail为超边的尾，head为头。因此有两个对应的关联矩阵：
$$h^{tail}(i,j)=\{\begin{array}{ll}1,& v_i\in e_j^{tail}\\ 0,& v_i\notin e_j^{tail}\end{array}$$
$$h^{head}(i,j)=\{\begin{array}{ll}1,& v_i\in e_j^{head}\\ 0,& v_i\notin e_j^{head}\end{array}$$

对应的有四个度矩阵，其中本文利用两个度矩阵：$D_e^{head},D_v^{tail}$
$$D_e^{head}(j,j)=\sum _{i=0}^{|V|}{H}^{head}(i,j)$$
$$D_v^{tail}(i,i)=\sum _{j=0}^{|\xi |}W(j,j)H^{tail}(i,j)$$
参考HGNN的卷积公式，本文提出的卷积公式为：
$$X^{(l+1)}={D_v^{tail}}^{-1}{H}^{tail}W{D_e^{head}}^{-1}{H^{head}}^T{X}^{(l)}P$$
其中$P$为可学习参数，$W$为超边权重，初始化为单位阵，表明超边权重相等都为1

对公式的一点理解：

• $S=W{D_e^{head}}^{-1}{H^{head}}^T{X}^{(l)}$，在聚合前，关联矩阵先与度矩阵$D_e$相乘进行归一化（将超边的信息对每个顶点做平均，平均分配到各顶点）。顶点的特征矩阵$X$与关联矩阵相乘，将信息聚合到指出的超边上
• 再将得到的$S$与${D_v^{tail}}^{-1}{H}^{tail}$相乘，关联矩阵与度矩阵$D_v$相乘进行归一化（将顶点的信息对每条超边做平均），并将前一步聚合得到的信息，再进一步聚合到顶点上

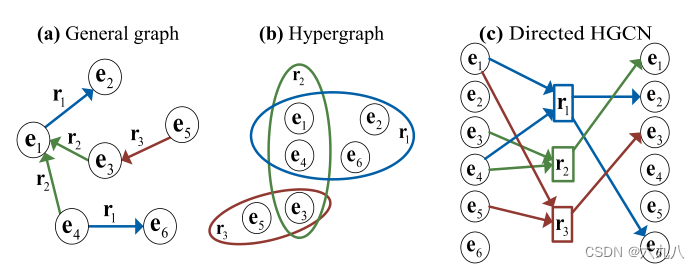
如下图中，图a为普通图，图b为超图，c为本文提出的有向超图。有向超图的卷积过程为顶点e（指出点）的信息聚合到超边r上，再讲超边r的信息聚合到顶点（指入点）上。