数据挖掘之支持向量机SVM以及它的两种解法Maximizing the margin of perceptron

从上节课Margin-Based通理出发，在线性可分linear separable的情况下，我们要找到最大的margin，这样子能使得泛化误差的上界尽可能小，支持向量机Support Vector Machine (SVM) 就是找到最大Margin的方法。

Method1: Optimal Solution

如图所示，先定义了一个使得超平面Margin最大的问题场景

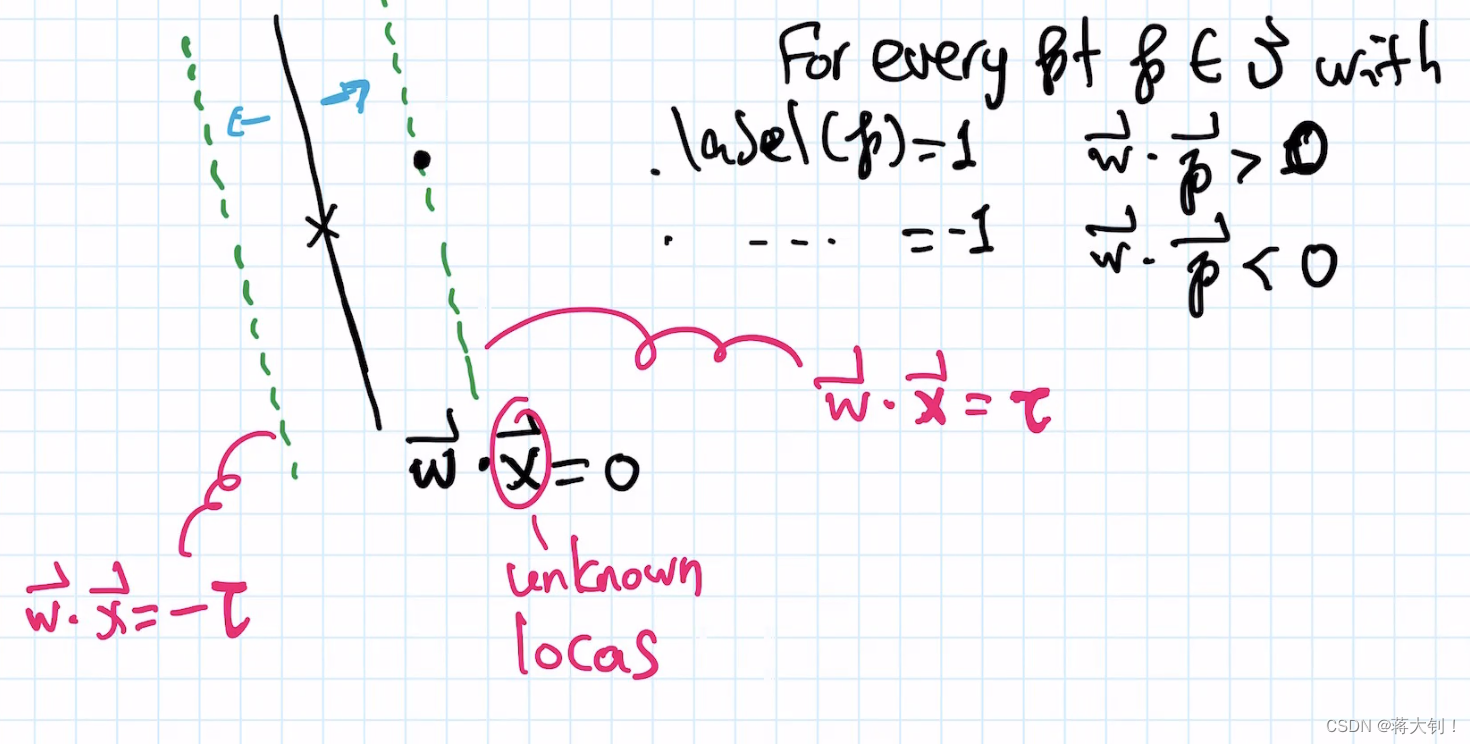
通过标准化$\overrightarrow{w^{\prime }}=\frac{\vec{w}}{\tau }$将$\vec{w}\cdot \vec{x}=\tau$ 转换为了$\vec{w}\cdot \vec{x}=1$的标准形式，同理，通过标准化$\overrightarrow{w^{\prime }}=\frac{\vec{w}}{\tau }$将$\vec{w}\cdot \vec{x}=-\tau$ 转换为了$\vec{w}\cdot \vec{x}=-1$更加有利于后面的公式推导。

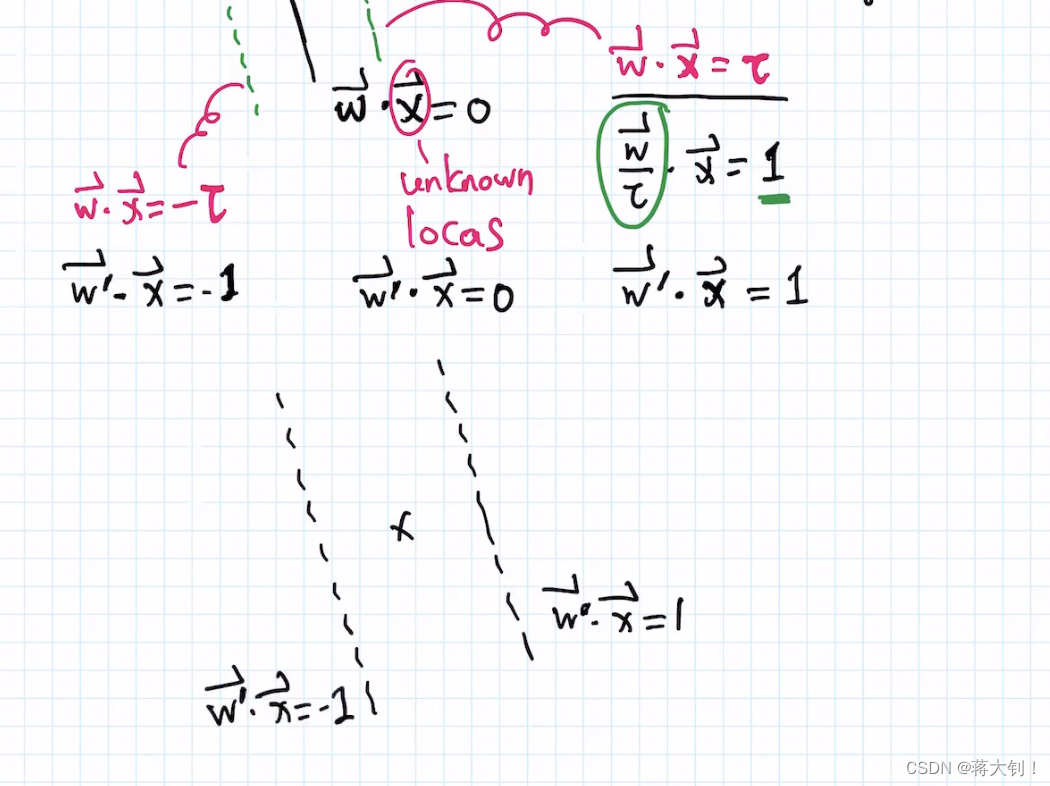
推导公式$margin=\frac{1}{|w|}$如下：
在已经得到$margin=\frac{1}{|w|}$的情况下，为了能够找出最大的margin，其实就是要解决一个二次规划方程quadratic programming, denote ${\vec{w}}^{\prime }=(w_1^{\prime },w_2^{\prime })$：
$$\begin{gathered} minimize|{\vec{w}}^{\prime }| \\ =minimize(w_1^{\prime }{)}^2+(w_2^{\prime }{)}^2 \\ subjectto \\ (w_1^{\prime })\ast p_1+(w_2^{\prime })\ast p_2\ge 1,wherelabel(p)=1 \\ (w_1^{\prime })\ast p_1+(w_2^{\prime })\ast p_2\le -1,wherelabel(p)=-1 \end{gathered}$$
这样子算出来的${\vec{w}}^{\prime }=(w_1^{\prime },w_2^{\prime })$是标准化$\overrightarrow{w^{\prime }}=\frac{\vec{w}}{\tau }$之后的法向量，只是对法向量进行了防缩，并不影响最后找到的分割超平面的斜率情况。

但是解决二次规划方程的时间复杂度过高，尤其是在图中点过于多的情况下，约束方程也有很多，解出答案的效率不高，因此考虑下面的近似解法。

Method2: Approximate Solution

近似解法通过递归的方式尽可能地解出近似于linear separable的最大的margin ${\gamma }_{opt}$ (或者称为${\gamma }^{\ast }$)的值。

该方法蕴含着许多证明，需要尽可能地理解其内涵，incremental algorithm的递归解法也需要进行理解。

Margin Perception引入了一个变量${\gamma }_{guess}$，并基于此进行调整，首先需要保证正负样本能够分开在plane两侧，方法类似于前面的感知机，不过这里为了保证找到最大边界，如果到plane的距离$<\frac{{\gamma }_{guess}}{2}$也是violation point。不违背Margin Perception的点就是满足三个条件：

1. if label of p = 1 and $\vec{w}\cdot \vec{p}>0$
2. if label of p =-1 and $\vec{w}\cdot \vec{p}<0$
3. $|\frac{\vec{p}\cdot \vec{w}}{|\vec{w}|}|\ge \frac{{\gamma }_{guess}}{2}$

当${\gamma }_{guess}$猜测得足够精准，比如${\gamma }_{guess}\le {\gamma }_{opt}$, margin perception就能够在合适的情况下停止并找到符合margin条件的separation plane。需要领会其言外之意，第一层意思是${\gamma }_{guess}\le {\gamma }_{opt}$那么Margin Perception一定会在合适的次数后停止，同时停了也说明${\gamma }_{guess}\le {\gamma }_{opt}$。第二层意思是${\gamma }_{guess}>{\gamma }_{opt}$，该算法就不会自动停止。

实际上，我们猜测${\gamma }_{guess}$并不能十分准确，我们希望它尽可能大且接近${\gamma }_{opt}$但是又不能太大，这就引入了下面的Incremental algorithm. 先猜一个尽可能大的值，然后在递归的过程中用$\frac{1}{2}$不断调整。

其中有几个需要理解证明的点：

1. ${\gamma }_{guess}=R$初始化一定能够保证进行递归，在于一定有${\gamma }_{opt}\le R$，${\gamma }_{opt}$是点到所有分割平面的最大距离，点到separation plane的距离计算公式$|\vec{p}\cdot \vec{u}|=|p\ast u\ast cos\theta |<|p|\le R$，其中$R$是点到原点的最远距离。
2. 每次进行Forced-Termination的时候，对于${\gamma }_{guess}$就将它当作${\gamma }_{opt}$，如果不能在$\frac{12R^2}{{\gamma }_{opt}^2}$下停止，就说明${\gamma }_{guess}>{\gamma }_{opt}$，需要除以2继续重复Line 3.
3. Line 3最终通过self-termination返回的 ${\gamma }_{guess}$不仅小于${\gamma }_{opt}$，而且一定是$>\frac{{\gamma }_{opt}}{2}$的也就是$\ge \frac{{\gamma }_{opt}}{4}$，因为停止的上一次一定${\gamma }_{guess}>{\gamma }_{opt}$才能进入下一轮，到最后一轮停止${\gamma }_{opt}>\frac{{\gamma }_{opt}}{2}\ge \frac{{\gamma }_{opt}}{4}$。

通过以上推论，也可以证明最终Incremental algorithm的执行次数是$O(\frac{R^2}{{\gamma }_{opt}^2})$的。将所有Line3的次数加起来，发现最终只和最后一次最大的的$O(\frac{R^2}{{\gamma }_h^2})$有关，前面的数据根据除以2的关系依次等于$\frac{R^2}{4{\gamma }_h^2}$、$\frac{R^2}{4^2{\gamma }_h^2}$…，又由于${\gamma }_h\ge \frac{{\gamma }_{opt}}{4}$,因此总次数$O(\frac{R^2}{{\gamma }_h^2})$=$O(4\frac{R^2}{{\gamma }_{opt}^2})$.

下面贴上if $${\gamma }_{guess}\le {\gamma }_{opt}$$,margin perceptron terminates in at most $$\frac{12R^2}{{\gamma }_{opt}^2}$$证明相关的通理


claim 3 的证明前提是${\gamma }_{guess}\le {\gamma }_{opt}$的假设。

claim 4直接将$|{\vec{w}}_i|\ge \frac{2R^2}{{\gamma }_{opt}}$代入claim 3进行计算。

claim 5将claim 2和claim 4进行结合使用

将claim 1和claim 5结合使用得到最终结论。

相关题目

1. 题目1.简单地算个点到直线的距离的最小值
   
2. 题目2，3. Margin Perception的近似解法，关键在于找出violation point，其定义我认为首先要满足当label $p=1$，正常的点需要分类器算出来的$w\cdot p>0$（这里就是严格取不到$=$），然后计算distance to the plane $w\cdot p=0$时，其距离可以$>=\frac{{\gamma }_{guess}}{2}$，其中$\frac{{\gamma }_{guess}}{2}$的猜想很重要。

3. 问题4. Margin Perception的最优解法，只需要定义出问题。

4. 问题5，反证法解决证明题。

5. 问题6 Incremental algorithm的推广，将其中的常量系数换成变量。最需要关注的是最后停止的那一轮以及它前面倒数第二轮的数量关系。