鲸鱼优化算法WOA及求解函数应用(含代码，简单易懂)

好好学习0806

已于 2024-03-07 09:03:21 修改

阅读量6.6k

点赞数 11

文章标签：算法

于 2023-09-13 15:12:56 首次发布

本文链接：https://blog.csdn.net/qq_44886972/article/details/132853318

版权

一、介绍

鲸鱼优化算法(WOA)是 2016 年由澳大利亚格里菲斯大学的 Mirjalili 等提出的一种新的群体智能优化算法，其参数量较少，收敛速度很快且容易实现。
鲸鱼优化算法的灵感来源于座头鲸的特殊捕食方式，这种捕食方式被称为“发泡网觅食法”。座头鲸喜欢在靠近水面的位置捕食磷虾和小鱼，座头鲸通过图中所示的圆形或“9”字型路径制造特殊的气泡来完成。研究人员发现了两种与气泡相关的动作，即“向上螺旋”和“双环”。在“向上螺旋”时，座头鲸潜入水底12米左右，开始在猎物周围形成螺旋形的气泡，然后游向水面。而“双环”动作又分为“珊瑚环”、“挑尾”和“捕获环”。

二、数学模型及算法

总体来说，鲸鱼优化算法由三部分动作组成：包围猎物、螺旋攻击猎物（发泡网攻击）、随机搜索猎物。下面分别阐述三种动作的数学模型。

2.1 包围猎物

WOA算法将当前最优候选解做为目标猎物（最优解），在知道猎物位置后鲸群开始根据当前自身与猎物位置的关系更新位置。这种行为用以下公式表示：

$\vec{D}=\left | \vec{C}\cdot \vec{X^{*}}(t)-\vec{X}(t)) \right |$

$\vec{X}(t+1)=\vec{X^{*}}(t)-\vec{A}\cdot \vec{D}$

上述式子中， $t$ 表示当前的迭代次数，而 $\vec{X^{*}}(t)$ 表示在 $t$ 代之前的最优候选解的位置， $\vec{X}(t)$ 和 $\vec{X}(t+1))$ 分别表示 $t$ 代和下一代的解。 $\vec{A}$ 和 $\vec{C}$ 为系数向量，需要单独计算出，其计算公式如下:

$\vec{A}=2\vec{a_1}\cdot \vec{r_{1}}$

$\vec{C}=2\cdot \vec{r_2}$

其中， $\vec{r_1}$ 和 $\vec{r_2}$ 表示两个0到1之间的随机数。 $\vec{a_1}$ 为随着迭代从2线性减小到0的数字表示为：

$\vec{a_1}=2-2*\frac{t}{G}$

其中G表示迭代总次数。

2.2 螺旋攻击

为模拟座头鲸的螺旋过程，也就是发泡网攻击过程，我们在鲸鱼与猎物之间建立一种螺旋方程，模拟座头鲸的螺旋状运动，其公式及示意图如下：

$\vec{D^{'}}=\left |\vec{X^{*}}(t)-\vec{X}(t)) \right |$

$\vec{X}(t+1)=\vec{D^{'}}\cdot e^{bl}\cdot\cos (2\pi l)+\vec{X^{*}}(t)$

其中， $b$ 为常数，一般设为1。 $l$ 为[-1,1]之间的随机数(论文中这样说，但是在WOA公布的源代码中 $l$ 的值和另一个参数 $a_2$ 有联系，我也不确定哪种是对的，或者对结果有什么影响，希望有知道的可以评论区告诉我一下。这里按照源码的公式给出)。

$a_2=-1-\frac{t}{G}$

$l=(a_2-1)\cdot r_3+1$

其中 $r_3$ 为0到1之间的随机数。

包围猎物和螺旋攻击，这两种行为的选择是通过随机的方式选择的，当概率 $p<0.5$ 时选择包围猎物，反之则选择螺旋攻击。其数学表达式如下：

$\vec{X}(t+1)=\left\{\begin{matrix} \vec{X^{*}}(t)-\vec{A}\cdot \vec{D} &,p<0.5 \\\vec{D^{'}}\cdot e^{bl}\cdot\cos (2\pi l)+\vec{X^{*}}(t) & ,p\geqslant 0.5 \end{matrix}\right.$

可以自由调整概率及对应行为，原论文是以0.5为概率。

2.3 随机搜索

随机搜索是WOA中用于全局搜索，跳出局部最优的方式，其数学表示为：

$\vec{D}=\left | \vec{C}\cdot \vec{X_{rand}}(t)-\vec{X}(t)) \right |$

$\vec{X}(t+1)=\vec{X_{rand}}(t)-\vec{A}\cdot \vec{D}$

其中, $\vec{X_{rand}}$ 为随机选择的鲸鱼（解），可以看出，随机搜索的公式和包围猎物的公式很相似，唯一不同的就是方向由当前最优候选解调整为随机一个鲸鱼。包围猎物和随机搜索行为的发生与否取决于 $A$ 的取值，当 $|A|< 1$ 采用包围猎物行为；当 $|A|\geq 1$ 采用随机搜索行为。下面会有流程图，看了流程图应该就清楚了。

2.4 算法流程图

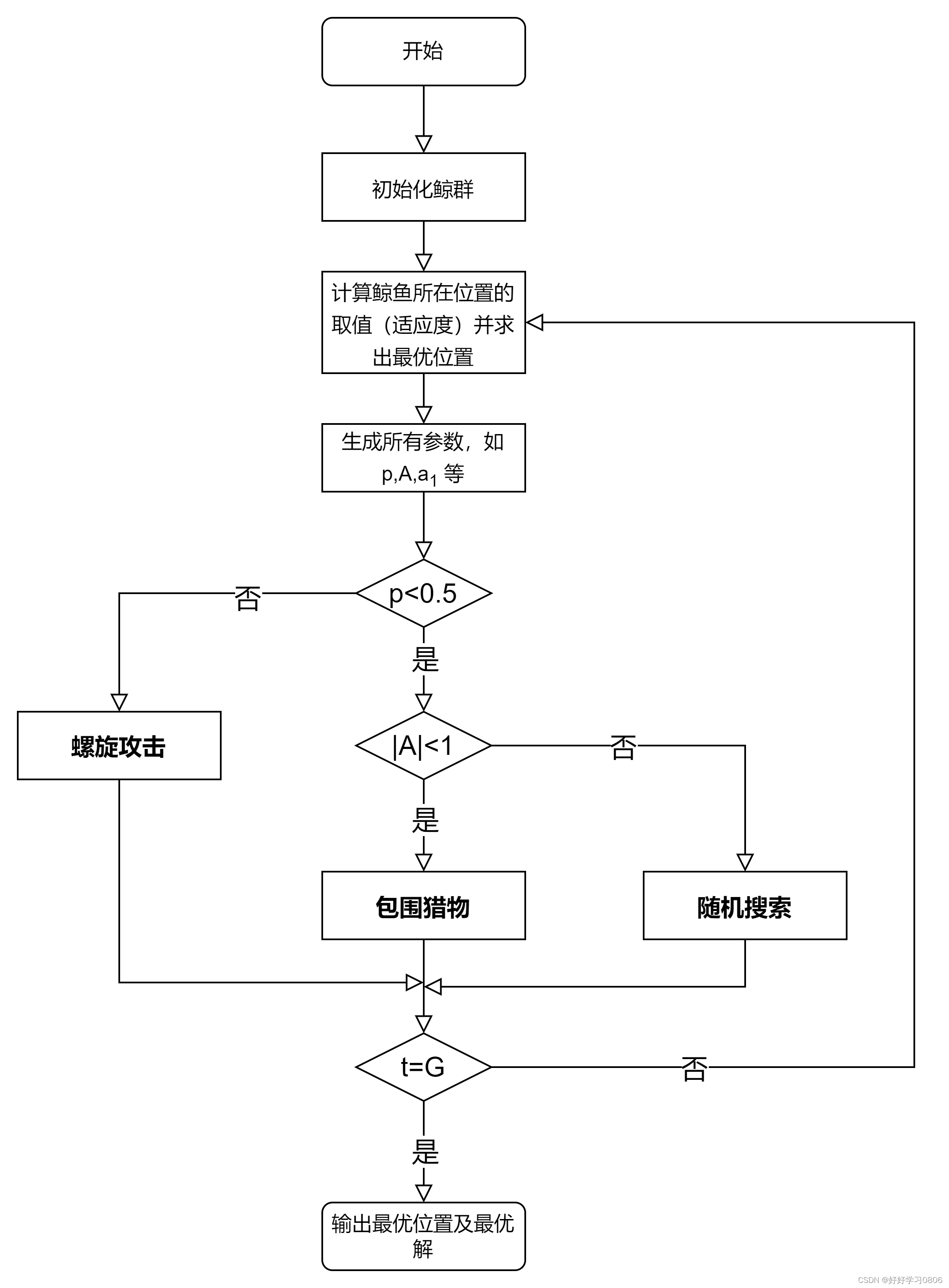
三、求解函数应用

求解二元函数的最大值，函数表达式为：

% 鲸鱼优化算法——WOA
% max f(x1,x2)=21.5+x1*sin(4*PI*x1)+x2*sin(20*PI*x2)
% s.t.    -3.0<=x1<=12.1
%          4.1<=x2<=5.8
clear all
clc
%% 参数列表
whale_num=30;                                           % 鲸鱼数量
dim=2;                                                  % 维度：未知数的数量
G=100;                                                   % 迭代次数
F=@(x1,x2) 21.5+x1*sin(4*pi*x1)+x2*sin(20*pi*x2);       % 待求解函数句柄
up_x1=12.1;                                             % x1的上界
down_x1=-3.0;                                           % x1的下界
up_x2=5.8;                                              % x2的上界
down_x2=4.1;                                            % x2的下界
%% 种群初始化
init_whale_group =[-3.0+(12.1+3.0)*rand(whale_num,1)  4.1+(5.8-4.1)*rand(whale_num,1)];
whale_group=init_whale_group;
% 最优鲸鱼所在位置
whale_max=zeros(G,2);
max_fitness=zeros(G,1);
%% 迭代主体
for t=1:G
    % 超出范围鲸鱼的处理✔
    temp_x1=whale_group(:,1);
    % 小于x1下界的变为下界
    temp_x1(temp_x1<down_x1)=down_x1;
    % 大于x2上界的变为上界
    temp_x1(temp_x1>up_x1)=up_x1;
    whale_group(:,1)=temp_x1;
    temp_x2=whale_group(:,2);
    % 小于x1下界的变为下界
    temp_x2(temp_x2<down_x2)=down_x2;
    % 大于x2上界的变为上界
    temp_x2(temp_x2>up_x2)=up_x2;
    whale_group(:,2)=temp_x2;
    
    % 计算每个鲸鱼的函数值✔
    whale_fitness=zeros(whale_num,1);
    for i=1:whale_num
        whale_fitness(i,1)=F(whale_group(i,1),whale_group(i,2));
    end
    % 记录最好位置✔
    [whale_max_fitness,index_max]=max(whale_fitness);
    if(whale_max_fitness>max_fitness)
        max_fitness(t,1)=whale_max_fitness;
        whale_max(t,:)=whale_group(index_max,:);
    else
        max_fitness(t,1)=max_fitness(t-1,:);
        whale_max(t,:)=whale_max(t-1,:);
    end
    % 计算参数✔
    a1=2-2*t/G;
    a2=-1-t/G;
    
    for i=1:whale_num
        A=2*a1*rand()-a1;
        C=2*rand();
        b=1;
        l=(a2-1)*rand+1;
        p=rand();
        for j=1:dim
            if(p<0.5)
                if(abs(A)<1)
                    % 一、包围猎物✔
                    % 计算移动幅度
                    D=abs(C*whale_max(t,j)-whale_group(i,j));
                    % 按照移动幅度包围猎物（更新位置，即更新一次x1,x2）
                    whale_group(i,j)=whale_max(t,j)-A*D;
                else
                    % 二、随机搜索猎物✔
                    whale_rand_index=floor(whale_num*rand()+1);
                    whale_rand=whale_group(whale_rand_index,:);
                    D=abs(C*whale_rand(j)-whale_group(i,j));
                    whale_group(i,j)=whale_rand(j)-A*D;
                end
            else
                % 三、螺旋运动(发泡网攻击)✔
                D_p=abs(whale_max(t,j)-whale_group(i,j));
                whale_group(i,j)=whale_max(t,j)+D_p*exp(b.*l)*cos(l.*2*pi);
            end
        end
    end
    whale_group;
end

%% 绘图
X=1:G;
plot(X,max_fitness);

运行结果图如下：

可以看出，收敛速度还是很快的，初步学习结束，后续考虑进行鲸鱼算法的多目标应用优化，感兴趣的好兄弟可以标记一下、

好好学习0806

关注

11
点赞
踩
77

收藏

觉得还不错? 一键收藏
10
评论
鲸鱼优化算法WOA及求解函数应用(含代码，简单易懂)

鲸鱼优化算法(WOA)是 2016 年由澳大利亚格里菲斯大学的 Mirjalili 等提出的一种新的群体智能优化算法，其参数量较少，收敛速度很快且容易实现。鲸鱼优化算法的灵感来源于座头鲸的特殊捕食方式，这种捕食方式被称为“发泡网觅食法”。座头鲸喜欢在靠近水面的位置捕食磷虾和小鱼，座头鲸通过图中所示的圆形或“9”字型路径制造特殊的气泡来完成。研究人员发现了两种与气泡相关的动作，即“向上螺旋”和“双环”。在“向上螺旋”时，座头鲸潜入水底12米左右，开始在猎物周围形成螺旋形的气泡，然后游向水面。
复制链接

扫一扫