机器学习理论基础：线代相关、PCA、KKT条件、贝叶斯统计、最大似然估计

李一帆'

已于 2023-11-13 16:41:07 修改

阅读量3.6k

点赞数 13

文章标签：机器学习

于 2022-10-04 21:40:37 首次发布

本文链接：https://blog.csdn.net/qq_44930244/article/details/127163695

版权

本文总结了机器学习理论基础，包括线性代数、PCA、KKT条件、贝叶斯统计和最大似然估计等内容，旨在加深读者对这些关键概念的理解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

机器学习理论基础：线代相关、PCA、KKT条件、贝叶斯统计、最大似然估计

摘要
1.线性代数相关与证明
2.主成分分析
3.KKT条件
4.贝叶斯统计
5.最大似然估计

摘要

本篇博客参考《Deep Learning》的理论基础部分，对线性代数相关与证明、PCA、KKT条件、贝叶斯统计和最大似然估计进行简单总结，以便加深理解和记忆

1.线性代数相关与证明

1.1.线性相关和生成子空间

1.1.1.线性方程组的矩阵表示

考虑m个n元一次方程组成的线性方程组：
$A_{1,1} X_1 + A_{1,2}X_2 + ... + A_{1,n}Xn = b_1 \\ A_{2,1} X_1 + A_{2,2}X_2 + ... + A_{2,n}Xn = b_2 \\ ... \\ A_{m,1} X_1 + A_{m,2}X_2 + ... + A_{m,n}Xn = b_m$
设 $\begin{bmatrix} A_{1,1} & A_{1,2} & ... &A_{1,n} \\ A_{2,1} & A_{2,2} & ... &A_{2,n} \\ & & ... & \\ A_{m,1} & A_{m,2} & ... &A_{m,n} \\ \end{bmatrix} \ \ X= \begin{bmatrix} X_1 \\ X_2 \\ ... \\ X_n \end{bmatrix} \ \ b= \begin{bmatrix} b_1 \\ b_2 \\ ... \\ b_m \end{bmatrix}$

①原线性方程组可以表示为：
$A_{m,n}X_{n,1} = b_{m,1}$

②以行向量分解表示为：
$A_{1:}X = b_1 \\ A_{2:}X = b_2 \\ ... \\ A_{m:}X = b_m \\$

③以列向量分解表示为：
$AX = X_1 A_{:1} + X_2 A_{:2} + ... + X_n A_{:n} = b$

1.1.2.生成子空间

由2中的③可以看出， $A X$ 可以表示为矩阵A的各个列向量的线性组合，这可以看作n个m维向量沿着各自的方向依次走 $X_1,X_2,...,X_n$ 的距离得到的新的向量（拥有m个元素的向量可以看作m维空间中的一个点）

当 $X_i∈R$ 时， $A X$ 所构成的所有向量（点）的集合称为A的这组列向量的生成子空间，也称为A的列空间或A的值域。

由此判断方程组是否有解的从几何上可以看作，b是否包含在A的列空间中，若包含则有解，若不包含则无解。

1.1.3.线性相关

若一组向量中的任意向量都可由其他向量的线性组合表示，则称这组向量线性相关。
反之，若一组向量中的任意向量都无法由其他向量的线性组合表示，则称这组向量线性无关。

从3中生成子空间的角度来看，若A中的某个列向量可以被其他列向量的线性组合表示，则该向量对生成子空间的扩展是没有帮助的，进而它无法为方程组是否有解的问题提供帮助（不过，在方程组有解的情况下，矩阵列向量线性相关影响了解的个数）

1.1.4.方程组通过逆矩阵求解时的考量

逆矩阵的定义： $AA^{-1} = E$ ， $A^{-1}$ 为A的逆矩阵

设A的逆矩阵存在，则对于线性方程组有： $X = A^{-1}b$ ，即方程组很容易通过A的逆矩阵求解，这时解是唯一确定的，因为 $A^{-1}$ 和b都是唯一的确定的。

现在我们考虑什么情况下会使得矩阵A可逆：
由上述分析可知，需要保证X有解且唯一。
1）从X有解考虑：A的列向量为n维，b为m维，若使得对于任意b，X都能有解，则需要保证A的列空间可以包含任意m维向量（这一点保证了A的线性无关的列向量不少于m），这则需要保证A的列空间的维度高于m维，即 n >= m。
2）从X有唯一解考虑，A的列向量应该线性无关，否则在高于m维的空间中会有多种到达b的方程，从代数角度考虑，A的列向量具有多个线性组合可以使方程组有解，因此n = m。

由此可以得出，要想使矩阵A可逆，A一定是一个线性无关的方阵。

当A不是方阵时，也可能有解，但无法通过逆矩阵求解

1.2.证明：通过迹运算描述矩阵的Frobenius范数

1.2.1.概念描述

1）A为m×n型的矩阵
2） $A||_F$ 为矩阵A的Frobenius范数， $||A||_F = \sqrt{ \sum_{i,j}^{m,n}{A_{i,j}^2}}$
3）Tr矩阵的迹：是矩阵各对角线元素之和
4） $A^T$ 矩阵A的转置

1.2.2.证明

$\ \ AA^T_{i,j} = \sum_{k}^{n}{A_{i,k}A^T_{k,j}} \\ ∴ \ \ AA^T_{i,i} = \sum_{k}^{n}{A_{i,k}A^T_{k,i}} \\ ∵ \ \ A^T_{k,i} = A_{i,k} \\ ∴ \ \ AA^T_{i,i} = \sum_{k}^{n}{A_{i,k}^2} \\ ∴ \ \ Tr(AA^T) = \sum_{i}^{m} AA^T_{i,i} = \sum_{i}^{m} \sum_{k}^{n}{A_{i,k}^2} \\ 换k为j，则:\ \ Tr(AA^T) = \sum_{i}^{m} \sum_{j}^{n}{A_{i,j}^2} = \sum_{i,j}^{m,n}{A_{i,j}^2} \\ 则,\sqrt{Tr(AA^T)} = \sqrt{\sum_{i,j}^{m,n}{A_{i,j}^2}} = ||A||_F \\ 原命题得证$

若将A写成更加具体的表示，则通过运算可以更加直观地得到结论

1.3.二元非条件极值充分条件证明

1）二元泰勒展开
$f(x_0,y_0) + f'_x(x_0,y_0)(x-x_0) + f'_y(x_0,y_0)(y-y_0) \\ + \frac {1} {2}f''_{xx}(x_0,y_0)(x-x_0)^2 + \frac {1} {2} f''_{xy}(x_0,y_0)(x-x_0)(y-y_0) \\ + \frac {1}{2}f''_{yx}(x_0,y_0)(x-x_0)(y-y_0) + \frac {1}{2}f''_{yy}(x_0,y_0)(y-y_0)^2 \\ + O(x^{n})$
2）由于f(x,y)具有一阶连续偏导数，再忽略 $O(x^n)$ 大小，由极限的局部保号性，且 $x_0,y_0)$ 为f(x,y)的驻点，得： $f(x_0,y_0) = \frac {1} {2}f''_{xx}(x_0,y_0)(x-x_0)^2 + f''_{xy}(x_0,y_0)(x-x_0)(y-y_0) ) + \frac {1}{2}f''_{yy}(x_0,y_0)(y-y_0)^2$

3）换元
$x_0) \;\;\; Y = (y- y_0) \\ A = f''_{xx}(x_0,y_0) \;\; B = f''_{xy}(x_0,y_0) \;\; C = f''_{yy}(x_0,y_0) \\ f(x,y) - f(x_0,y_0) = \frac {1}{2}AX^2 + BXY + \frac {1}{2}CY^2 = \\ \frac {1}{2}A(X^2 + 2 \frac {B}{A}XY + \frac {B^2}{A^2}Y^2 - \frac {B^2}{A^2}Y^2) + \frac{1} {2}CY^2 = \\ \frac {1}{2} [A(X+ \frac{B}{A}Y)^2 + (C - \frac{B^2}{A})Y^2] = \\ \frac {1}{2A} [A^2(X+ \frac {B}{A}Y)^2 + (AC - B^2)Y^2]$
4）因 $A^2(X + \frac {B}{A}Y)^2$ > 0， $Y^2>0$ ，讨论 $AC-B^2$

$AC-B^2 > 0$ ，是极值点，A > 0 极小值，A < 0 极大值

$AC-B^2 = 0$ 退化成一维情况，无法判断

$AC-B^2 < 0$ ，鞍点，不是极值点

1.4.有关实对称矩阵的几个证明

1.4.1.实对称矩阵

矩阵A为实对称矩阵的定义为：
①A为n阶方阵
② $A_{ij}$ 为实数
③ $A=A^T$

1.4.2.证明一：实对称矩阵的特征值是实数

1）共轭复数

复数
在复数域中，一个复数可以表示为：C = A + Bi，其中A为复数C的实部，B为复数C的虚部
共轭复数
设一个复数C为：C = A + Bi，
则C的共轭复数为： $\overline {C} = A - Bi$
共轭复数的运算特征
和、差、积、商的共轭等于共轭的和、差、积、商

2）证明
对实对称矩阵A特征分解得： $A x = λ x$ ，其中λ为特征值，x为特征值对应的特征向量

现在复数域上考虑，设 $\overline{A}，\overline{λ}，\overline{x}$ 分别为A，λ，x对应的共轭矩阵、向量、复数，其中共轭矩阵和共轭向量表示为 $\overline{A}，\overline{x}$ 中每个元素都是A和x的共轭复数

对共轭矩阵、向量而言： $\overline{A^T} = \overline{A}^T，\overline{x^T} = \overline{x}^T$

因为A为实对称矩阵，易证： $A^T = \overline{A} = \overline{A}^T$

则：
$\overline{x}^TAx = \overline{x}^T\overline{A}x = \overline{A^Tx}^Tx = \overline{Ax}^Tx = \overline{λx}^Tx = \overline{λ}\overline{x}^Tx \;\;\;\;① \\ \overline{x}^TAx =\overline{x}^Tλx = λ\overline{x}^Tx \;\;\;\;② \\ ①-② = 0 → (\overline{λ} - λ)\overline{x}^Tx = 0 \\ \overline{λ} = λ \;\;\;(x ≠ 0) \\ ∴ 在复数域上λ的虚部为0，λ为实数，原命题得证$

1.4.3.证明二：实对称矩阵不同特征值对应的特征向量两两正交

对实对称矩阵A特征分解得： $A x = λ x$ ，其中 $λ_1，λ_2$ 为不同的两个特征值， $x_1,x_2$ 分别为特征值对应的特征向量，则
$Ax_1 = λ_1x_1 → \;x_2^TAx_1 = x_2^Tλ_1x_1 \;\;(左乘x_2^T)\;\;\;① \\ Ax_2 = λ_2x_2 → x_2^TA^T = λ_2x_2^T \;\;(转置)→ x_2^TA^Tx_1 = λ_2x_2^Tx_1 \;\;(右乘x_1)→ x_2^TAx_1 = λ_2x_2^Tx_1 \;\;(A=A^T)\;\;\;② \\ ① - ② → (λ_1-λ_2)x_2^Tx_1 = 0 \\ x_2^Tx_1 = 0 \;\;(λ_1≠λ_2) \\ ∴ x_1，x_2相互正交，原命题得证$

1.4.4.证明三：实对称矩阵n重特征值对应的特征向量子空间为n维的

1）证明：实对称矩阵必可相似对角化

通过数学归纳法证明：
①当n=1时，A本身即是对角阵
②假设n-1阶，A相似于一个n-1阶对角阵
③考虑n阶：

取A的一个特征值 $λ_1$ （由证明二保证），则有： $Aλ_1=λ_1x_1 \;\;\;subject \;to ||x_1||=1$
$x_1$ 可以扩充成n维空间中的一个基，通过施密特正交化、再单位化，可以得到n维空间中的一个标准正交基（ $α_1,α_2,...,α_n$ ）
令 $Q_1=（α_1,α_2,...,α_n）$ ，则有

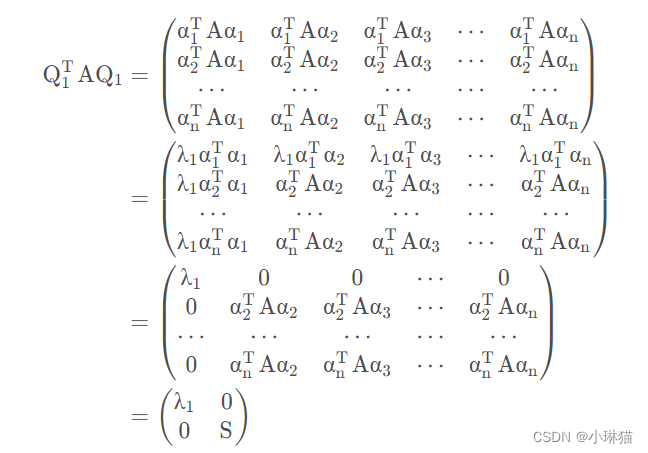
S是n-1阶的实对称矩阵
由②假设得，存在正交阵 $Q_2$ ，有 $Q_2^TSQ_2 = diag(λ_2,λ_3,...,λn)$
令 $Q_3 = \begin{bmatrix}1 & 0 \\ 0 & Q_2 \end{bmatrix}$ ， $Q_3$ 为n阶正交阵，则有
$Q_3^TQ_1^TAQ_1Q_3=(Q_1Q_3)^TA(Q_1Q_3)=diag(λ_1,λ_2,λ_3,...,λn)$
令 $Q = Q_1Q_3$ ，Q是n阶正交阵，则有： $Q^TAQ=diag(λ_1,λ_2,...,λn)$

由①②③归纳得，原命题成立

2）证明：实对称矩阵k重特征值对应的特征向量子空间为k维的

由上证 $A ～ Λ$ ，则 $R (A) = R (Λ) = n$ ，则：
$λE-A \;～\; λE-Λ = diag(λ -λ_1，λ-λ_2，...,λ-λ_n)$

当A的特征值λ取k重根时，diag有k个0，n-k个非零元素，则 $R (λ E - A) = R (λ E - Λ) = n - k$

所以，实对称矩阵k重特征值对应的特征向量恰能构成k维子空间，原命题得证

2.主成分分析

2.1.数据降维

1）简介：机器学习领域中的数据降维是将高维空间中的数据点映射到某个低维空间中，是一种应用广泛的数据预处理方法
2）优点：使数据集更加易用；降低算法开销；去除噪声；使结果容易理解（低维可视化）
3）降维算法举例：主成分分析PCA；因子分析FA；独立成分分析ICA；等距映射；局部线性嵌入

2.2.主成分分析

主成分分析PCA(primary compoments analysis)是一种广泛使用的数据降维算法，其思想是在高维空间中寻找一个低维子空间，用高维空间中数据的低维映射作为降维后的数据表示。

在降维的过程中，我们希望降维后的数据具有更小的损失，也意味着保留尽可能多的信息（这是从数值大小上考量的）

沿着这两种等价的降维目标，主成分分析有两种理论推导方式：最大方差理论；最小化降维造成的损失。这两种思路都能推导出相同的结果，推导过程见5.6节。

2.3.矩阵与向量相乘对向量的影响

本节主要对更好的理解和推导主成分分析提供帮助
$\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} = 1 \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} + 2 \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} + 3 \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}$
$\begin{bmatrix} A_{1,1} & A_{1,2} & A_{1,3} \\ A_{2,1} & A_{2,2} & A_{2,3} \\ A_{3,1} & A_{3,2} & A_{3,3} \\ \end{bmatrix} \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} = 1 \begin{bmatrix} A_{1,1} \\ A_{2,1} \\ A_{3,1} \end{bmatrix} + 2 \begin{bmatrix} A_{1,2} \\ A_{2,2} \\ A_{3,2} \end{bmatrix} + 3 \begin{bmatrix} A_{1,3} \\ A_{2,3} \\ A_{3,3} \end{bmatrix}$
矩阵乘以向量可以看作向量在从原始空间到矩阵列空间的一个映射，相当于将一个向量/坐标轴进行旋转、缩放、高低维度的映射

2.4.最大方差理论

1）思路
在信号处理中认为信号具有较大的方差，噪声具有较小的方差（信噪比是信号与噪声的方差比，越大越好）

沿着这种思路，我们通过旋转坐标轴，在高维空间中寻找一个低维子空间，使得原始数据在新空间相互正交的坐标轴(一组正交基）上的映射尽可能的分散（如下图，相比于紫色坐标轴上的映射，我们更倾向于绿色坐标轴上的映射）

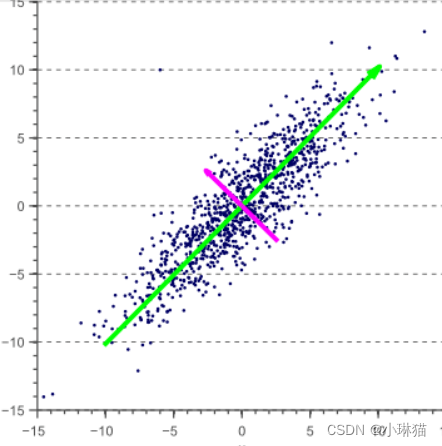
原始数据在新空间坐标轴上的表示即是降维后的新数据表示

2）推导
设样本集合为： $X = \{x_1,x_2,...,x_m\}$
设正交基集合为： $U = \{u_1,u_2,...,u_k \}$
则某一样本点 $x_i$ 在某一基底 $u_j上$ 的投影长度为： $x_i^{T}u_j$ （两向量点积的几何意义）
所有样本点在某基底 $u_j$ 上的方差（目标函数）：
$\ \ D_j =\frac 1margmax \sum_{i=1}^m(x_i^Tu_j -x_{center}^Tu_j)^2 \\ 在数据运算前对数据X进行中心化，即x_{center} = 0 \\ ∴ argmax \ \ D_j =\frac 1m argmax \sum_{i=1}^m(x_i^Tu_j )^2 \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\frac 1m argmax \sum_{i=1}^m(u_j^Tx_ix_i^Tu_j ) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; =\frac 1m argmax \ u_j^T \sum_{i=1}^m(x_ix_i^T ) u_j \\ ∴ argmax \ \ D_j \ \;=\frac 1m argmax \ u_j^T (XX^T ) u_j \\ XX^T是实对称矩阵，必可相似对角化，通过特征分解，得 \\ argmax\ D_j = \frac 1m \ argmax Λ_i$

即，当基底 $u_j$ 为矩阵 $XX^T$ 最大特征值对应的特征向量时，目标函数 $D_j$ 取最大值即为最大特征值。
求出 $XX^T$ 的特征值并按降序排列，其对应的特征向量组成的矩阵U即为编码矩阵（一组正交基），UX即为降维后数据的新表示。

3） $XX^T$ 的意义
在上面的推导中，X是样本每列中心化后的数据，即 $X_{i}=x_{i,j} - x_{center:j}$ ，那么 $XX^T_{i,j}=(x_{i:} - x_{center:j})(x_{:j} - x_{center:i})$ ，即 $XX^T$ 为样本集的协方差矩阵。

4）方法总结
通过以上推导，我们可以得出将原始数据进行主成分分析的一种方法。

对原始数据进行中心化，即每列各个元素减去该列全部元素的均值（这一步实际对矩阵进行了初等变换，可以看作每行元素分别减去各行的1/m）
对中心化后的数据 $XX^T$ 进行特征分解，将特征值降序排序，选择k维最大的特征值对应的特征向量作为新低维子空间中的正交基，组成编码矩阵E。
样本集X与编码矩阵E相乘得到降维后的数据表示

5）示例

原始数据: $X=\begin{bmatrix} -1 & -2 \\ -1 & 0 \\ 0 & 0 \\ 2 & 1 \\ 0 & 1 \end{bmatrix}$
中心化： $X_{center} = \begin{bmatrix} -1 & -2 \\ -1 & 0 \\ 0 & 0 \\ 2 & 1 \\ 0 & 1 \end{bmatrix}$
求协方差矩阵:
$\frac 1 5 X_{center}^T X_{center} =\frac1 5 \begin{bmatrix} -1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} -1 & -2 \\ -1 & 0 \\ 0 & 0 \\ 2 & 1 \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} \frac 6 5 & \frac 4 5 \\ \frac 4 5 & \frac 6 5 \end{bmatrix}$
求协方差矩阵的特征值及对应的特征向量，并将特征向量单位化
$λ_1 = 2 ,η_1 =\begin{bmatrix} \frac {1} {\sqrt 2} \\ \frac {1} {\sqrt 2} \end{bmatrix}$
$λ_2 = \frac 2 5 ,η_2 =\begin{bmatrix} - \frac {1} {\sqrt 2} \\ \frac {1} {\sqrt 2} \end{bmatrix}$
将特征值降序排序，选择k（压缩到k维）个最大特征值对应的特征向量组成编码矩阵 $E=[η_1,...,η_k]$
用原始矩阵与编码矩阵相乘得到映射后的新数据表示（这里取k=1）
$X_{pca} =XE =\begin{bmatrix} -1 & -2 \\ -1 & 0 \\ 0 & 0 \\ 2 & 1 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} \frac {1} {\sqrt 2} \\ \frac {1} {\sqrt 2} \end{bmatrix}=\begin{bmatrix} \frac {-3} {\sqrt 2} \\ \frac {-1} {\sqrt 2} \\ 0 \\ \frac {3} {\sqrt 2} \\ \frac {1} {\sqrt 2} \\\end{bmatrix}$

6）python代码实现

import numpy as np


def pca(_data, k):
    """
    :description: 本方法提供从理论角度通过pca对数据进行降维,应注意数值问题
    :author: LinCat
    :param _data: 输入数据，矩阵
    :param k: 目标降维数
    :return: 降维后的数据，矩阵
    """
    # 数组转矩阵
    origin_matrix = np.mat(_data)
    print('-' * 10, '原始矩阵', '-' * 10)
    print(origin_matrix)
    # 行列数
    row_count = origin_matrix.shape[0]
    column_count = origin_matrix.shape[1]
    # 若所取维数不小于原矩阵维数，则直接返回
    if k >= column_count:
        return origin_matrix
    # 中心化
    center_matrix = origin_matrix
    for i in range(column_count):
        # 列向量
        column_vector = center_matrix[:, i]
        # 求列均值:注意这里直接仍以向量的形式求均值，后续计算时无需显式地迭代计算，使用矩阵计算方法
        column_mean = column_vector.sum(0) / column_vector.shape[0]
        # 该列每个元素减去对应列的列均值
        center_matrix[:, i] = column_vector - column_mean
    print('-' * 10, '中心化后的矩阵', '-' * 10)
    print(center_matrix)
    # 求转置矩阵
    transpose_matrix = center_matrix.T
    # 求协方差矩阵
    cov_matrix = transpose_matrix * center_matrix / row_count
    print('-' * 10, '协方差矩阵', '-' * 10)
    print(cov_matrix)
    # 求协方差矩阵的特征值与特征向量:注意特征值组成的矩阵中特征值按列向量组合
    characteristic_value, characteristic_vector = np.linalg.eig(cov_matrix)
    # 构造特征值与特征向量的字典数组，方便排序
    value_vector_dict = []
    for i in range(len(characteristic_value)):
        value_vector_dict.append({'value': characteristic_value[i], 'vector': characteristic_vector.T[i]})
    # 对数组字典根据特征值降序排序
    value_vector_dict.sort(key=lambda x: x['value'], reverse=True)
    print('-' * 10, '特征值与对应特征向量', '-' * 10)
    for value_vector_item in value_vector_dict:
        print(value_vector_item)
    # 选择k维特征向量组成编码矩阵
    encode_vector = None
    for i in range(k):
        encode_vector = value_vector_dict[i]['vector'] if encode_vector is None else np.vstack(
            (encode_vector, value_vector_dict[i]['vector']))
    print('-' * 10, '编码矩阵', '-' * 10)
    print(encode_vector.T)
    result_matrix = origin_matrix * encode_vector.T
    print('-' * 10, '降维后的矩阵', '-' * 10)
    print(result_matrix)
    return result_matrix


if __name__ == '__main__':
    # 初始数据集：5×2的矩阵，即5组2维数据
    _data = [[-1, -2],
             [-1, 0],
             [0, 0],
             [2, 1],
             [0, 1]]
    pca(_data, 1)

运行结果：

2.5.最小化降维损失

1）思路
将高维空间中的数据有损压缩到一个低维空间，再将其还原到原本的高维空间。我们希望原始数据和压缩还原后的数据（重构数据）之间的损失尽可能的小。

2）寻找编码器
通过编码矩阵E与m维列向量x相乘可以将原始向量从高维空间映射到n维低维空间： $y=E_{n,m} \ x_{m,1}$
通过解码矩阵U与映射后的n维向量y相乘可以将映射后的向量还原到m维高维空间： $x'=U_{m,n} \ y_{n,1}$ ，这里限制解码矩阵U的各个列向量相互正交且都是单位向量。

沿着上面的思路，我们令原始输入向量和重构向量之间的距离（损失）最小：
$E^* = argmin_{E} \; || x- x' ||_2^2 \;\;\;\;\;\;\;\; 平方L2范数 \\ E^* = argmin_{E} \; (x-x')^T(x-x') \;\;\;等价代换 \\ E^*= argmin_E \; x^Tx - x^Tx' - x'^Tx + x'^Tx' \; 分配律 \\ E^* = argmin_{E} \; x^Tx - 2x^Tx' + x'^Tx' \;\; 标量的转置是自己 \\ E^* = argmin_{E} \; - 2x^Tx' + x'^Tx' \;\; 忽略无关项 \\ E^* = argmin_{E} \; - 2x^TUy + (Uy)^TUy = - 2x^TUy + y^TU^TUy \; 代入x'意义 \\ E^* = argmin_{E} \; - 2x^TUy + (Uy)^TUy = - 2x^TUy + y^Ty \; 解码矩阵约束 \\ 令 \;\; ▽_c( - 2x^TUy + y^Ty) =0 \;\;\; 向量微积分 \\ 得 \;\;\; -2U^Tx + 2y =0 \\ 得 \;\;\; y = U^Tx \\ 所以 \;\; E = U^T$
最终我们找到了编码器和解码器的关系，即编码器和解码器互为转置。
重构向量可以表示为： $x' = UU^Tx$

3）寻找解码器
编码器和解码器的关系已知，当我们找到解码器时，编码器也由此而生，寻找解码器时，我们需要考虑全部样本集合，不能再孤立地看待单个样本（向量），必须最小化所有维数和所有点上的误差矩阵的Frobenius范数。为了便于推导，我们约束解码器U为单一单位向量u。
$u^* = argmin_u \; \sum_i || x^i - uu^Tx^i ||_2^2 \\ u^* = argmin_u \; \sum_i ||{x^i} - {x^i}^Tuu^T ||_2^2 \;\; 转置的L2范数不变 \\ u^* = argmin_u \; ||X^T - Xuu^T ||_F^2 \;\; 向量堆叠成矩阵，注意X{i,:} ={x^i}^T\\ u^* = argmin_u \; Tr((X - Xuu^T)^T(X - Xuu^T)) \;\;等价代换 \\ u^* = argmin_u \; Tr(X^TX)-Tr(X^TXuu^T) - Tr(uu^TX^TX) + Tr(uu^TX^TXuu^T) \\ u^* = argmin_u \; -Tr(X^TXuu^T) - Tr(uu^TX^TX) + Tr(uu^TX^TXuu^T) \; 忽略无关项 \\ u^* = argmin_u \; -2Tr(X^TXuu^T) + Tr(X^TXuu^Tuu^T) \; 循环转置 \\ u^* = argmin_u \; -2Tr(X^TXuu^T) + Tr(X^TXuu^T) \; u约束条件 \\ u^* = argmin_u \; -Tr(X^TXuu^T) \; 合并同类项 \\ u^* = argmax_u \; Tr(X^TXuu^T) \; 等价代换 \\ u^* = argmax_u \; Tr(u^TX^TXu) \; 循环转置 \\$
最终化成了同最大方差理论推导一样的形式，通过对实对称矩阵 $X^TX$ 的特征值分解可得，当u取最大特征值对应的特征向量时，上述式子取最大，即最大特征值。当U不限定为一维向量时，令U取k个最大的特征向量对应的特征值即可。

2.6.如何选择降维后的维度

均方误差和 total squared projection error： $\frac 1 m \sum_{i=1}^m || x^i - x'^i ||^2$ ，其中 $x'^i$ 为映射后的值
原数据总量 total variation in the data： $\frac 1m \sum_{i=1}^m || x^i ||^2$
损失比： $\frac {均方误差和} {原数据总量}$

从k=1开始，到k=m为维度，分别计算损失比，直到损失比小于目标值退出循环，如设置损失比 ≤ 0.01，则意味着降维后的数据可以保留99％的数据成分

2.7.scikit-learn PCA

5中按照最大方差理论的方法通过numpy库手写了一遍PCA的实现代码，sklearn库通过SVD分解已经封装了现成的PCA方法，这里给出调用代码，仍使用5中的例子进行对比

# sklearn的PCA
from sklearn.decomposition import PCA
import numpy as np
# 输入数据
X = np.array([[-1, -2], [-1, 0], [0, 0], [2, 1], [0, 1]])
# 映射维度
pca = PCA(n_components=1)
pca.fit(X)
print(pca.transform(X))

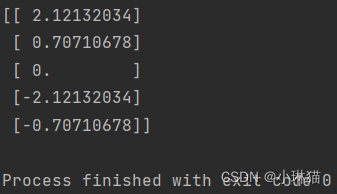
运行结果：

可以看出除了映射后坐标轴的顺序不同，计算的结果是一致的。

3.KKT条件

本章参考国立交通大学周志成老师的线代启示录，主要对不等式约束优化问题中KKT条件进行简要推导

3.1.函数优化问题

1）对于无条件极值问题，可以通过函数极值存在的必要条件寻找极值点（一阶导求驻点、二阶导数测试）
2）对于等式条件极值问题，可以通过引入拉格朗日乘子构造拉格朗日函数，将原问题等价转换为无条件极值问题
3）对于不等式条件问题，由于不等式条件对函数可行域进行了区域的分割，且区域带来了方向性约束，如果想沿着上述的思路将条件极值转为无条件极值，则需要增加更多的约束条件。这时就要用到KKT条件

3.2.KKT条件简介

KKT（Karush-Kuhn-Tucker）条件是针对约束优化的通用方法，它的基础是拉格朗日条件极值，是非线性规划最佳解的必要条件。KKT条件将拉格朗日数乘法所处理的等式约束优化问题推广至不等式。在实际应用上，KKT条件（方程组）一般不存在解析解，许多优化问题可供数值计算选用。

3.3.推导

目标函数为： $f (X)$
不等式约束为： $g (X) \leq 0$ 注意应将不等式写成小于0的形式
引入松弛变量的新目标函数为: $L (X, λ) = f (X) + λ g (X)$

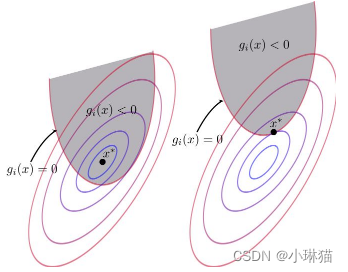
1）互斥松弛性

情况一：最优解处于约束条件内部，这时约束条件是无效的，约束优化问题退化为无约束优化问题，可以将引入的松弛变量λ写为0
情况二：最优解处于约束条件边界上，这时约束优化是有效的，不等式约束问题退化为等式约束问题，可以将约束条件去除不等号，即 $g (X) = 0$

综合上述两种情况可知，无论最优解的位置如何，都满足： $λ g (X) = 0$ ，这称为互斥松弛性

2）对偶可行性

对于上述的情况一，约束条件无需考虑，对于情况二还需要考虑原目标函数与不等式约束函数梯度方向的关系问题，这是因为不等式约束相比于等式约束中，虽然都是在约束边界上进行考虑，但是不等式约束中最佳值的位置是确定的，在约束条件外部，但等式约束中最佳值的位置是不定的，可能在约束边界的任意一侧。

因为最佳值在约束条件外部，因而原目标函数 $f (X)$ 的梯度指向了约束条件内部；
因为不等式约束函数在约束条件中是小于0的，在约束条件外部是大于0的，因而不等式约束函数 $g (X)$ 在约束边界上的梯度指向了大于0的区域，即约束函数的外部。（这里可能会想为什么说约束函数在约束边界两侧是异号的，梯度就指向大于0的一侧？约束函数在小于0的一侧函数值不也可能上升么？这里需要注意梯度是指函数上升速度最快方向上的偏导向量，例如：相同单位长度的变换，相较于-2在约束边界内增至-1，当然没有从-2增至0的上升速度快，因而梯度是指向约束条件外部）

综合上述两点可知，在条件边界上目标函数 $f (X)$ 与不等式约束函数 $g (X)$ 的梯度方向是相反的。

通过令新的目标函数L(X,λ)对X的梯度等于0可得： $L(X,λ)_X = ▽ f(X) + λ ▽g(X) = 0$ ，可得等式： $▽ f (X) = - λ ▽ g (X)$

由于上述推导得: $▽ f (X) ▽ g (X) < 0$ ，所以 $λ \geq 0$

3）综合上述两个额外的条件，再加上引入松弛变量后的新目标函数对X和λ的梯度为0，以及原不等式的约束条件我们便得到了KKT条件方程组。
$_x L = 0 \\ g(x) ≤ 0 \\ λ ≥0 \\ λg(x) = 0 \\$
4）在上述推导的过程中，为了方便起见，我们仅引入了一个不等式约束条件，且没有引入任何等式约束条件。在实际的求解过程中，不等式约束条件和等式约束条件是都可以参与运算且可以有多个的，这里给出一个完整的形式。

目标函数： $argmin\;\;f(x)$
等式约束： $g_i(x) = 0,\;i=1,...,m$
不等式约束： $h_j(x) ≤ 0,\;j=1,...,n$

构造Lagrangian 函数： $L(x,{λ_i},{u_j}) = f(x) + \sum_{i=1}^m λ_ig_i(x) + \sum_{j=1}^n u_jh_k(x)$

KKT条件：
$_x L = 0 \\ g_i(x) = 0,i=1,...,m \\ h_j(x) ≤ 0 ,j=1,...,n \\ u_j ≥0 ,j=1,...,n \\ u_jh_j(x)=0 ,j=1,...,n \\$

3.4.例子

这里给出一个简单示例。
设目标函数为: $f(X)=f(x_1,x_2) = x_1^2 + x_2^2$
设不等式约束条件为： $x_2 <=a$ ，由此可得不等式约束函数为: $g(X) = g(x_1,x_2) = x_2 -a$
设引入松弛变量的拉格朗日函数为： $L(X,λ) = f(X) + λg(X) = x_1^2 + x_2^2 + λ(x_2 -a)$
KKT条件为：
$L(X,λ)_{x_1} = 2x_1 = 0 \\ L(X,λ)_{x_2} = 2x_2 + λ = 0 \\ x_2 ≤ a \\ λ >= 0 \\ λ(x_2-a) = 0$
解得：
$x_1 = 0 \\ x_2 = - \frac 1 2 λ \\ x_2 ≤ a \\ λ >= 0 \\ λ(x_2-a) = 0$
①设λ=0，得：
$x_1 = 0 \\ x_2 = - \frac 1 2 λ = 0 \\ a ≥ x_2 ≥ 0 \\ λ = 0 \\$
②设 $x_2 = a$ ，得：
$x_1 = 0 \\ x_2 = a \\ λ = -2x_2 = -2a \\ λ = -2a ≥ 0 \;\;得，a≤0 \\$
综上①②得：
① a≥0时, X = (0,0)
由下图可以看出，当a≥0时，函数的极值点在约束条件内，所以约束条件失效，极小值在椭圆抛物面的顶点处（黄色点）

② a<0时，X=(0,a)
由下图可以看出，当a≤0时，函数的极值点不在约束条件内，约束条件有效，约束在边界上，极小值X在边界上(0,a)处取（黄色点）

4.贝叶斯统计

4.1.概率论与统计学

简单地说概率论与统计学解决的问题是互逆的。

1）概率论
通过已知的概率模型来精确地计算各种事件发生的结果是概率论。对于概率论来说，每个问题都有唯一的答案，通过相关计算，总可以计算出事件发生的概率。

2）统计学
通过观察的结果来推断模型的不确定性就是统计学，它有许多哲学和艺术的思想在内。

4.2.古典统计学与贝叶斯统计学

古典统计学与贝叶斯统计学的本质区别在于对待未知模型或者模型参数的方法是不同的

1）古典统计学

古典统计学认为未知模型或者模型参数是确定的，只是我们不知道它确切的形式或者取值。
古典统计学通过进行大量重复实验并统计某个特定结果出现的频率作为对未知参数的估计。

2）贝叶斯统计学

贝叶斯统计学认为未知的模型或参数是不确定的随机变量，但这种不确定性可以通过其全概率分布来描述。
特别的，我们首先会根据主观判断或以往的经验对这个概率分布有一个猜测，称为先验分布。然后根据越来越多的观测值来修正对该概率分布的猜测，最后得到的分布称为后验分布。
信念度：贝叶斯统计学中的“概率”的概念可以被解释为我们对未知变量不同取值的信心程度的测度。贝叶斯统计不消除未知变量的不确定性，而是通过越来越多的新的观测点来持续更新我们对于该未知变量不确定性的认知，提高我们对不确定性的判断的信心。
评价：许多实际问题，大量重复实验是不可能的，也就是说我们不具有足够数量的观测数据。在观察数据较小的情况下，对整体参数的估计可能不准，这时增加先验经验是有益的。

4.3.贝叶斯规则

1）条件概率公式: $\frac {p(x,y)} {p(x)}$ ，即在x事件发生的情况下，x，y同时发生的概率是多少
2）贝叶斯规则通过条件概率p(x|y)求条件概率p(y|x)，可以通过条件概率公式推导：
$\;\; p(y|x) = \frac {p(x,y)} {p(x)} \;,\; p(x|y) = \frac {p(x,y)} {p(y)} \\ ∴\;\; p(y|x) p(x) = p(x,y) = p(x|y)p(y) \\ ∴ \;\; p(y|x) = \frac {p(x|y)p(y)} {p(x)}$

4.4.贝叶斯统计

由上述介绍和贝叶斯规则对贝叶斯统计进行推导

1）变量声明

设包含m个观测结果的数据集合为： $X =\{x^1,x^2,...,x^m\}$
设由参数θ控制的该问题的数据生成分布模型为： $P_X(X;θ)$
设参数θ的全概率分布模型（先验分布）为： $P_θ(θ)$

2）循环迭代的思路，让每一个观察结果 $x^i$ 对先验分布进行修正，修正后的每个后验分布作为下一次修正的先验分布

第一次修正的后验分布： $P_θ^1(θ_i|x^1) = \frac {P_X(x^1|θ_i)P_θ(θ_i)} {P_X(x^1)}$ ，若要修正整个 $P_θ(θ)$ ，需要让i取所有值
令第一次修正后的后验分布作为第二次修正的先验概率： $P^1_θ(θ) = P_θ^1(θ|x^1)$
第二次修正的后验分布：
$P_θ^2(θ_i|x^2) = \frac {P_X(x^2|θ_i)P_θ^1(θ_i)} {P_X(x^2)} \\ =\frac {P_X(x^2|θ_i)P_θ^1(θ_i|x^1)} {P_X(x^2)} \\ =\frac {P_X(x^2|θ_i)P_X(x^1|θ_i)P_θ(θ_i)} {P_X(x^2)P_X(x^1)} \\ =\frac {P_X(x^1,x^2|θ_i)P_θ(θ_i)} {P_X(x^1,x^2)} \\$
再重复上述步骤m-1次得： $P_θ(θ_i|x^1,x^2,...,x^m) = \frac {P_X(x^1,x^2,...,x^m|θ_i)P_θ(θ_i)} {P_X(x^1,x^2,...,x^m)}$

3）直接考虑m个观测数据的联合分布概率，可以直接得到上述循环迭代推导的结果：
$P_θ(θ_i|x^1,x^2,...,x^m) = \frac {P_X(x^1,x^2,...,x^m|θ_i)P_θ(θ_i)} {P_X(x^1,x^2,...,x^m)} \\ = \frac {Π_{k=1}^mP_X(x^k|θ_i)P_θ(θ_i)} {\int Π_{k=1}^mP_X(x^k|θ)P_θ(θ) dθ}$

4）通过观察数据修正的后验概率预测新数据
$P_X(x^{m+1}|x^1,x^2,...,x^m) =\int P_X(x^{m+1}|θ)P_θ(θ|x^1,x^2,...,x^m) dθ$

4.5.最大后验估计MAP

贝叶斯统计通过观测数据对参数的先验分布进行修正得到了参数的后验分布，用该后验分布求新样本的分布情况时，是通过参数的全部取值的期望作为模型参数。
最大后验估计则是选择后验概率中具有最大生成可能性的一个参数，是一种点估计：
$θ_{MAP} = argmax_{θ} \;p(θ|X) \\ = argmax_{θ} \;\frac {p(x|θ)p(θ)} {p(x)} \\ ≌\; argmax_{θ}\; p(x|θ)p(θ) \\ ≌\; argmax_{θ}\; logp(x|θ) + logp(θ)$

即可以将最大后验估计分解为logp(x|θ)：标准的似然对数项；logp(θ)先验分布的影响。
相比于全贝叶斯，最大后验估计可以利用先验信息，许多带有正则化项的最大似然可以被解释为近似的MAP估计。
MAP提供了一种直观的方法来设计复杂但课解释的正则化，如更复杂的惩罚项可以通过混合高斯分布作为先验分布得到。

5.最大似然估计

5.1最大似然估计

1）介绍：在总体的分布类型已知的条件下的一种参数估计方法
2）参数估计：根据从总体中抽取的随机样本来估计总体分布中未知参数的过程（点估计、区间估计、点估计的无偏性、有效性、相和性）
3）历史：首先由德国数学家高斯在1821年提出，实则归功于英国统计学家费歇1922

5.2似然与似然函数

1）概率与似然

$p (x; θ)$ ：在已知参数θ时,发生观察结果x可能性大小
$p (θ ∣ x)$ ：在已知观察结果x时，分布函数的参数为θ的可能性大小

2）似然函数： $L (θ ∣ x) = p (x; θ)$

3）例子与解释
概率：设质地均匀的硬币，则抛出两次都是正面的概率为: $P = 0.5 * 0.5 = 0.25$
似然：
抛硬币两次，两次都是正面时，该硬币抛出为正面的概率为0.5的可能性为： $L = 0.5 * 0.5 = 0.25$
抛硬币两次，两次都是正面时，该硬币抛出为正面的概率为0.6的可能性为： $L = 0.6 * 0.6 = 0.36$

如果参数的取值变成0.6的话，结果观测到连续两次正面朝上的概率要比假设0.5 时更大。也就是说，参数取成0.6 要比取成0.5 更有说服力，更为“合理”。
似然函数的重要性不是它的具体取值，而是当参数变化时函数到底变小还是变大。

5.3最大化似然

1）似然最大化
对于似然函数L(θ|x)，对于参数 $θ 1, θ 2$ ，有： $L (θ 1∣ x) = p (x; θ 1) > p (x; θ 2) = L (θ 2∣ x)$

那么意味着，当参数θ为θ1时，原数据生成分布生成x的可能性要大于参数θ为θ2时，原数据生成分布生成x的可能性。
通过不等式的传递性，我们可以得出，在已知总体的模型分布下，对于给定观察结果x，我们希望从所有的模型参数 $θ 1 ， θ 2 ， \dots ， θ n$ 中找出能最大化似然函数的模型参数
2）最大似然估计的定义：

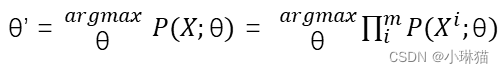
3）求解方法：无条件函数求极值
例子：设质地均匀的硬币，已知模型分布为二项分布，观察结果为{正，正，负}，求模型参数"θ"

计算：
$L(θ|x) = θ * θ * (1- "θ") = θ ^2 (1−θ)，θ∈ [0,1]$
令 $\frac {dL} {dθ} =−3θ^2+2θ=0$ ，得 $θ = 2/3$

5.4最大化对数似然

5.5最大似然估计的一种解释

1）信息论简介

信息论最初提出是为了解决消息设计的最优编码和计算消息的期望长度
将信息论用于机器学习上，主要是描述概率分布或者量化概率分布之间的相似性

2）信息论量化信息(不确定性因素)的一些基本思想

非常可能发生的事件信息量比较少，且极端情况下确保能够发生的事件应该没有信息
较不可能发生的事件具有更高的信息量
独立事件应该有增量的信息

3）一些用于量化信息和量化概率分布的变量
自信息： $I (x) = - l o g (P (x)), x \in [0, 1]$ 单位为奈特(nats)

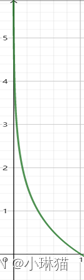
香农熵： $H(X) = E_{(X ~ p)} [I(x)]$ 对整个概率分布中的不确定性总量进行量化
举例：二项分布的香农熵函数： $y = - l o g (ℯ, x) x - l o g (ℯ, 1 - x) (1 - x)$

KL散度： $D_KL(P||P’) = E_{(X~p)} [logP(X) – logP’(X)] = E_{(X~p)} [I_{(P^′ )} (X)−I_{(P )} (X)]$

意义：
早期信息论：计算P编码信息量在P’处的熵则称为交叉熵（来自一个分布的消息用另一个分布的最佳代码传达的平均消息长度）
机器学习应用：量化概率分布之间的相似性
注意：不对称